5274
Apparent diffusion coefficient in the low-frequency limit when measured with oscillating-gradient spin-echo diffusion-weighted imaging1Applied MRI Research, QST, Chiba, Japan
Synopsis
Keywords: Signal Representations, Diffusion/other diffusion imaging techniques, OGSE
The target of oscillating-gradient spin-echo diffusion-weighted imaging (OGSE-DWI) is the spectral density of molecular diffusion, $$$u_2(\omega)$$$, which is predicted to obey a set of asymptotic universality relations that are linked to the global organisation of the sample. In principle, the complex microstructure of a medium can be classified by measuring the spectral density in its low- and high-frequency limits. However, the quantity most often measured with OGSE-DWI is the apparent diffusion coefficient (ADC). It was the purpose of this study to investigate how the low-frequency asymptotic behaviour of the spectral density is reflected in the ADC.$$u_2(\omega)\sim\begin{cases}2D_\infty +c_\infty \omega^\vartheta, & \omega\rightarrow 0\\2D_0-c_0\omega^{-1/2}, & \omega\rightarrow\infty,\end{cases}$$where $$$c_0$$$ is a constant related to the surface-to-volume ratio and $$$\vartheta>0$$$ is a dynamic exponent linked to the random microstructural organisation of the sample. This means that the complex microstructure of a hydrated medium can in principle be classified by measuring $$$u_2(\omega)$$$ in its low- and high-frequency limits. Unfortunately, due to practical limitations on the spectral resolution and range of the technique, it is not possible to directly sample the spectral density with OGSE-DWI. Instead, the quantity most often measured with DWI is the apparent diffusion coefficient (ADC). It is therefore of interest to examine how measurements of the ADC with OGSE-DWI reflect the asymptotic behaviour of $$$u_2(\omega)$$$. As the high-frequency behaviour has been presented in earlier work [3,4], the purpose of this study was to investigate the low-frequency behaviour of the ADC.
Results: An expression for the ADC measured with a single-harmonic cosinusoidal MPG was presented in [5]. If the MPG has finite duration $$$T$$$, finite number of oscillations $$$k$$$ , frequency $$$\omega_k=2\pi k/T$$$ and phase $$$\varphi$$$, the exact relationship between $$$u_2(\omega)$$$ and the ADC measured with OGSE-DWI is [6]
$$ADC_k(\phi)=\frac{1}{2}\int_{a}^{b} \!\!d\omega\ u_2(\omega) H_k(\omega;T,\phi)$$$$H_k(\omega;T,\phi)=\frac{16\pi k^2 T}{1+2\sin^2\phi}\frac{(1-\cos\omega T)[(\omega T)^2\cos^2\phi+4\pi^2k^2\sin^2\phi]}{(\omega T)^2[(\omega T)^2-4\pi^2k^2]^2}.$$Unfortunately, the only way that a single-harmonic MPG can be implemented in practice is when $$$\phi=\pi/2$$$, which means that the only quantity that can actually be measured with pure OGSE-DWI is $$$ADC_k(\pi/2)$$$. Letting $$$\tau$$$ be the timescale characterising the response of a system, the Mellin transform method (MTM) for the asymptotic expansion of integrals [7] was used to show that
$$ADC_k(\pi/2)\sim D_\infty+C_1^\infty(k,\pi/2,\vartheta)\,{\omega_k}^\vartheta+C_3^\infty(k,\pi/2)\,{\omega_k}^5,\qquad\quad\omega_k\tau\rightarrow0.$$
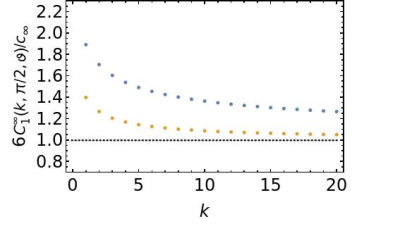
Discussion: Clearly, the dominant asymptotic behaviour of $$$ADC_k(\pi/2)$$$ is qualitatively the same as that of $$$u_2(\omega)$$$ only for $$$0<\vartheta<5$$$. For $$$\vartheta>5$$$, the $$$O({\omega_k}^5)$$$ term will dominate so that the true asymptotic behaviour of $$$u_2(\omega)$$$ is obscured. Figures 1-3 illustrate the behaviour of the coefficient $$$C_1^\infty(k,\pi/2,\vartheta)$$$ with respect to $$$\vartheta$$$ and $$$k$$$ . Many features of the figures can be qualitatively understood using the large $$$k$$$ expansion$$\frac{6C_1^\infty(k,\pi/2,\vartheta)}{c_\infty}\sim 1+\lim_{\vartheta'\rightarrow\vartheta}\{\frac{(\vartheta'-3)\tan(\pi\vartheta'/2)}{2\pi k}+\frac{2\sec(\pi\vartheta'/2)}{\Gamma(2-\vartheta')}(2\pi k)^{-\vartheta'}+O(k^{-\vartheta'-2})\}.$$Overall, when $$$\vartheta>0$$$ the constant term always dominates so that for large $$$k$$$, $$C_1^\infty(k,\pi/2,\vartheta)\,{\omega_k}^\vartheta\sim O(k^\vartheta).$$
Summary: In the low-frequency limit the apparent frequency-dependence of $$$ADC_k(\pi/2)$$$ when plotted against $$${\omega_k}^\vartheta$$$ will tend towards that of the spectral density when $$$0<\vartheta<5$$$. It is therefore likely that structural information can be extracted from the data for samples falling into that range of $$$\vartheta$$$. On the other hand, using pure OGSE-DWI to characterise the structural organisation of a material with a dynamic exponent $$$\vartheta>5$$$ may be challenging. In any case, it is important to remember the $$$k$$$ and $$$T$$$ dependence of the data in the analysis.
Acknowledgements
No acknowledgement found.References
[1] Novikov DS & Kiselev VG, J Magn Reson 210:141-145 (2011).
[2] Novikov DS et al, PNAS 111(14):5088-5093 (2014).
[3] Sukstanskii AL, J Magn Reson 234:135-140 (2013).
[4]Novikov DS et al, NMR Biomed 32:e3998 (2019).
[5] Kershaw J & Obata T, J Magn Reson 326:106962 (2021).
[6] Kershaw J et al, Submitted to Z Angew Math Phys (2022).
[7] Bleistein N & Handelsman RA, Asymptotic expansions of integrals, Dover Publications.
Figures
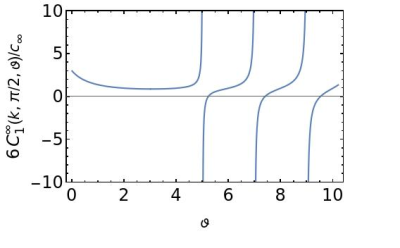
Figure 1. Plot of $$$6C_1^\infty(k,\pi/2,\vartheta)/c_\infty$$$ versus $$$\vartheta$$$ for $$$k=1$$$. The singularities at $$$\vartheta=5,7,9\cdots$$$ reflect the fact that the coefficient resembles $$$1+\tan(\pi\vartheta/2)$$$ for $$$\vartheta>4$$$.
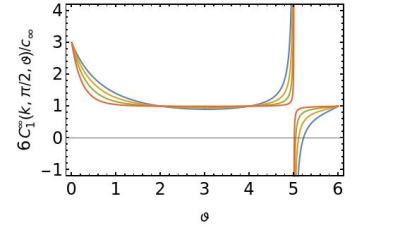
Figure 2. Replot of the region $$$0<\vartheta<6$$$ to show how $$$6C_1^\infty(k,\pi/2,\vartheta)/c_\infty$$$ behaves as a function of $$$k$$$. Curves for $$$k=1$$$ (blue), 2 (orange), 5 (green) and 20 (dark orange) are shown. The coefficient approaches 1 as $$$k^{-\vartheta}$$$ for $$$0<\vartheta<1$$$, as $$$k^{-1}\ln k$$$ for $$$\vartheta=1$$$, and as $$$k^{-1}$$$ for $$$1<\vartheta$$$. Also, $$$6C_1^\infty(k,\pi/2,\vartheta)/c_\infty=1$$$ independent of $$$k$$$ for $$$\vartheta=2,4,6,\cdots$$$.