5273

Principal component subspace reconstruction for compressed sensing of radial quantitative MRI.

Antti Paajanen¹, Olli Nykänen¹, Ville Kolehmainen¹, and Mikko J. Nissi¹
¹Department of Applied Physics, University of Eastern Finland, Kuopio, Finland

Synopsis

Keywords: Sparse & Low-Rank Models, Quantitative Imaging, Image reconstruction

Quantitative MRI offers unique opportunities for compressed sensing reconstructions because the signal evolution is known. Here we compare a principal component subspace reconstruction to a standard total-variation regularized compressed sensing approach with a 3-D radial variable flip angle simulation data. The simulation data allows us to measure only the effect of the chosen reconstruction. The subspace approach consistently yields similar or better image quality and does not seem to require contrast dimension regularization to achieve it.

Introduction

Compressed sensing (CS) has been widely utilized for fast MRI acquisitions while retaining high image quality. One especially advantageous application of CS is quantitative MRI as it offers unique opportunities for compressibility because of its known signal evolution. By simulating the signal evolution over a predetermined parameter range, principal component (PC) analysis can be used to compress the image reconstruction to a low-dimensional subspace, leading to a less ill-posed problem ^1–3.
However, the PC images might not enjoy correlations that are well suited to the widely utilized contrast dimension regularization techniques. The less significant PCs are also of low SNR making it hard to reconstruct them properly in the presence of noise. Both presumably limit the performance of the reconstruction. Additionally, there seems to be no studies where 3-D radial sampling patterns are combined to the subspace approach. Here we study how the total variation regularized subspace and standard CS approaches work with simulated 3-D variable flip angle data.

Theory

The spatially and temporally regularized total variation image reconstruction can be written as
$$\hat{u} = \arg\min_u \{||Au-m||_2^2+\alpha||\nabla_s u||_1 + \beta||\nabla_c u||_1\}, (1)$$ where $$$u$$$ is the contrast image series, $$$m$$$ contains the acquired k-spaces, $$$A$$$ contains the non-uniform fast Fourier transform operators, $$$\nabla_s$$$ is the discrete spatial gradient operator, $$$\nabla_c$$$ is the discrete contrast dimension gradient operator, and parameters $$$\alpha, \beta>0$$$ determine the weighting of the spatial and contrast dimension regularization terms, respectively.
The corresponding subspace reconstruction can be written as $$\hat{w} = \arg\min_w \{||A\Phi_K w-m||_2^2+\alpha||\nabla_s w||_1 + \beta||\nabla_c w||_1\}, (2)$$ where $$$w$$$ is the PC image series and $$$\Phi_K$$$ contains the most significant principal component vectors. Here $$$u\approx\Phi_k w$$$ and the $$$K$$$ is chosen such that $$$||X-\Phi_k\Phi_K^TX||_2 < \epsilon$$$ where $$$X$$$ contains the simulated signal evolutions.
For a simple simulation, the variable flip angle signal equation can be used to form the matrix $$$X$$$ and it reads $$ u = S_0\sin(FA)\frac{1-\exp(TR/T_1)}{1-\exp(TR/T_1)\cos(FA)},$$ where $$$S_0$$$ is the proton density, $$$TR$$$ is the repetition time, $$$T_1$$$ is the longitudinal relaxation time and $$$FA$$$ is the flip angle.

Methods

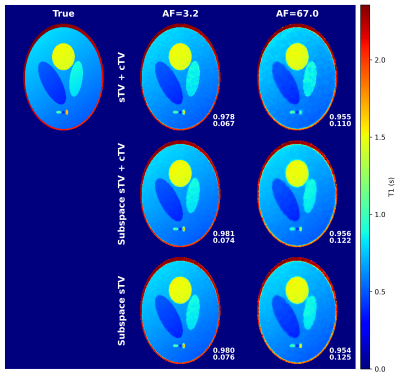
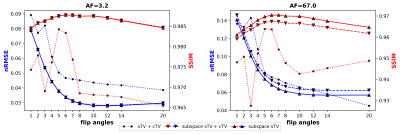
A 3-D Shepp logan phantom ⁴ and a discrete non-uniform Fourier transform were utilized to simulate a radial variable flip angle acquisition (FA = 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14 and 20; TR = 2.9624 ms, image size=256³). All contrast images used unique k-space trajectories. White complex gaussian noise with standard deviation of two percent of the mean absolute noiseless k-space was added to the k-space. The PC basis was formed by simulating 1000 signal evolutions for the chosen flip angles and over the known range of T₁ values. Singular value decomposition was performed and most significant singular vectors were chosen as for them $$$\epsilon=0.007$$$. The optimization problems (1), (2), and (2) without the contrast dimension regularization, titled as “sTV+cTV”, ”subspace sTV+cTV”, and ”subspace sTV”, respectively, were solved with a preconditioned ⁵ primal-dual proximal splitting algorithm ⁶ for acceleration factors (AF) of about 3.2 (63488 spokes/image) and 67.0 (3072 spokes/image). Normalized root mean square error (nRMSE) and structural similarity index (SSIM) ⁷ were used to quantitatively measure image quality.

Results

The subspace approach seems to suffer a bit less from stair-casing, but no major quantitative image quality improvements were gained when compared to the standard approach. Both reconstructions perform well. The standard CS approach achieves the lowest nRMSE values, but worse or similar SSIM scores when compared to the subspace approaches. With the subspace approach, similar performance is achieved with or without the contrast dimension regularization. (Figure 1)
With the contrast image error metrics, the subspace reconstructions yield lower nRMSE values than the standard approach for both AFs, not considering a few outliers. Additionally, the SSIM estimates for the subspace approaches are higher than for the standard one for all flip angles. Overall, the error metrics of the subspace approaches are less erratic. (Figure 2)

Discussion & Conclusions

Principal component subspace reconstruction was studied with a simple quantitative MRI simulation and was found to slightly outperform the traditional CS approach with same regularization terms. The quantitative T₁ relaxation time maps were of similar quality, but contrast image error metrics were consistently better for the subspace reconstructions. Thus, the signal fitting step probably functions as a regularizer of sorts, because same quality T₁ maps are obtained from noisier images for the standard approach. The minimal need for contrast dimension total variation is also logical as the subspace projection works as a contrast dimension sparsifying transform itself. Further, the PC images can be quite different from each other contrast- and SNR-wise and, thus, do not necessarily enjoy well defined correlations between each other, meaning that standard contrast dimension regularization terms can be suboptimal. Indeed, it might be more worthwhile to forego contrast regularization and instead utilize the freed computational power for a more sophisticated spatial regularizer, such as the total generalized variation ⁸.
The subspace approach also enjoys other benefits not visualized here - namely faster convergence and less computational complexity. Both of which are welcome for the large scale 4-D image reconstruction problem. Thus, the subspace reconstruction offers clear benefits over the standard CS approach given that the simulation of the signal evolutions can be performed accurately.

Acknowledgements

This work was supported by the Academy of Finland (grants #285909 and #325146); Academy of Finland, Finnish Centre of Excellence of Inverse Modelling and Imaging (grants #312343 and #336791); Päivikki and Sakari Sohlberg foundation; Jane and Aatos Erkko Foundation; Finnish Cultural Foundation, North Savonia regional fund (grant #65211960), and Doctoral Programme in Science, Technology and Computing of University of Eastern Finland.

References

1. Tamir JI, Ong F, Anand S, Karasan E, Wang K, Lustig M. Computational MRI with Physics-Based Constraints: Application to Multicontrast and Quantitative Imaging. IEEE Signal Process Mag 2020;37:94–104.

2. Tamir JI, Uecker M, Chen W, et al. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn Reson Med 2017;77:180–195.

3. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magn Reson Med 2012;67:1355–1366.

4. Schabel M. 3D Shepp-Logan phantom. Matlab Central File Exchange (https://www.mathworks.com/matlabcentral/fileexchange/9416-3d-shepp-logan-phantom). Retrieved September 2022.

5. Ong F, Uecker M, Lustig M. Accelerating Non-Cartesian MRI Reconstruction Convergence Using k-Space Preconditioning. IEEE Trans Med Imaging 2020;39:1646–1654.

6. Chambolle A, Pock T. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imaging Vis 2011;40:120–145.

7. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing 2004;13:600–612.

8. Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med 2011;65:480–491.

Figures

Estimated T₁ maps for the different reconstruction methods and acceleration factors (AF). Lower right corner of each image displays SSIM (top) and nRMSE (bottom) values. The subspace approaches seem to suffer slightly less from stair-casing, but otherwise the image quality is similar.

The contrast image error metrics for the different reconstruction methods for two different acceleration factors (AF). The subspace approaches consistently yield lower nRMSE and higher SSIM values when compared to the standard CS reconstruction. Additionally, the error metrics behave less erratically.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

5273

DOI: https://doi.org/10.58530/2023/5273