5263
High-Performance FPGA-based Accelerator using Random Projection for pMRI method
Nimra Naeem 1, Omair Inam 2, Abdul Basit 2, Hammad Omer2, and Tayaba Gul2
1Electrical and Computer Engineering, COMSATS University Islamabad, Islamabad, Pakistan, 2COMSATS University Islamabad, Islamabad, Pakistan
1Electrical and Computer Engineering, COMSATS University Islamabad, Islamabad, Pakistan, 2COMSATS University Islamabad, Islamabad, Pakistan
Synopsis
Keywords: Parallel Imaging, Cardiovascular
The random projection method reduces the dimensionality of the data to provide attractive computational advantages in the collection and processing of high-dimensional signals. In literature, it has been successfully applied for the pMRI method i.e., GRAPPA. This paper introduces a very sparse random projection matrix with the same statistical efficiency as dense matrix. The proposed method is implemented on FPGA (working with on-chip processor) device to speed up the GRAPPA reconstruction process. The reconstruction results for in vivo 30 channel human cardiac data set show 6x speed up with little loss in accuracy.Introduction
GRAPPA1 (Generalized Auto calibrating Partially Parallel Acquisition) is a widely used parallel MRI reconstruction technique 3. The processing of data from multichannel receiver coils may increase GRAPPA reconstruction time. Recently, the use of random projections on GRAPPA (RP-GRAPPA)9 has been proposed to reduce the computation costs associated with solving large overdetermined linear equations. Random projection4 can be implemented with linear projection while maintaining the pairwise distances of high-dimensional data with high probability. Based on the principle of distance preservation, Gaussian random matrices and a few sparse {0, +1, -1} random matrices4,6 can be used for random projection. Recently, it has been observed, that the higher memory and processing requirements also limit the efficiency and scalability of GRAPPA and other pMRI techniques on hardware platforms such as FPGAs and GPUs5,7,8 .However, the time complexity of Random Projection also needs to be addressed. In this paper, a new FPGA based accelerator is presented to speed up the process of random projection and offload the computational complexity of GRAPPA. The proposed FPGA based accelerator employs dimension reduction of calibration equations using a highly sparse projection matrix. The proposed accelerator exploits the inherent parallelism of the random projection operations and works in coordination with an on-chip processor to perform GRAPPA reconstruction using multiple receiver coil data. It is demonstrated that randomly projected calibration equations using the proposed accelerator can be highly effective for GRAPPA algorithm in terms of reconstruction time and quality.Method
In this paper, an FPGA-based accelerator is proposed which employs dimension reduction of over-determined linear equations in GRAPPA. GRAPPA reconstruction process has two discrete phases, i.e., calibration and synthesis. During the calibration phase, training datasets are collected in source (S) and target (T) matrices, forming a GRAPPA calibration equation as T = S x W, where the reconstruction coefficients (W) are calculated by pseudo-inverse method i.e., W = ((Sred)H (Sred)-1 ) ((Sred)H (Tred)). This results in complex-valued multiplication of an overdetermined set of linear equations which is computationally expensive. RP-GRAPPA uses pseudoinverse method to solve a reduced set of calibration equations, by the multiplication of source matrix S and target matrix T, with a random matrix R which reduces the higher dimensions down to lower dimensional features as shown in Fig 1. The projection process can be expressed as Tred = R) (T) or Sred = (R) (S).The proposed method uses a highly sparse randomly projected matrix generated with entries {−1, 0, 1} and probabilities { 1/s, 1- 1/s, 1/2s} where s=√(D*λ) , D is a higher dimensional data and a scaling factor ( λ) is introduced for a sparser projection. A slight adjustment in the scaling factor (λ) results in a significant reduction of non-zero Elements as shown in Table 1. Reduction in the number of non-zero elements reduces the time complexity O(kDn) for complex-valued multiplication while estimating the missing weight set in the GRAPPA Calibration phase.
The proposed FPGA-based HW accelerator for Random Projection is implemented using the High-Level Synthesis (HLS) architecture provided by the VIVADO HLS tool 2. The three-phase design flow of the proposed accelerator using the VIVADO HLS tool is shown in Fig 2.
Phase 1: In the first stage, a high-precision float point data type with VIVADO HLS design constraints is used to generate synthesizable source code for Random projection. Consequently, the VIVADO HLS tool generates RTL code for the 32-bit single-precision floating-point FPGA-based Hardware accelerator for Random Projection (HW-ACC-RP).
Phase 2: In this phase, the correctness of the generated RTL is verified using automatic co-simulation feature of VIVADO HLS. The VIVADO HLS tool is used for advanced platform-based RTL transformation, and the synthesizable source code of the Random Projection method employs optimization methods such as:
- "HLS PIPELINE" for data-level parallelism in the Random Projection algorithm
- "HLS UNROLL" for pipelined data processing.
Phase 3: In the final design step, the RTL of the HW-ACC-RP is implemented on a Xilinx FPGA development board as shown in (Fig. 2). It interfaces with the ARM chip GRAPPA processor through the AXI4-stream-interconnect.
Results and Discussion
The experiments are carried out using 30 channel cardiac data set. The data set was under-sampled at different configuration settings. The performance of GRAPPA reconstructions with Random Projection based FPGA is evaluated against single-core and multi-core CPU and GPU with different configuration settings demonstrating fast computation for the proposed method as shown in Table 2. The proposed Random Projection method shows faster reconstruction when compared with conventional methods.Conclusion
The proposed very sparse Random Projection Method for GRAPPA reconstruction allows for substantial reduction in time complexity O(kNd) for complex number multiplication and memory savings without losing reconstruction quality. The experimental results of GRAPPA reconstruction using FPGA-based Random Projection demonstrate a significant reduction in computing time and resource utilization on FPGA. The reconstruction results using in vivo 30 channel cardiac data set shows 6x speed up with little loss in accuracy.Acknowledgements
I am grateful to Medical Image Processing Research Group (MIPRG) at COMSATS University Islamabad, Pakistan, for providing me with a great research environment and computing resources.References
- Griswold, M. A., Jakob, P. M., Heidemann, R. M., Nittka, M., Jellus, V., Wang, J., Kiefer, B., & Haase, A. (2002). Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic resonance in medicine, 47(6), 1202–1210. https://doi.org/10.1002/mrm.10171
- O’Loughlin, D., Coffey, A., Callaly, F., Lyons, D., & Morgan, F. (2014). Xilinx Vivado High Level Synthesis: Case studies. Undefined. https://www.semanticscholar.org/paper/Xilinx-Vivado-High-Level-Synthesis%3A-Case-studies-O%E2%80%99LoughlinCoffey/1981f1f7864f4848f0961e538e51a578fec0ff6f
- Blaimer, M., Breuer, F., Mueller, M., Heidemann, R. M., Griswold, M. A., & Jakob, P. M. (2004). SMASH, SENSE, PILS, GRAPPA: how to choose the optimal method. Topics in magnetic resonance imaging: TMRI, 15(4), 223–236. https://doi.org/10.1097/01.rmr.0000136558.09801.dd
- Ping Li, Trevor J. Hastie, and Kenneth W. Church. 2006. Improving random projections using marginal information. In Proceedings of the 19th annual conference on Learning Theory (COLT'06). Springer-Verlag, Berlin, Heidelberg, 635–649. https://doi.org/10.1007/11776420_46
- Inam, O., Qureshi, M., Laraib, Z., Akram, H., & Omer, H. (2022). GPU accelerated Cartesian GRAPPA reconstruction using CUDA. Journal of Magnetic Resonance, 337, 107175. https://doi.org/10.1016/j.jmr.2022.107175
- Achlioptas, D. (2003). Database-friendly random projections: Johnson-Lindenstrauss with binary coins.
- Inam, O., Basit, A., Qureshi, M., & Omer, H. (2020). FPGA-based hardware accelerator for SENSE (a parallel MR image reconstruction method). Computers in Biology and Medicine, 117, 103598. https://doi.org/10.1016/j.compbiomed.2019.103598.
- Khan, T., Siddiqui, M. F., & Omer, H. (2019). FPGA-Based Pipelined Architecture for Real-Time Estimation of Sensitivity Maps Using Pre-Scan Method in Parallel MRI. Journal of Circuits, Systems and Computers, 29(08), 2050125. https://doi.org/10.1142/s021812662050125x
- Inam, O., Qureshi, M., Malik, S. A., & Omer, H. (2017). Iterative Schemes to Solve Low-Dimensional Calibration Equations in Parallel MR Image Reconstruction with GRAPPA. BioMed Research International, 2017, e3872783. https://doi.org/10.1155/2017/3872783
Figures
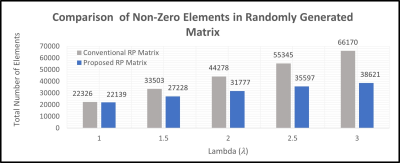
This Graph shows the comparative
analysis of no of non-zero elements in proposed highly sparse random projected
matrix with conventional Random projected matrix
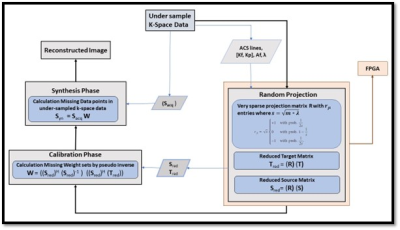
Block Diagram of proposed highly sparse random projection for GRAPPA Reconstruction, Implementation of Random Projection on FPGA for Hardware-based Accelerator.
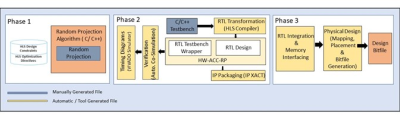
HLS
Design flow for the implementation of proposed Random Projection Method on FPGA.
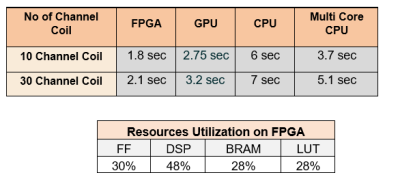
This figure shows Comparative analysis of Computation time of proposed method on different computation platforms such as FPGA CPU, GPU, Multicore CPU with different channel data sets, Other experimental findings demonstrate Resource Utilization when the suggested approach is implemented on an FPGA.
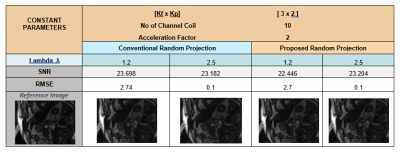
This figure show the change in SNR and RMSE of a 12 coil cardiac data set, In comparison of proposed Random Projection Method with conventional Random Projection Method for various configuration settings.
DOI: https://doi.org/10.58530/2023/5263