5253
Enhancing, Manipulating or Canceling Magnetic Fields in the Distance via Meta Materials for B0-Shimming in Brain MR Imaging1Department of Biomedical Imaging and Image-guided Therapy, Radiology and Nuclear Medicine, Medical University of Vienna, HFMR Centre, Vienna, Austria, 2HFMR Centre, Vienna, Austria, 3Department of Neurosurgery, Medical University of Vienna, Vienna, Austria, 4Institute for Clinical Molecular MRI in Musculoskeletal System, Karl Landsteiner Society, Vienna, Austria
Synopsis
Keywords: Shims, Magnets (B0)
Metamaterials enabling magnetic replicators for $$$B_0$$$ shimming as well as for transcranial magnetic stimulation may overcome traditional methods especially concerning locality of field manipulation, field enhancement or cancellation in the distance in real-time by current tuning.Introduction
Metamaterials are assembled materials exhibiting uncommon physical behavior such as super-lenses1 or magnetic cloaks or concentrators2,3 and described by negative electric/magnetic permittivity/permeability. While the first can be manufactured, the features of the second example can be only emulated, as described below. Rosa Mach-Batlle4,5 demonstrated experimentally that by emulating a negative µ-material the magnetic field in free space can be manipulated (e.g. creating a magnetic dipole field) – without violation of Maxwell’s equations or Earnshaw's Theorem. We propose that this ‘magnetic replicator’ can be applied in MRI, where $$$B_0$$$-inhomogeneities (Figure 1) hamper the imaging quality. $$$B_0$$$-shimming reduces such inhomogeneities, but doesn't change fields only locally. Hence, to goal is to investigate the feasibility of a coil-insert which can generate a $$$B_0$$$ field by mimicking a 'virtual' source inside the object under investigation.Theory and Method
Using Pendry’s transformation optics6,7, for a very long cylindrical, shell like geometry with µ=-1 (Figure 2) Mach-Batlle showed that the magnetic field of an inner, source current inside the shell can be replicated outside of the shell in a specific distance d which is proportional to the shell’s inner/outer radii ratio. A further equivalency was shown: A µ=-1 material can be physically realized by an arrangement of DC-currents spatially oscillating their direction and positioned on the inner and outer surfaces of the shell given by two surface current densities. A second equivalency showed that only one surface current density is necessary, instead of two.To be applied for MRI we addressed the following preliminary questions:
1) For a $$$B_0$$$-inhomogeneity of ~200Hz (e.g. at $$$B_0$$$ = 3T), corresponding to 5mT, can the required magnetic flux density be achieved?
2) What is the optimal geometry of the device for brain MRI? Long shell like structures as previously proposed are unpractical since they only manipulate the field orthogonal along $$$B_{x,y}$$$, but $$$B_z$$$ needs to be changed. Is it possible to revert the direction of the field replication to outside-to-inside to fit a human head?
3) What is the influence of the static magnetic field $$$B_0$$$?
All simulations were performed with COMSOL Multiphysics (magnetostatics module) based on finite-element calculations.
Results
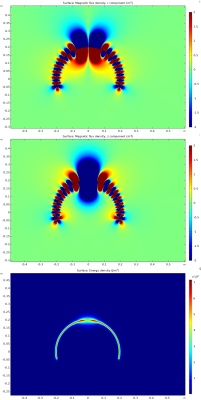
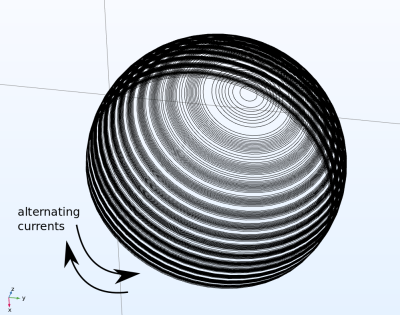
As described in the literature, magnetic field divergencies are created up to the coordinate point were the target field is replicated. This obeys Earnshaw's theorem (no local field maximum in free space). Figure 3 shows exemplary $$$B_y$$$ fields of (from top to bottom): A single current, µ=1 for wire and air; a theoretical µ=-1 shell with an right-centered inner current and an outer $$$B_y$$$ field is replicated on the same position as in the example above; a µ=1 shell with the surface currents as derived in4 and the same inner current mimicking a µ=1 material; a µ=-1 material with an outer current on the right which replicates the $$$B_y$$$ field to the inner shell domain to the left; a µ=1 material with mimicking current replicating the field twice from outer-right to inner-right (weakened) as well as inner-left (weakened) which replicates to outer-left (enhanced) and to the inner shell domain also. The currents for these last case were derived. Figure 4 shows the proposed device in a 2D-z-axisymmetric coordinate system. Only a single surface current density is needed and no outer/inner current was used as proposed in the shell case (last equivalency). Plotted are the $$$B_z$$$ and $$$B_r$$$ fields ranging within the desired order of $$$10^1$$$mT. The replicated field (~1cm apart from the surface) resembles the field of a simple current quite well and similar as the field given in Figure 1. The proposed spherical device geometry (Figure 5) consists of currents along rings with alternating direction, with a surface current density distribution J given by$$$\vec{J}_{\phi}(z)=I/\pi/R\sum_{n=1}^N(d/R)^n cos(n z) \vec{e}_{\phi}$$$
d=-21cm (controlling parameter proportional to replica position);
R=20cm the radius of the spherical device;
I=1A the current of a hypothetical centered wire;
z vertical coordinate (normalized);
$$$\vec{e}_{\phi}$$$ the azimuthal unit vector;
N=180 (the higher the more the field resembles a single current)
A simulation with a static background field of 3T showed no change of simulation results and all expected effects were adding up.
Discussion
Negative µ-materials represent new pathways of focusing magnetic fields in the distance and are of extraordinary interest for medical purposes. Only a handful experimental validations exist, and some showed that magnetic fields can be manipulated inside inaccessibly volumes. The proposed variant of the magnetic replicator ensures spherical symmetry and allows for positioning of the patient head inside the replicator contrary to the original case where the replicator would need to be positioned tangential to the head and orthogonal to the scanner’s z-axis. The parameters I, d and N drastically influence the simulation outcome and various shapes of fields can be created and the ratio (d/R) and N restrict the current maximum. The field divergencies unfortunately limit practical purposes of magnetic replicators and would need to be taken into account. Unexplored is still the dependence of the $$$B_z$$$ field on spatially linear and time-varying gradients.Conclusion
Magnetic replicators for B0 shimming as well as for transcranial magnetic stimulation may overcome traditional methods especially concerning the locality of field manipulation, real-time field manipulation by current tuning and patient safety due to distant surface currents.Acknowledgements
We want to thank the Austrian Science Fund (FWF): Project Number TAI-676 (1000 Ideas Program)References
1.) Milton Graeme W, Nicorovici Nicolae-Alexandru P, McPhedran Ross C and Podolskiy Viktor A 2005A proof of superlensing in the quasistatic regime, and limitations of superlenses in this regime due to anomalous localized resonance Proc. R. Soc. A.4613999–4034http://doi.org/10.1098/rspa.2005.1570
2.) Navau C, Prat-Camps J, Sanchez A. Magnetic energy harvesting and concentration at a distance by transformation optics. Phys Rev Lett. 2012;109(26):263903. doi:10.1103/PhysRevLett.109.263903
3.) Navau, C., Mach-Batlle, R., Parra, A. et al. Enhancing the sensitivity of magnetic sensors by 3D metamaterial shells. Sci Rep 7, 44762 (2017). https://doi.org/10.1038/srep44762
4.) Mach-Batlle R, Bason MG, Del-Valle N, Prat-Camps J. Tailoring Magnetic Fields in Inaccessible Regions. Phys Rev Lett. 2020;125(17):177204. doi:10.1103/PhysRevLett.125.177204
5.) Mach-Batlle, Rosa, Albert Parra, Jordi Prat-Camps, Sergi Laut, Carles Navau, and Alvaro Sanchez. "Negative permeability in magnetostatics and its experimental demonstration." Physical Review B 96, no. 9 (2017): 094422.
6.) A. J. Ward & J. B. Pendry (1996) Refraction and geometry in Maxwell's equations, Journal of Modern Optics, 43:4, 773-793, DOI: 10.1080/09500349608232782
7.) Pendry JB, Schurig D, Smith DR. Controlling electromagnetic fields. Science. 2006;312(5781):1780-1782. doi:10.1126/science.1125907
Figures

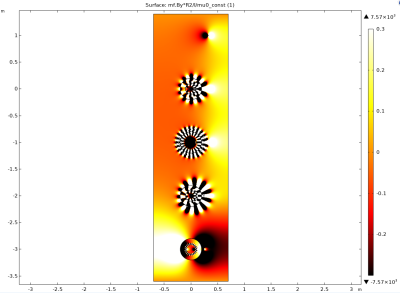
Figure 3: Top to bottom:
A single current and µ=1 wire;
a theoretical µ=-1 shell (without surface currents) with an right-centered inner current creates an inside-to-outside field similar as above;
using the currents derived in4 a µ=-1 shell can be mimicked (surface currents on a µ=1 shell);
a theoretical µ=-1 material with an outer current on the right which replicates the field to the inner shell (outside-to-inside);
a µ=1 material with surface currents replicating the field from outer-right to inner-right & inner-left to outer-left. Also replicas to the inner shell domain exist here