5195
Joint Distribution Modeling for Accelerated T1rho Reconstruction
Congcong Liu1, Zhuo-Xu Cui1, Yuanyuan Liu1, Chentao Cao1, Jing Cheng1, Yanjie Zhu1, Haifeng Wang1, and Dong Liang1,2
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Pazhou Lab, Guangzhou, China
1Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, 2Pazhou Lab, Guangzhou, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
Traditional hand-craft designed methods to accelerated T1rho mapping have limited characterisation capabilities, while deep learning methods lack the interpretability. On the other hand, the joint distribution is the most direct and accurate way to characterize the correlation between different images. Therefore, we attempt to propose a joint distribution estimation method and use it to construct a T1$$$\rho$$$ reconstruction model. In particular, we use a score-based diffusion model to model the joint distribution of acquired T1rho-weighted images. Moreover, the corresponding reconstruction model is solved using the Langevin gradient descent method. Finally, numerical experiments validate the effectiveness of the proposed method.Introduction
To quantify T1rho map, multiple T1rho-weighted images are acquired with various time-of-spin-lock times (TSL), which greatly extends the scan time [1], [2]. Traditional methods portray structural similarities between images by manually designing regularization, while ignoring information such as contrast [3]. Deep learning (DL) methods, on the other hand, learn correlations between images implicitly through neural network modules. However, networks that work on a black-box principle are complex in structure and lack the necessary interpretability [4]. From a probabilistic point of view, therefore, joint distribution modelling can accurately describe the similarity between images [5]. The emerging scored-based diffusion model for generative modeling based on estimating and sampling from the score of the logarithmic data density has demonstrated robust modeling properties for data distributions [6,7,8,9,10].In this work, we prospectively model the joint distribution between T1rho data to accelerate the raw data acquisition process, and proposed a novel T1rho acceleration approach based on scored-based diffusion model to characteristics the joint distribution of the relaxation datapoint. Preliminary experimental results have shown that the joint distribution modeling method proposed using T1rho as an example can arrive at strong feasibility.
Method
Considering maximum likelihood estimation, the reconstruction of MR image can be formulated as $$$p(x|y)$$$. The maximum likelihood estimation could provide the reconstruction image $$$x$$$. In this way, the reconstruction problem is recast as posterior probability calculations. In the case of joint distribution, such as images acquired by multiple TSL times, the maximum likelihood estimation will reformulate as follows,$$\mathop{\max} p(x_1,\cdots, x_n | y_1, \cdots, y_n) \qquad (1) $$
where $$$n$$$ denotes the number of joint distribution variables. This work collected T1rho-weighted maps of four different TSL times to fit the T1rho map (i.e., n = 4). Using the Bayesian formulation take the logarithm of both sides at the same time, (1) is reconstructed as follows
$$\begin{split} \mathop{\max} \log p(x_1,\cdots, x_n | y_1, \cdots, y_n) = \log p(x_1,\cdots, x_n) \\ + \log p(y_1,\cdots, y_n | x_1, \cdots, x_n) \end{split} \qquad (2) $$
Since the conditional probability of $$$y$$$ obeys the Gaussian distribution given $$$x$$$. In here, the probability density of formulating $$$y$$$ given $$$x$$$ is
$$ p(y_1, \cdots, y_n) \sim \prod_{i=1}^{n} e^{- \frac{||Ax_{i}-y_{i}||^2}{\sigma_{i}^2}} \qquad (3) $$
In this work, the maximum likelihood estimation task described in (2) is rewritten as $$$L(x_{1}, \cdots, x_{n})$$$. The gradient ascent algorithm is utilized to perform the maximum likelihood estimation of (2). That is,
$$X_{k+1} = X_{k} + \eta_{k}\nabla L(X_{k}) + \zeta_{k} \qquad (4) $$
where $$$x_{1}$$$ to $$$x_{4}$$$ are simply referred to as $$$X$$$. In here, $$$\nabla L(X_{k})$$$ is calculated as follows
$$\nabla L(X_{k}) = \nabla_{X}\log p(x_1,\cdots,x_{n}) + \left[\begin{array}{c}-\frac{A_{1}^{*}(A_{1}x_{1}-y_{1})}{\sigma_{1}^{2}} \\ \vdots\\ -\frac{A_{n}^{*}(A_{n}x_{n}-y_{n})}{\sigma_{n}^{2}} \end{array}\right] \qquad (5) $$
where $$$A^{*}$$$ is hermitian matrices of $$$A$$$. The joint distribution estimitation of $$$x_{1}$$$ to $$$x_{n}$$$ is un-tractable. Score-based diffusion model can estimate the $$$score$$$ of $$$p$$$, defined as $$$\nabla_{x}$$$log$$$p(x)$$$, by training a CNN denoising score matching [6]. Therefore, the gradient of the distribution of the original data can be approximated by training a neural network, and subsequent iterative solving tasks are sampled by annealed Langevin dynamics. Formally, we optimize the parameters $$$\theta$$$ of the score network with the following cost:
$$ \mathop{\min}_{\theta}\mathbb{E}_{x(0)}\mathbb{E}_{X(t)|X(0)}[||s_{\theta}(x_{1}(t), \cdots, x_{n}(t)) - \nabla_{X}p_{0t}(x_{1}(t),\cdots,x_{n}(t)|x_{1}(0),\cdots,x_{n}(0))||_{2}^{2}] \qquad (6) $$
Intuitively, one can also treat (6) as training the neural network to denoise the joint data point (i.e., various T1rho-weighted image). The network architecture stems from U-Net as suggested in [7]. Bring the trained denoising score matching network into (5), we have
$$ \nabla L(X_{k}) \approx s_{\theta}(x_{1}^{k},\cdots,x_{n}^{k}) + \left[\begin{array}{c}-\frac{A_{1}^{*}(A_{1}x_{1}-y_{1})}{\sigma_{1}^{2}} \\ \vdots\\ -\frac{A_{n}^{*}(A_{n}x_{n}-y_{n})}{\sigma_{n}^{2}} \end{array}\right] \qquad (7)$$
The gradients in (6) can be computed once the training is complete, and the T1rho-accelerated reconstruction can be performed by substituting the gradients into the sampling reconstruction task in (4). Specifically, in the current joint distribution modeling in T1rho, $$$x_{1}$$$ to $$$x_{n}$$$ correspond to the weighted images corresponding to the four TSL moments (TSL = 1, 25, 45, and 64 $$$ms$$$) collected in this work, respectively.
The IRB (institutional review board) approved in vivo human brain experiments that were performed on a 3T uMR790 scanner (United Imaging, Shanghai, China). The full-sampled in vivo data (14 healthy volunteers) were recruited for T1rho scanning and then performed retrospective sub-sampling. The scan parameters are: 32-ch coil, FOV = $$$240\times200\times30$$$, voxel size: $$$1\times1\times3 \ mm$$$, TR/TE=5.55 / 2.00 $$$ms$$$, ETL length: 50, TSL: 1, 25, 45, 65 $$$ms$$$, spin-lock frequency = 500 $$$Hz$$$. Variable density and random retrospective sub-sampling patterns along phase encoding direction provide 8x time reduction (16 auto-calibration signals (ACS)). Coil sensitivity maps (CSM) were estimated using the ESPIRiT method described earlier [11].
Results
A schematic diagram of the bidirectional process is given in Fig. 1. The weighted images corresponding to different TSL are perturbed with Gaussian noise of differentintensities. The results in Fig.2 show that the uniform pattern has a certaintranscendence relative to the random pattern in terms of artifact-free. From T1rho maps by exploiting curve fitting, the proposed method is capable of quantification of T1rho relaxation times in uniform pattern with 8-fold acceleration.Conclusion
In summary, this work based on a score-based diffusion model proposes a method for estimating the joint distribution of T1rho data to describe the correlation between different images accurately.Acknowledgements
Congcong Liu and Zhuo-Xu Cui contributed equally to this work. This work was partially supported by the National Natural Science Foundation of China (61871373, 62271474, 81830056, U1805261, 81729003, 81901736, 12026603, 12026603 and 81971611), the Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000 and XDC07040000), the High-level Talent Program in Pearl River Talent Plan of Guangdong Province (2019QN01Y986), the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province (2020B1212060051), the Science and Technology Plan Program of Guangzhou (202007030002), the Key Field R&D Program of Guangdong Province (2018B030335001), the Shenzhen Science and Technology Program, Grant Award (JCYJ20210324115810030), and the Shenzhen Science and Technology Program (Grant No. KQTD20180413181834876, and KCXF20211020163408012).References
- Zhu, Yanjie, et al. "A 4‐minute solution for submillimeter whole‐brain T1ρ quantification." Magnetic Resonance in Medicine 85.6 (2021): 3299-3307.
- Liu, Yuanyuan, et al. "Accelerating the 3D T1ρ mapping of cartilage using a signal-compensated robust tensor principal component analysis model." Quantitative Imaging in Medicine and Surgery 11.8 (2021): 3376.
- Zibetti, Marcelo VW, et al. "Compressed sensing acceleration of biexponential 3D‐T1rho relaxation mapping of knee cartilage." Magnetic resonance in medicine 81.2 (2019): 863-880.
- Li, Hongyu, et al. "Ultra-fast simultaneous T1rho and T2 mapping using deep learning." ISMRM Annual Meeting. 2020.
- Jiang, Jue, et al. "PSIGAN: joint probabilistic segmentation and image distribution matching for unpaired cross-modality adaptation-based MRI segmentation." IEEE transactions on medical imaging 39.12 (2020): 4071-4084.
- Cui, Zhuo-Xu, et al. "Self-Score: Self-Supervised Learning on Score-Based Models for MRI Reconstruction." arXiv preprint arXiv:2209.00835 (2022).Cao, Chentao, et al. "High-Frequency Space Diffusion Models for Accelerated MRI." arXiv preprint arXiv:2208.05481 (2022).
- Song, Yang, and Stefano Ermon. "Generative modeling by estimating gradients of the data distribution." Advances in Neural Information Processing Systems 32 (2019).
- Song, Yang, et al. "Score-based generative modeling through stochastic differential equations." arXiv preprint arXiv:2011.13456 (2020).
- Jalal, Ajil, et al. "Robust compressed sensing mri with deep generative priors." Advances in Neural Information Processing Systems 34 (2021): 14938-14954.
- Luo, Guanxiong, et al. "MRI reconstruction using deep Bayesian estimation." Magnetic resonance in medicine 84.4 (2020): 2246-2261.
- Qiu, Zhilang, et al. "Highly accelerated parallel MRI using wave encoding and virtual conjugate coils." Magnetic resonance in medicine 86.3 (2021): 1345-1359.
Figures
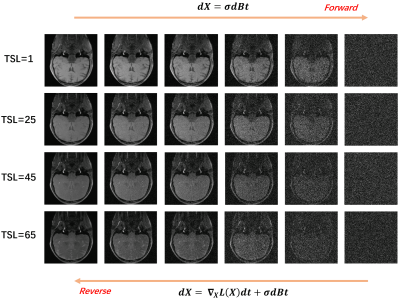
Fig.1 Overall block diagram including Gaussian kernel perturbation and sample generation. Transforming T1rho data to a simple noise distribution can be accomplished at various times. The gradient of the learning joint data distribution given in the figure goes in the forward perturbation process applied in the reverse Langevin dynamic sampling.
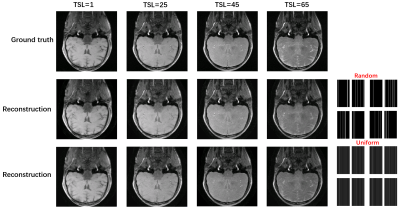
Fig. 2 Sampling generation results of TSL-weighted images with different sampling patterns (variable density and uniform with 18 ACS) at 8x acceleration factor. The sampling pattern for each group of T1rho-weighted plots is given at the bottom right.
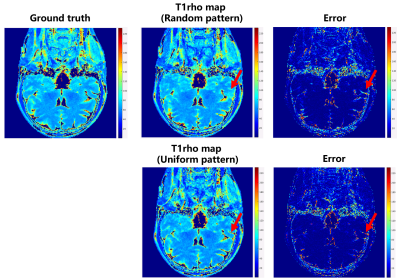
Fig. 3 The T1rho map of the proposed method under different acceleration patterns using curve fitting to assess the feasibility of the proposed method. One can see that the T1rho map can be obtained under both sampling templates closer to the ground truth. The proposed method under uniformly sampled templates is superior for T1rho quantification relative to random templates. The red arrows point out the superiority of the detail section in the uniform pattern.
DOI: https://doi.org/10.58530/2023/5195