Synopsis

Keywords: Machine Learning/Artificial Intelligence, Quantitative Imaging, Intravoxel incoherent motion

Recently, various methods have been proposed to quantify intravoxel incoherent motion parameters. Many studies have shown that quantification methods using deep learning can accurately estimate IVIM parameters. Unsupervised learning is useful when quantifying IVIM parameters for in-vivo data because it does not require label data. However, in some cases, loss function does not converge as iteration increases. Constraint functions can be used to solve these problems by limiting the range of estimated outputs. In this study, we investigated the effects of constraint function to limit the range of estimated output.

Introduction

The concept of IVIM was introduced to describe diffusion and perfusion in tissue using biexponential model by Le Bihan (1,2). Although various methods for quantification of IVIM have been proposed, it is still challenging to quantify IVIM parameters accurately (3). Recently, deep learning methods have been studied to accurately quantify IVIM parameters (4,5). Unsupervised learning is useful when quantifying IVIM parameters of in-vivo data because it does not require label data. However, in some cases, loss function diverges as iteration increases. Constraint function can be used to solve these problems by limiting the range of estimated output. In this study, we investigate the effects of constraint function and scaling when quantifying IVIM parameters using unsupervised learning.

Methods

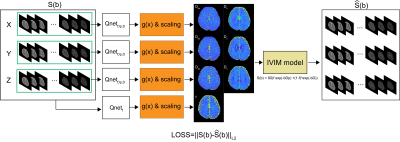
Using unsupervised learning technique, a deep neural network estimates the IVIM parameters from the diffusion weighted images. The deep neural network is trained by minimizing a loss function between the measured diffusion weighted MR signals and the synthesized diffusion weighted MR signals from the estimated IVIM parameters. IVIM model is delineated as follows.
$$S(b)=S_0( f \cdot exp(-bD_p)+(1-f)\cdot exp(-bD))$$
where $$$S(b)$$$ is the diffusion-weighted MRI signal for a b-value of $$$b$$$, $$$S(b)$$$ is the MRI signal when the b-value is zero,$$$f$$$ is the perfusion fraction, $$$D_p$$$ is the perfusion coefficient, and $$$D$$$ is the diffusion coefficient.
Various approaches have been proposed to quantify IVIM parameters by using unsupervised learning methods (4,6). In this study, IVIM parameters were quantified by Qnet, which estimated direction-dependent parameters in each orthogonal direction (6). The perfusion coefficient and diffusion coefficient, which are direction-dependent parameters, are estimated from the DWIs in the corresponding direction.
As shown in Figure 1, there are two Qnets for quantification of IVIM parameters, direction independent Qnet (Qnet_f) for perfusion fraction and direction dependent Qnet (Qnet_{Dp, D}) for perfusion coefficient and diffusion coefficient. The direction independent Qnet estimates perfusion fraction using all diffusion weighted images of three orthogonal diffusion gradients. The direction dependent Qnet estimates perfusion coefficient and diffusion coefficient using the diffusion weighted images of the corresponding directions. The Qnet consists of three convolutional layers with one by one kernel size. Each convolution layer has 30 kernels.
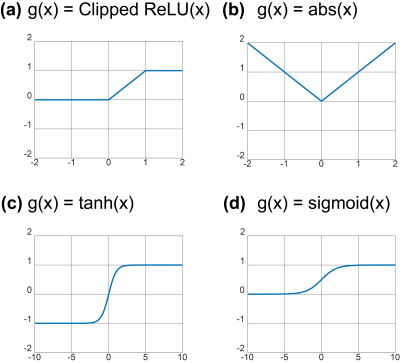
The output of Qnet is constrained by various constraint function $$$g(x)$$$. To constrain the output of Qnet, we used clipped ReLU, absolute, hyperbolic tangent, sigmoid function as $$$g(x)$$$. The constrained output of $$$g(x)$$$ is scaled to the IVIM parameter ranges. We also compared the results with and without constraints and scaling. In this study, the output of g(x) is scaled to the IVIM parameter ranges of $$$f\in[0,0.5], D\in[0,3\times10^{-3}]mm^2 /s,D_p\in [5\times10^{-3},100\times 10^{-3}]mm^2/s$$$.

Digital phantom simulations

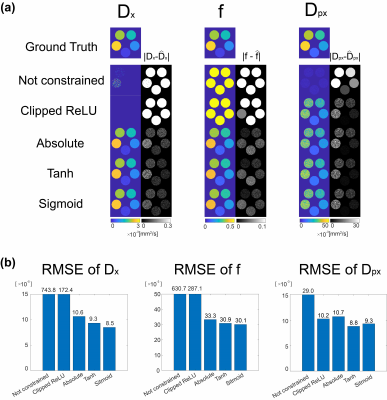
In order to analyze the accuracy of quantification, we performed digital phantom simulations. As shown in Figure 3, we simulated a digital phantom with five different values of one parameter and the other randomly distributed digital phantoms in the ranges of $$$f\in[0.05,0.45], D\in[0.3\times10^{-3},2.7\times10^{-3}]mm^2 /s,D_p\in [10\times10^{-3},45\times 10^{-3}]mm^2/s $$$. In Figure 3, to be specific, in order to analyze the quantification performance for $$$D_x$$$, diffusion weighted MR signals are synthesized based on the five different values for $$$D_x$$$ and randomly distributed $$$f, D_y, D_z, Dp_x, Dp_y,$$$ and $$$Dp_z$$$. Then, Qnet estimated IVIM parameters with various constraint functions. Results were analyzed in the same way for $$$f$$$ and $$$D_px$$$.

In-vivo experiment

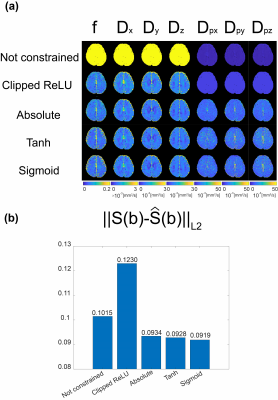
Brain MRI experiments were performed on a 3 Tesla MRI scanner. In vivo experiments were conducted with approval of the institutional review board. A spin-echo EPI sequence was used for the experiments with the imaging parameters as TR = 6000ms; TE = 83ms; number of averages = 1; FOV = 240mm$$$\times$$$240mm; matrix size = 120$$$\times$$$120; slice thickness = 2mm; and bandwidth = 1544Hz/pixel. The diffusion weighted images were acquired for b-values of 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 400, 700, and 1000 $$$[s/mm^2]$$$ with three orthogonal diffusion gradient directions. IVIM parameters were estimated by Qnet from the obtained diffusion weighted images. In order to analyze the performance of IVIM quantification for in-vivo data, we calculated $$$L2$$$ norm between the obtained diffusion weighted signals, $$$S(b)$$$, and the synthesized MR signals from the estimated IVIM parameters, $$$\hat{S}(b)$$$ .

Results

As shown in Figure 3, when output of Qnet was not constrained, quantification performance was very low. Furthermore, clipped ReLU function tended to saturate the output. The clipped ReLU is not suitable for finding accurate parameters. For in-vivo data, the results were different according to the constraint function. Similar to the results of digital phantom simulation, quantification was not accurate when the output of Qnet was not constrained and the clipped ReLU was used as the constraint function. On the other hand, IVIM parameters were well estimated when absolute, hyperbolic tangent, and sigmoid functions were used for constraint function. However, the prefusion fraction was estimated slightly lower when absolute was used than when hyperbolic tangent and sigmoid were used.

Discussion & Conclusion

The phantom simulation and in-vivo results showed that the quantification using unsupervised learning had high performance only when the output was constrained and scaled. Absolute function performed somewhat poorly compared to Sigmoid and Tanh. The importance of the constraint function was shown in this study. It should be used carefully when quantifying IVIM parameters using unsupervised learning.

Acknowledgements

This research was supported by a grant from the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health and Welfare, Republic of Korea (grant number: HI14C1135). This work was also supported by the Korea Medical Device Development Fund grant funded by the Korea government (the Ministry of Science and ICT; the Ministry of Trade, Industry and Energy; the Ministry of Health and Welfare; the Ministry of Food and Drug Safety) (project number: 1711138003, KMDF-RnD KMDF_PR_20200901_0041-2021-02 ).