Synopsis

Keywords: Machine Learning/Artificial Intelligence, Quantitative Imaging

In quantitative MRI, tissue properties are estimated from MRI data using bio-physical models that relate the MRI signal to the underlying tissue properties via model parameters. Deep learning can improve parameter estimation, but is conventionally dependent on the input being either a fixed set of input signals or a series of regularly sampled signals. Neural controlled differential equations (NCDEs) are models that are independent of the configuration of input data. NCDEs have similar performance to state-of-the-art acquisition-specific deep learning methods in estimating intra-voxel incoherent motion parameters. Therefore, NCDEs are a generic purpose tool for parameter estimation in quantitative MRI.

Introduction

In quantitative MRI, tissue properties are estimated from MRI data using bio-physical models that relate the MRI signal to the underlying tissue properties via model parameters. Conventionally, such parameter estimation is done using voxelwise least squares fitting to images with different contrast weightings. However, least squares fitting is strongly affected by noise. Deep learning for estimating quantitative MRI parameter maps has great potential to be more noise robust and thus more accurate in clinical practice¹.

To learn the transformation of a series of signals to quantitative MRI parameters, current deep learning algorithms rely on the input being either a fixed set of signals^2,3 or a sequence of regularly sampled signals⁴, limiting their practical use. In quantitative MRI, the configuration of signals is often variable between studies, prohibiting conventional neural networks from deriving a generically applicable approximation of the underlying process responsible for generating the measured signals. Neural Ordinary Differential equations are a family of machine learning methods approximating system dynamics in continuous time by learning the underlying differential equation using a neural network⁵. Neural Controlled Differential Equations (NCDEs) incorporate incoming data, which can be irregularly sampled and partially observed, to control the learnt differential equation with observations and thereby creating an explicit dependence of the output on the learnt system dynamics and the input series⁶. This allows NCDEs to be a generic tool for quantitative MRI parameter estimation, independent of acquisition protocol.

We implemented NCDEs and demonstrate their applicability for quantitative MRI parameter estimation on both simulated and in-vivo data for intra-voxel incoherent motion (IVIM) MRI.

Methods

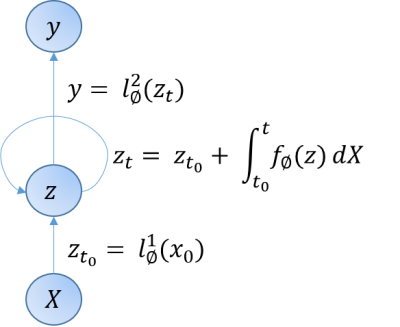
1. Model
An NCDE-based architecture was implemented, trained and evaluated using PyTorch (version 1.10.1) and torchcde (version 0.2.5)⁶. The NCDE is schematically visualized in figure 1.
IVIM allows us to assess tissue diffusion and perfusion properties by measuring signal decay as a function of diffusion weighting, expressed in b-values, expressed as:
$$S(b)=S0((1-f)e^{-bD}+fe^{-bD^*}) \hspace{10pt} (1)$$
Here, $$$D$$$ is the diffusion coefficient, $$$D^*$$$ the pseudo-diffusion coefficient, $$$f$$$ the perfusion fraction and $$$S0$$$ the signal intensity without diffusion weighting.
We used an NCDE to map $$$S(b)$$$ to an output vector $$$y$$$, see figure 1. $$$y$$$ contains the coefficients to compute model parameters, i.e. for $$$D$$$:
$$D=D_{min}+sigmoid(y[1])(D_{max}-D_{min}) \hspace{10pt} (2)$$
Based on the predicted model parameters together with the set of b-values, a signal decay curve $$$S_{pred}(b)$$$ is predicted according to (1).
The model is trained by minimizing a physics-informed loss², comparing the measured signal intensities to the predicted signal intensities at B, the set of measured b-values, following:
$$L=\frac{1}{len(B)}\sum_{b\epsilon B}(S_{measured}(b)-S_{pred}(b))^2 \hspace{10pt} (3)$$

2. Simulations
100,000 signal decay curves were simulated based on the IVIM model as in (1) from uniformly sampled combinations of $$$D$$$ (0.0003–0.0035 $$$\frac{mm^2}{s}$$$), $$$D^*$$$ (0.05–0.2 $$$\frac{mm^2}{s}$$$) and $$$f$$$ (0–0.6). Rician noise with a signal-to-noise ratio (SNR) sampled from a uniform distribution between 50 and 100 was added to the signal decay curves. The signal decay curves were used to train the NCDE model using the loss in (3). The NCDE model was trained with signal decay curves generated with variable b-values.
Similarly, 10,000 signal decay curves per SNR level were generated for evaluation of the NCDE model, IVIMNET (a state-of-the-art neural network for estimating IVIM model parameters based on fixed b-values³) and least squares fitting. Performance was measured using parameter-specific normalized root mean square error (nRMSE) as a function of SNR.

3. In-vivo data
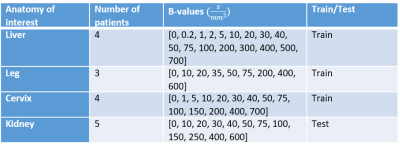
The in-vivo data from four different studies that were used for training of the NCDE model and evaluation of the NCDE model and least squares fitting are described in table 1. In five patients, the NCDE model was visually compared to the least squares estimation.

Results

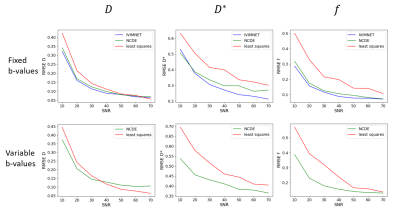
1. Simulations
On a set of fixed b-values , the NCDE model was able to infer IVIM parameters from signal decay curves with similar accuracy as IVIMNET, and improved accuracy compared to least squares over all SNR levels, see figure 2. Evaluated on a randomly sampled set b-values of variable length, the NCDE model also showed improved performance compared to least squares fitting, especially on data with low SNR levels.

2. In-vivo data
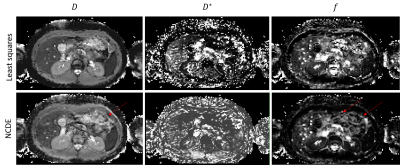
The NCDE model reconstructed more spatially homogeneous parameter maps than least squares estimation, appearing to be less affected by noise in the input data, see figure 3 for an example.

Discussion

We are the first to demonstrate the applicability of NCDEs as a generic tool for quantitative MRI parameter estimation by showing that NCDEs have comparable performance to acquisition-specific neural networks, without their shortcomings. NCDEs are applicable irrespective of acquisition protocol, on the condition that the dynamics of the input sequence are described by the approximated differential equation. Other quantitative MRI dynamics can be learned by adapting the loss function and using appropriate data.

In the high SNR data range, least squares is a good estimator for model parameters, but in the lower SNR data range typically seen in DWI data, neural networks appear to learn a more robust estimation.

Conclusion

NCDEs can be used as a generic tool for quantitative MRI parameter estimation. In IVIM parameter estimation, NCDEs outperform least squares fitting and perform similarly to acquisition-specific neural networks.

Acknowledgements

The KWF Dutch Cancer Society supported this work under Grant No. KWF-UVA 2021.13785