5183
Deep Learning Quantification of Magnetic Resonance Spectroscopy Based on Basis set and Exponential Priors1Department of Electronic Science, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, 2McLean Hospital, Harvard Medical School, Belmont, MA, United States, 3Philips Healthcare, Beijing, China, 4School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China, 5Department of Radiology, The Zhongshan Hospital affiliated to Xiamen University, Xiamen, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Brain, Magnetic Resonance Spectroscopy, Quantification
Quantification of 1H-MRS is difficult because of the overlapping of individual metabolite signals, non-ideal acquisition conditions, and strong background signal interference. We introduced Deep Learning (DL) method to learn these effects to improve the accuracy of the quantification. Results indicate that, compared with the conventional method LCModel, the proposed Qnet (Quantification deep learning network) shows better quantification for both simulated and in vivo acquired MRS data with lower fitting errors and enhanced stability.Purpose
Proton Magnetic Resonance Spectroscopy (1H-MRS) is an important tool for non-invasive in vivo metabolic detection but its quantification can be difficult. This difficulty lies in three aspects1: overlapping of individual metabolite signals, signal distortion due to non-ideal acquisition conditions, and strong background signal (baseline) interference. The popular quantification software, LCModel2, considers those effects in quantification by designing several empirical prior models and regularization terms. However, the process of solving such a large quantitative model is very complicated. Especially when the signal-to-noise ratio (SNR) of the input MRS signal is low, the solutions may have a large deviation3. Therefore, we introduced Deep Learning (DL)4-13 with the powerful nonlinear fitting capability to reduce the complexity and improve the accuracy of the overall quantitative solution.Method
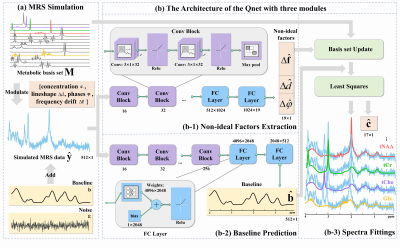
Data preparation: All in vivo data acquisition was conducted on the Philips 3T DNA scanner with a 32-channel head coil, using a point-resolved spectroscopy (PRESS) sequence, and the fast spin-echo sequence was used to acquire T1-weighted images of the brain for voxel selection. The following MRS experimental parameters: TR/TE= 2000 ms / 35 ms, voxel size= 20 mm × 20 mm × 20 mm, number of data points= 2048, spectral bandwidth= 2000 Hz, Number of Signal Averages (NSA)= 128, and water suppress processing was performed by excitation. A total of 20 MRS data were collected from 14 healthy subjects (The regions collected included white matter tissue from the anterior and posterior frontal lobes (16), parietal lobes (1), occipital lobes (1) and anterior and posterior cingulate gyrus (2)). The human experiment was approved by the Medical Ethics Committee of the Zhongshan Hospital affiliated to Xiamen University. The simulated data is based on the measured experimental parameters and its concentration range of metabolites, non-ideal factors, and baseline are referred from previous study10 and our measured data.Model Design: We separated two of the complex parts in the quantification, non-ideal conditional factors (modelled by exponential functions) extraction, and baseline (modelled by Gaussian functions) prediction, to DL. Specifically, the baseline and non-ideal factors are extracted directly by DL, and then the metabolic basis set simulated by quantum mechanical and exponential models14,15 would be updated by them. Finally, the remaining part only just solves ordinary linear least squares between the input and the updated basis set. The entire framework described above (shown in Figure 1) is called Qnet (Quantification deep learning network).
Results
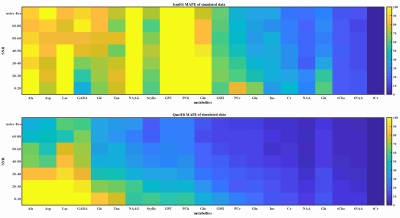
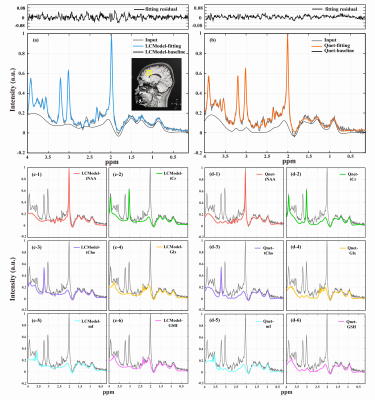
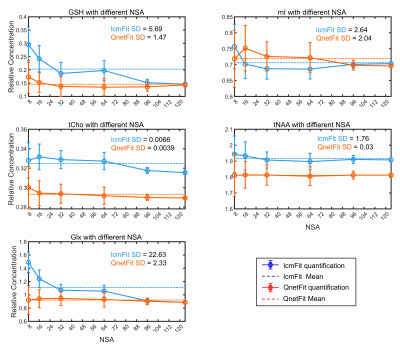
Qnet was tested on both 700 simulated data and 20 in vivo healthy subjects’ bran MRS data, and the results were compared with LCModel. Figure 2 shows the quantification Mean Absolute Percentage Error (MAPE) of Qnet and LCModel on simulated data with different SNR. Qnet not only shows lower fitting errors for quantification of low-concentration metabolites that are difficult to be detected at 3T (such as Ala, Asp, GABA, etc) but also has advantages in the quantification of some dominant metabolite signals (tNAA, tCho, and Glx).For the no-label in vivo test, spectral fittings for different metabolites by LCModel and Qnet showed no significant difference on the 128 NSA MRS data, but the fitting residuals by Qnet were reduced compared with those by LCModel (Figure 3). Figure 4 shows the metabolite quantification by LCModel and Qnet in one in vivo MRS data under different NSA. As can be seen, the standard deviations (SDs) of Qnet for the quantification of five dominant metabolites are smaller than those of LCModel, implying that the stability of Qnet is better than that of LCModel in the face of spectra with different SNR.
Conclusion
DL is possible to extract non-ideal factors and baselines from poor inputs because of its supervised learning. there are corresponding labels to guide learning, despite the low SNR o of the input. Therefore, DL is possible to extract non-ideal factors and baselines from poor inputs. Based on this, we generated amounts of simulated MRS data to train the proposed Qnet which is based on the basis set and exponential Priors. Results show that, compared with the LCModel, the quantification error of the proposed Qnet is lower (less than 10%) in the simulated data test, and presented more stable quantification results in the in vivo MRS data with different NSA (indicates different SNR).Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (62122064, 61971361, 61871341, 61811530021), Natural Science Foundation of Fujian Province of China (2021J011184), Health-Education Joint Research Project of Fujian Province (2019-WJ-31), Xiamen University Nanqiang Outstanding Talents Program.
The correspondence should be sent to Prof. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
[1] R. A. De Graaf, In vivo NMR spectroscopy: principles and techniques (book), John Wiley & Sons, 2019.
[2] S. W. Provencher, “Automatic quantitation of localized in vivo 1H spectra with LCModel,” NMR in Biomedicine: An International Journal Devoted to the Development and Application of Magnetic Resonance In Vivo, vol. 14, no. 4, pp. 260-264, 2001.
[3] M. Marjańska, D. K. Deelchand, R. Kreis, and t. I. M. S. G. F. C. Team, “Results and interpretation of a fitting challenge for MR spectroscopy set up by the MRS study group of ISMRM,” Magnetic Resonance in Medicine, vol. 87, no. 1, pp. 11-32, 2022.
[4] D. Chen, Z. Wang, D. Guo, V. Orekhov, and X. Qu, “Review and prospect: deep learning in nuclear magnetic resonance spectroscopy,” Chemistry–A European Journal, vol. 26, no. 46, pp. 10391-10401, 2020.
[5] T. Qiu, Z. Wang, H. Liu, D. Guo, and X. Qu, “Review and prospect: NMR spectroscopy denoising & reconstruction with low-rank hankel matrices and tensors,” Magnetic Resonance in Chemistry., vol. 59, no. 3, pp. 324-345, 2021.
[6] Y. Li, Z. Wang, R. Sun, and F. Lam, “Separation of metabolites and macromolecules for short-TE 1 H-MRSI using learned component-specific representations,” IEEE Transactions on Medical Imaging, vol. 40, no. 4, pp. 1157-1167, 2021.
[7] Y. Huang, J. Zhao, Z. Wang, V. Orekhov, D. Guo, and X. Qu, “Exponential signal reconstruction with deep hankel matrix factorization,” IEEE Transactions on Neural Networks and Learning Systems, 2021, DOI: 10.1109/TNNLS.2021.3134717.
[8] Z. Wang, D. Guo, Z. Tu, Y. Huang, Y. Zhou, J. Wang, L. Feng, D. Lin, Y. You, and T. Agback, “A sparse model-inspired deep thresholding network for exponential signal reconstruction--application in fast biological spectroscopy,” IEEE Transactions on Neural Networks and Learning Systems, 2022, DOI: 10.1109/TNNLS.2022.3144580.
[9] X. Qu, Y. Huang, H. Lu, T. Qiu, D. Guo, V. Orekhov, and Z. Chen, “Accelerated nuclear magnetic resonance spectroscopy with deep learning,” Angewandte Chemie International Edition, vol. 59, no. 26, pp. 10297-10300, 2019.
[10] H. H. Lee, and H. Kim, “Intact metabolite spectrum mining by deep learning in proton magnetic resonance spectroscopy of the brain,” Magnetic resonance in medicine, vol. 82, no. 1, pp. 33-48, 2019.
[11] F. Lam, Y. Li, and X. Peng, “Constrained magnetic resonance spectroscopic imaging by learning nonlinear low-dimensional models,” IEEE transactions on medical imaging, vol. 39, no. 3, pp. 545-555, 2019.
[12] S. S. Gurbani, S. Sheriff, A. A. Maudsley, H. Shim, and L. A. Cooper, “Incorporation of a spectral model in a convolutional neural network for accelerated spectral fitting,” Magnetic resonance in medicine, vol. 81, no. 5, pp. 3346-3357, 2019.
[13] N. Hatami, M. Sdika, and H. Ratiney, “Magnetic resonance spectroscopy quantification using deep learning,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, 2018, pp. 467-475.
[14] R. Simpson, G. A. Devenyi, P. Jezzard, T. J. Hennessy, and J. Near, “Advanced processing and simulation of MRS data using the FID appliance (FID‐A)—an open source, MATLAB‐based toolkit,” Magnetic resonance in medicine, vol. 77, no. 1, pp. 23-33, 2017.
[15] Q. Yang, Z. Wang, K. Guo, C. Cai, and X. Qu, “Physics-driven Synthetic Data Learning for Biomedical Magnetic Resonance,” Signal Processing Magazine, 2022, DOI: 10.1109/MSP.2022.3183809.
Figures