5175

Integrating intravoxel incoherent motion and diffusion tensor MRI of the brain into a single fast acquisition - a model-selection study

Olaf Dietrich¹, Mengfei Cai², Anil Tuladhar², Mina Jacob², Gerald Drenthen³, Jacobus Jansen^3,4, José Marques², Jens Ricke¹, Frank-Erik de Leeuw², Marco Duering⁵, and Walter Backes³
¹Department of Radiology, LMU University of Munich, Munich, Germany, ²Department of Neurology, Donders Center for Medical Neurosciences, Radboud University Medical Center, Nijmegen, Netherlands, ³Schools for Mental Health and Neuroscience (MHeNs) and Cardiovascular Diseases (CARIM), Department of Radiology and Nuclear Medicine, Maastricht University Medical Center, Maastricht, Netherlands, ⁴Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands, ⁵Medical Image Analysis Center (MIAC AG) and qbig, Department of Biomedical Engineering, University of Basel, Basel, Switzerland

Synopsis

Keywords: Diffusion/other diffusion imaging techniques, Diffusion Tensor Imaging, Intravoxel incoherent motion MRI; Model selection; Brain; Cerebral small vessel disease

The acquisition of IVIM and DTI data of the brain can be integrated into a single measurement, which offers the possibility to determine orientation-dependent (tensorial) perfusion parameters in addition to established IVIM and DTI parameters. The purpose of this study was to evaluate the feasibility of such an integrated IVIM-DTI protocol with a clinically feasible scan time below 6 minutes and to establish the maximum number of DTI and IVIM tensor parameters that can reliably be determined with this approach by comparing 17 different IVIM-diffusion models with 4 to 19 model parameters.

Introduction

Diffusion-weighted MRI of the brain is a well-established imaging technique that is sensitive to incoherent motion of spins caused by their thermal energy and, in vivo, also to incoherent motion caused by pseudo-random flow^{1, 2}. Two particularly important variants of diffusion-weighted MRI in the brain are diffusion tensor imaging (DTI), which can quantify the mobility of water molecules along different spatial orientations^3-5, and intravoxel incoherent motion (IVIM) MRI, which is sensitive to capillary perfusion (“pseudo-diffusion”)^6-8. The acquisition of IVIM data and DTI data of the brain can be integrated into a single measurement, which, in particular, offers the possibility to determine orientation-dependent (tensorial) perfusion parameters in addition to established IVIM and DTI parameters. The purpose of this study was to evaluate the feasibility of such a protocol with a clinically feasible scan time below 6 minutes and to establish the maximum number of DTI and IVIM tensor parameters that can reliably be determined with this approach.

Methods

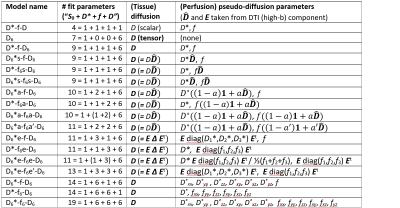
We acquired diffusion-weighted images of the brain at 3T in 20 elderly participants with cerebral small vessel disease using a multiband echoplanar imaging sequence with 15 b-values between 0 and 1000 s/mm² and 6 noncollinear diffusion gradient directions for each b-value. The acquisition time was 5:21 min. 17 different IVIM-diffusion models with 4 to 19 parameters were implemented, which modeled diffusion as well as perfusion fraction and pseudo-diffusion as scalar or tensor quantities (Table in Fig. 1). Models were derived from the most general 19-parameter model for the signal $$$S$$$ (depending on the diffusion weighting, $$$b$$$, and the diffusion-gradient orientation, $$$\mathbf{g}$$$):
$$S(b,\mathbf{g}) = S_0 \left( (1-\mathbf{g}^t \mathbf{f} \mathbf{g}) \exp (-b \,\mathbf{g}^t \mathbf{D} \mathbf{g}) + \mathbf{g}^t \mathbf{f} \mathbf{g} \exp (-b \,\mathbf{g}^t \mathbf{D^\ast} \mathbf{g}) \right) $$
with a symmetric 3×3 (tissue) diffusion tensor, $$$\mathbf{D}$$$, a symmetric 3×3 pseudo-diffusion (perfusion) tensor, $$$\mathbf{D^\ast}$$$, and a symmetric 3×3 f-tensor, $$$\mathbf{f}$$$, describing anisotropic perfusion signal fractions. To reduce the number of parameters in some of the models, $$$\mathbf{D^\ast}$$$ and/or $$$\mathbf{f}$$$ were selectively set to scalars or to tensors with fewer degrees of freedoms using tensorial properties (such as the anisotropy or the eigenvectors) of the tissue diffusion tensor $$$\mathbf{D}$$$ (cf. Table for details). When naming specific models, we denote the tissue diffusion tensor by “D₆”, the perfusion-fraction tensor by “f₆”, and the pseudo-diffusion tensor by “D₆^*” to differentiate from the scalar parameters “D”, “f”, and “D^*”. The notation “D₆^*s”/“f₆s” indicates tensors proportional to the tissue diffusion tensor $$$\mathbf{D}$$$, “D₆^*a”/“f₆a” tensors with reducible variable anisotropy derived from $$$\mathbf{D}$$$, and “D₆^*e”/“f₆e” tensors with the same eigenvectors as $$$\mathbf{D}$$$ (but independent eigenvalues).
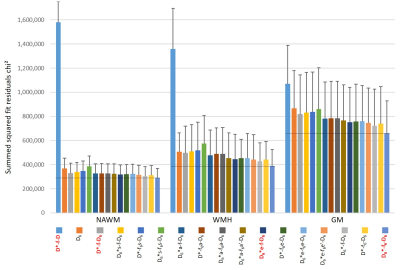
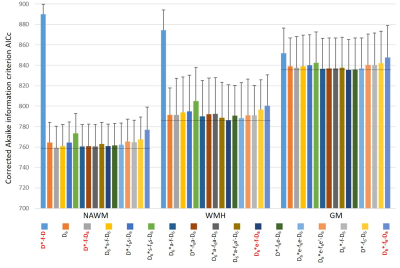
The models were compared in normal-appearing white matter (NAWM) and in WM with hyperintensities (WMH) as well as in gray matter (GM) with respect to their fitting performance based on the goodness of fit (sum of squared fit residuals, chi²) and the corrected Akaike information criterion (AICc)⁹.

Results and Discussion

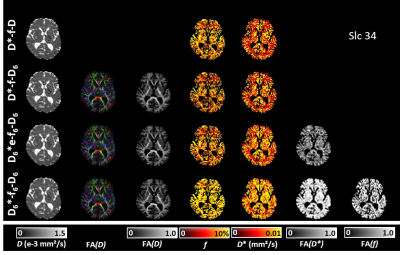
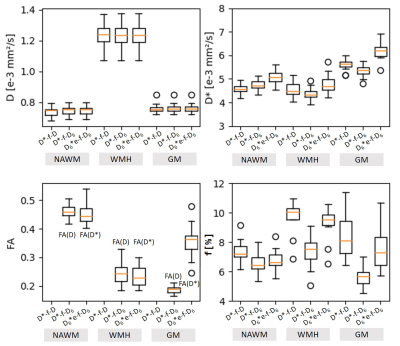
Lowest chi² values were found with the model D₆^*-f₆-D₆ (based on 3 independent 3×3 tensors) with the largest number (p=19) of model parameters (Fig.2). However, lowest AICc values (indicating the most adequate models for the acquired data) were obtained with a 9-parameter IVIM-DTI model (D^*-f-D₆, combining a 3×3 DTI tensor with isotropic perfusion/IVIM modeling) in NAWM, and with an 11-parameter model (D₆^*e-f-D₆, with a pseudo-diffusion tensor with the same eigenvectors as the diffusion tensor, but with different eigenvalues) in WMH and in GM (Fig.3). This latter model allowed for the additional calculation of the fractional anisotropy of the pseudo-diffusion tensor, which is not accessible with the usually performed IVIM acquisitions based on three orthogonal diffusion-gradient directions.
Our further analyses focused on the 9-parameter and 11-parameter IVIM-DTI models mentioned above as well as on the traditional tensor-free (scalar) 4-parameter IVIM model D^*-f-D and the 19-parameter model D₆^*-f₆-D₆. A visual comparison of the parameter maps determined with these four IVIM models is presented in Fig.4, showing consistent maps for the first 3 models, but biased IVIM maps (with systematically higher values) for the model D₆^*-f₆-D₆. The models D^*-f-D₆ (p = 9) and D₆^*e-f-D₆ (p = 11), favored by the Akaike criterion, were used to derive quantitative diffusion and perfusion (IVIM) parameters from all 20 participants and to compare these results to parameters from the traditional non-tensor IVIM analysis (D^*-f-D) with p = 4 free parameters. The results are summarized as boxplots in Fig.5 and show quantitative values in a similar range as earlier studies^10,^11,12. The fractional anisotropies of the diffusion tensor and of the pseudo-diffusion tensor were approximately 0.46 and 0.45 in NAWM, respectively, 0.24 and 0.23 in WMH, and 0.19 and 0.36 in GM.

Conclusions

Using a short (5:21 min) integrated IVIM-DTI protocol with 15 b-values and 6 diffusion directions for each b-value, we demonstrated that IVIM-DTI models with 9 and 11 parameters were most adequate to simultaneously determine parameters such as perfusion fraction, f, and pseudo-diffusion coefficient, D^*, as well as DTI parameters. The (11-parameter) model D₆^*e-f-D₆ with the lowest AICc values in WMH and GM allowed for the additional calculation of the fractional anisotropy of the pseudo-diffusion tensor, which is not accessible with the usually performed IVIM acquisitions based on three orthogonal diffusion-gradient directions.

Acknowledgements

No acknowledgement found.

References

1. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology. 1988; 168(2): 497-505. doi: 10.1148/radiology.168.2.3393671

2. Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986; 161(2): 401-407. doi: 10.1148/radiology.161.2.3763909

3. Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994; 103(3): 247-254. doi: 10.1006/jmrb.1994.1037

4. Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996; 201(3): 637-648. doi: 10.1148/radiology.201.3.8939209

5. Konieczny MJ, Dewenter A, Ter Telgte A, et al. Multi-shell Diffusion MRI Models for White Matter Characterization in Cerebral Small Vessel Disease. Neurology. 2021; 96(5): e698-e708. doi: 10.1212/WNL.0000000000011213

6. Federau C. Intravoxel incoherent motion MRI as a means to measure in vivo perfusion: A review of the evidence. NMR Biomed. 2017; 30(11). doi: 10.1002/nbm.3780

7. Schneider MJ, Dietrich O, Ingrisch M, et al. Intravoxel Incoherent Motion Magnetic Resonance Imaging in Partially Nephrectomized Kidneys. Invest Radiol. 2016; 51(5): 323-330. doi: 10.1097/RLI.0000000000000244

8. Schneider MJ, Gaass T, Ricke J, Dinkel J, Dietrich O. Assessment of intravoxel incoherent motion MRI with an artificial capillary network: analysis of biexponential and phase-distribution models. Magn Reson Med. 2019; 82(4): 1373-1384. doi: 10.1002/mrm.27816

9. Glatting G, Kletting P, Reske SN, Hohl K, Ring C. Choosing the optimal fit function: comparison of the Akaike information criterion and the F-test. Med Phys. 2007; 34(11): 4285-4292. doi: 10.1118/1.2794176

10. Hu YC, Yan LF, Han Y, et al. Can the low and high b-value distribution influence the pseudodiffusion parameter derived from IVIM DWI in normal brain? BMC Med Imaging. 2020; 20(1): 14. doi: 10.1186/s12880-020-0419-0

11. Wong SM, Backes WH, Zhang CE, et al. On the Reproducibility of Inversion Recovery Intravoxel Incoherent Motion Imaging in Cerebrovascular Disease. AJNR Am J Neuroradiol. 2018; 39(2): 226-231. doi: 10.3174/ajnr.A547

12. Vieni C, Ades-Aron B, Conti B, et al. Effect of intravoxel incoherent motion on diffusion parameters in normal brain. Neuroimage. 2020; 204: 116228. doi: 10.1016/j.neuroimage.2019.116228

Figures

Fig. 1 (Table): Overview over all 17 evaluated IVIM-DTI signal models. ($$$\mathbf{\hat D}$$$ (D with hat) is the normalized D tensor with trace 3. a is an anisotropy scaling factor combining the normalized (generally anisotropic) D tensor $$$\mathbf{\hat D}$$$ and the isotropic identity tensor. E is the orthogonal matrix with eigenvectors of D, Δ is the diagonal matrix with eigenvalues of D.)

Fig. 2: Summed squared fit residuals chi² (mean values and error bars indicating the standard deviations over individual median values of all 20 participants) of the 17 IVIM models in NAWM, WMH, and GM; best-fitting models have lowest chi² values within each tissue region (indicated by horizontal black line topping the D₆^*-f₆-D₆ model). Models used for further analysis below are indicated by red names.

Fig. 3: AICc model comparison (mean values and standard deviations over individual median values of all 20 participants) of the 17 IVIM models in three brain regions (NAWM, WMH, GM); preferred models have lowest AICc values within each tissue region (indicated by horizontal dashed black line). Models used for further analysis below are indicated by red names.

Fig. 4: Visual comparison of the parameter maps from one participant (who showed intermediate chi² values, i.e. intermediate SNR), determined with four IVIM models (D^*-f-D, D^*-f-D₆, D₆^*e-f-D₆, and D₆^*-f₆-D₆ from top to bottom). Fractional anisotropy (FA) maps are displayed for all tensor parameters. In f, FA(f), D^*, and FA(D^*) maps, CSF voxels are set to 0.

Fig. 5: Quantitative results of the diffusion coefficient D, pseudo-diffusion coefficient D^*, the fractional anisotropies of D and D^* (the latter obtained with the model D₆^*e-f-D₆), and perfusion fraction f in NAWM, WMH, and GM obtained with the traditional 4-parameter IVIM model (D^*-f-D), the optimal model in NAWM (D^*-f-D₆), and the optimal model in WMH and GM (D₆^*e-f-D₆). The boxplots show the statistical distribution over 20 participants using the individual median values in each brain region.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

5175

DOI: https://doi.org/10.58530/2023/5175