5165
Simultaneous Estimation of Electrical Properties and Incident Fields Using Global Maxwell Tomography with B1+ and MR Signal Data
Jose E. C. Serralles1, Ilias I. Giannakopoulos2, Georgy D. Guryev1, Luca Daniel1, and Riccardo Lattanzi2
1Research Laboratory of Electronics (RLE), Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States
1Research Laboratory of Electronics (RLE), Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States
Synopsis
Keywords: Electromagnetic Tissue Properties, Electromagnetic Tissue Properties
We propose a novel approach to electrical property (EP) estimation that also estimates the incident fields generated by a coil, by solving a basis pursuit problem. We also propose a novel Global Maxwell Tomography (GMT) formulation that uses the MR signal instead of $$$B_1^+$$$. We tested our approach experimentally by reconstructing the average EP of a homogeneous cylinder. We obtained < 5% estimation error using only $$$B_1^+$$$ data obtained from MR Fingerprinting. We then estimated the receive sensitivity maps $$$B_1^-$$$ by using the new signal-based GMT.Introduction
The distribution of electrical properties (EP) of an object, namely relative permittivity $$$\epsilon_{R}$$$ and conductivity $$$\sigma$$$, dictates how the object interacts with electromagnetic fields. The ability to infer these EP from measured data would improve a myriad of applications, such as radiofrequency (RF) ablation, RF hyperthermia, and cancer detection1.The process of EP estimation is commonly referred to as inverse scattering or electrical property tomography (EPT). Most existing magnetic resonance (MR)-based EPT techniques rely on simplifying assumptions, such as the transceive phase approximation, limiting their applicability2,3. Global Maxwell Tomography (GMT) is a global formulation of EPT that requires RF coil incident fields and assumes that the coupling between the coil and body can be neglected, which is its only simplifying assumption1. In this work, we propose the use of basis pursuit with an electromagnetic basis to replace the coil model entirely. In addition, we propose a new cost function for GMT that uses MR signal data, rather than $$$B_1^+$$$. We demonstrate the effectiveness of our approach by estimating both the EP of a homogeneous cylinder and the coil's incident fields with a 7T experiment.
Methods
The traditional GMT optimization problem is described as:$$\begin{aligned}\min_{\epsilon\in\mathbb{C}^{N}}\quad & \sum_k \sum_l\left\| w_{kl}\odot \left[b_k^+\!\left(\epsilon\right)\odot\overline{b_l^+\!\left(\epsilon\right)}-\hat{b}_k^+\odot \overline{\hat{b}_l^+} \right] \right\|_2^2 \\ \textrm{s.t.}\quad & \text{Re}\!\left\{\epsilon\right\}\geq 1 \\ &\text{Im}\!\left\{\epsilon\right\}\leq 0\end{aligned}\tag{1}$$
The decision variables are complex relative permittivities, defined as $$$\epsilon=\epsilon_{\rm R}+\frac{\sigma}{j2\pi f\epsilon_0}$$$, where $$$f$$$ is the Larmor frequency. The cost function compares measured products of $$$\hat{b}_k^+$$$ with corresponding products of simulated $$$b_k^+$$$, computed using the (known) coil's incident fields with the EP estimate at the current iteration.
We surrounded the cylinder mask with volumetric current sources and approximated the mappings from sources to electric field $$$U_e$$$ and magnetic field $$$U_h$$$ using randomized SVD4. We then pose the task of estimating the coil's incident fields as a basis pursuit problem, using the same cost function as in Problem 1:
$$\begin{aligned}\min_{\alpha\in\mathbb{C}^{M\times N_{\rm tx}}}\quad &\sum_k\sum_l\left\|w_{kl}\odot \left[b_k^+(\alpha_k)\odot\overline{b_l^+(\alpha_l)}-\hat{b}_k^+\odot\overline{\hat{b}_l^+}\right]\right\|_2^2 \\ \textrm{s.t.}\quad &\text{Re}\!\left\{\alpha_{1,1}\right\}\geq 0 \\ &\text{Im}\!\left\{\alpha_{1,1}\right\}=0 \\\end{aligned}\tag{2}$$
The decision variables are the complex-valued basis coefficients $$$\alpha$$$, and the constraints help to reduce the size of the set of possible solutions. We perform this joint optimization over EP $$$\epsilon$$$ and basis coefficients $$$\alpha$$$ by first solving the basis pursuit problem given an initial guess of EP, and then solving the EP problem. We repeat this alternation, or "leap-frog", approach until we achieve the desired accuracy.
Given the challenges associated with the experimental measurement of $$$B_1^+$$$, we also propose a new MR signal-based GMT formulation:
$$\begin{aligned}\min_{\epsilon\in\mathbb{C}^{N}}\quad &\sum_k\sum_l\left\|w_{kl}\odot\left[s_{kl}(\epsilon)-\hat{s}_{kl}\right]\right\|_2^2 \\ \textrm{s.t.}\quad &\text{Re}\!\left\{\epsilon\right\}\geq 1 \\ &\text{Im}\!\left\{\epsilon\right\}\leq 0\\ \end{aligned}\tag{3}$$
where $$$s_{kl}$$$ denotes the MR signal associated with the transmit field $$$b_k^+$$$ and receive sensitivity map $$$b_l^-$$$. We also employ a corresponding basis pursuit problem:
$$\begin{aligned}\min_{\alpha\in\mathbb{C}^{M\times N_{\rm tx}}}\quad &\sum_k\sum_l\left\|w_{kl}\odot \left[s_{kl}(\alpha_k,\alpha_l)-\hat{b}_k^+\odot\overline{\hat{b}_l^+}\right]\right\|_2^2 \\ \textrm{s.t.}\quad &\text{Re}\!\left\{\alpha_{1,1}\right\}\geq 0 \\ &\text{Im}\!\left\{\alpha_{1,1}\right\}=0\\ \end{aligned}\tag{4}$$
To test our approach, we filled a cylinder with a solution of water and table salt (NaCl). We used a 7T ($$$f$$$ = 297.2MHz) 8-channel transmit/receive coil array5. We used MR Fingerprinting6 to obtain the 8 reference $$$|\hat{b}_k^+|$$$ maps. We then used the raw signals $$$s_{kl}$$$ to extract the relative phase information. We generated a numerical basis for the given geometry and solved the $$$b_1^+$$$-based optimization problems in an alternating fashion, starting from initial guesses of $$$\epsilon_{\rm R}=51$$$, $$$\sigma=0.13$$$S/m, $$$\alpha_{1,1}=1$$$, and 0 for the rest of the basis coefficients. We used $$$w_{kl} = |\hat{b}_k^+| \odot |\hat{b}_l^+|$$$ as the weights for the above equations and ran the leapfrog approach over the mean value of EP. Once we finished optimizing using $$$B_1^+$$$ data, we used the EP values to attempt to estimate the transmit and receive incident fields using the signal data.
Results & Discussion
Due to artifacts in the MR data, for this preliminary experiment we constrained all the EP to one value, from knowing that the phantom was homogeneous. We will remove this constraint in future experiments. Using a dielectric probe with expected error of 5%-10%, we measured the permittivity and conductivity to be 79.9 and 0.73S/m, respectively. Fig. 2 shows the evolution of permittivity and conductivity for various iterations. Fig. 3 shows the evolution of $$$|b_1^+|$$$ and relative phase between channels 1 and 2 along the same central slice. After 37 iterations, $$$\epsilon_{\rm R}$$$ converged to 81.2 and $$$\sigma$$$ converged to 0.71S/m, corresponding to 1.6% and 2.7% deviation, respectively, from measured probe values. Using the estimated EP, we inferred the receive coil sensitivities (Fig. 4).Conclusions
In this work, we proposed a new formulation of $$$B_1^+$$$-based GMT that completely abandons the coil model in favor a numerical basis. The reconstructed average EP values matched the values measured by the probe almost exactly. Removing the need of an accurate coil model simplifies GMT experiments and does not require worrying about the coupling between the body and the coil, which was neglected by the original GMT. This comes at the expense of computational cost. In addition, we also demonstrated that is possible to infer the transmit coil sensitivities using the new MR signal-based optimization approach. Future work will involve determining the root cause of artifacts in the experimental data and also speeding up the convergence of the alternating approach. Once we figure out those details, we will reconstruct objects that are not homogeneous.Acknowledgements
This work was supported by NIH R01 EB024536.References
- Serrallés, J.E., Giannakopoulos, I.I., Zhang, B., Ianniello, C., Cloos, M.A., Polimeridis, A.G., White, J.K., Sodickson, D.K., Daniel, L. and Lattanzi, R., 2019. Noninvasive estimation of electrical properties from magnetic resonance measurements via global Maxwell tomography and match regularization. IEEE Transactions on Biomedical Engineering, 67(1), pp.3-15.
- Mandija, S., Sbrizzi, A., Katscher, U., Luijten, P.R. and van den Berg, C.A., 2018. Error analysis of Helmholtz-based MR‐electrical properties tomography. Magnetic Resonance in Medicine, 80(1), pp.90-100.
- Balidemaj, E., van den Berg, C.A., Trinks, J., van Lier, A.L., Nederveen, A.J., Stalpers, L.J., Crezee, H. and Remis, R.F., 2015. CSI-EPT: A contrast source inversion approach for improved MRI-based electric properties tomography. IEEE transactions on medical imaging, 34(9), pp.1788-1796.
- Georgakis, I.P., Villena, J.F., Polimeridis, A.G. and Lattanzi, R., 2022. Novel Numerical Basis Sets for Electromagnetic Field Expansion in Arbitrary Inhomogeneous Objects. IEEE Transactions on Antennas and Propagation, 70(9), pp.8227-8241.
- Giannakopoulos, I.I., Serrallés, J.E., Daniel, L., Sodickson, D.K., Polimeridis, A.G., White, J.K. and Lattanzi, R., 2020. Magnetic resonance-based electrical property mapping using Global Maxwell Tomography with an 8-channel head coil at 7 Tesla: a simulation study. IEEE Transactions on Biomedical Engineering, 68(1), pp.236-246.
- Cloos, M.A., Knoll, F., Zhao, T., Block, K.T., Bruno, M., Wiggins, G.C. and Sodickson, D.K., 2016. Multiparametric imaging with heterogeneous radiofrequency fields. Nature communications, 7(1), pp.1-10.
Figures

Experimental setup. We used an 8-element transmit-receive triangular coil array (left) tuned at 297.2MHz (7T) to scan a homogeneous cylinder (right) filled with water and table salt (NaCl). We measured the phantom EP with a dielectric probe: the relative permittivity of the solution was 79.9 and the conductivity was 0.73 S/m.
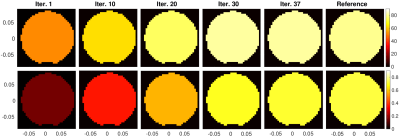
Evolution of relative permittivity $$$\epsilon_{\rm R}$$$ (top) and electric conductivity $$$\sigma$$$ (bottom) through the optimization, shown for the central transverse slice of the cylinder. Left-to-right: EP values after 1, 10, 20, 30, and 37 leap-frog iterations. The last column shows the EP values measured with a dielectric probe $$$\epsilon_{\rm R}$$$ values, top row, left-to-right: 51.2, 51.9, 63.2, 74.7, 80.3, 81.2. $$$\sigma$$$ values, bottom row, left-to-right: 0.133S/m, 0.154S/m, 0.358S/m, 0.571S/m, 0.69S/m, 0.71S/m.
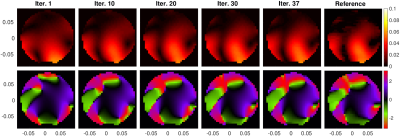
Evolution of the magnitude of the first transmit map $$$|b_1^+|$$$ (top) and relative phase between first and second maps $$$\phi_{12}$$$ (bottom) along the central transverse slice of the cylinder. Top/bottom, left-to-right: $$$|b_1^+|$$$/$$$\phi_{12}$$$ after 1, 10, 20, 30, 37 iter., and experimentally measured reference $$$|\hat{b}_1^+|$$$ and $$$\hat{\phi}_{12}$$$.

Evolution of the magnitude of the first receive sensitivity profile $$$|b_1^-|$$$. The outermost voxels are masked out to aid with visualization. Left-to-right: $$$|b_1^-|$$$ after 7, 11, 15, 19, 23, and 27 iter. of the leapfrog approach applied to the signal-based reconstruction approach. The $$$|b_1^-|$$$ profile focuses on one side of the cylinder as the iterations progress.
DOI: https://doi.org/10.58530/2023/5165