5164
Investigating Variable Density Sampling Patterns in Spiral Trajectories for use in MREPT1Computer Assisted Clinical Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany, 2Mannheim Institute for Intelligent Systems in Medicine, Medical Faculty Mannheim, Heidelberg University, Mannheim, Germany
Synopsis
Keywords: Electromagnetic Tissue Properties, Electromagnetic Tissue Properties
Magnetic Resonance Electrical Properties Tomography (MREPT) is used for obtaining conductivity by utilizing B1 phase images. In order to obtain B1 phase, different pulse sequences can be used. Among these, spiral trajectory based imaging has various advantages including high SNR efficiency and acquisition speed and was demonstrated in MREPT previously. In this work, to further improve spiral trajectory based imaging in MREPT, we investigate variable density sampling patterns. In vivo brain results indicate that conductivity images are quite robust with the choice of undersampling pattern and whole brain coverage can be completed under a minute with multiple averages.Introduction
Magnetic Resonance Electrical Properties Tomography (MREPT) aims to measure conductivity of the imaged object. It has been proven useful to diagnose various diseases, including ischemia and various types of tumours1-4. In order to obtain conductivity images, B1 phase information needs to be acquired. Various pulse sequences have been proposed to obtain B1 phase, with spin-echo and bSSFP based sequences being the most common5-9. However, spin-echo sequences require lengthy acquisition times and multi-acquisition schemes are necessary for bSSFP based sequences to avoid infamous banding artifacts.Center-out spiral-based acquisition schemes have been shown as a viable alternative for obtaining B1 information in MREPT10, owing to their high SNR efficiency, high acquisition speed, and robustness against motion artifacts. In order to further improve scan efficiency, undersampled acquisitions schemes can be considered. Since B1 phase maps are smooth, they contain mostly low frequency components, i.e. most of the information is concentrated close to the k-space center11. This can be exploited by utilizing variable density sampling patterns. Here, we propose the use of center-out variable density spiral trajectories to obtain B1 phase maps. We present in vivo results to demonstrate the potential of the proposed technique in conductivity imaging.
Methods
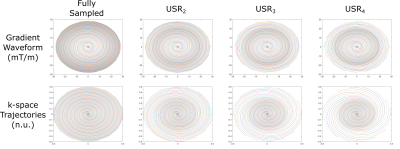
In vivo experiment was conducted on a 3T scanner (Magnetom Skyra, Siemens Healthineers, Germany), using a 16-channel head coil array. In vivo acquisitions were obtained from a healthy volunteer after obtaining written informed consent. In the experiment, a gradient-echo based pulse sequence with spiral trajectory was used with uniform and variable density patterns12. Archimedean spiral trajectories were implemented with a maximum gradient strength of 28 mT/m and maximum slew rate of 120 mT/m/ms.For variable density sampling, we divided the k-space into three zones: the center, transition zone and periphery. The center is always fully sampled, whereas the periphery is undersampled with different undersampling ratios of USRk with k=1,2,3,4 (USR1 denotes fully sampled data). During the transition zone, undersampling ratio changes linearly to between USR1 at center and USRk at the periphery. Implemented patterns with k-space trajectories and gradient waveforms are shown in Figure 1.
The volunteer was imaged using the following parameters: TE = 1.12 ms, TR(USR1/USR2/USR3/USR4) = 6.9/5.9/5.5/5.3 ms, FoV = 270 mm2, in-plane resolution = 2x2 mm, 32 slices, 16 averages, α=15°, slice thickness = 2.5 mm and 16 spiral interleaves. With these parameters, a single image can be obtain in less than 0.1 seconds, while total acquisition time is 56.5/48.3/45.1/43.4 seconds for USR1/USR2/USR3/USR4 respectively.
The missing k-space samples were recovered using the SPIRiT framework13. To this end, non-Cartesian SPIRiT was implemented in the image domain and reconstructions were obtained via iterative least squares (LSQR) algorithm. Phase images from different coils were combined using virtual reference coil approach14. Conductivity images were then obtained using a 3D phase-based convection-reaction-diffusion equation MREPT (cr-MREPT) technique with an artificial diffusion term15.
Results
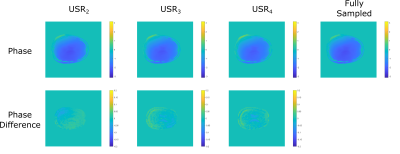
In Figure 2, phase images obtained using variable density sampling with different undersampling ratios and their differences with respect to phase image obtained from fully sampled data is shown. Maximum difference between phase images are 3.16°, 4.15°, and 4.52° for USR2, USR3 and USR4 respectively. As expected, the error increases as undersampling ratio increases, especially along the tissue boundaries; nevertheless the difference remains relatively low for all sampling patterns.In Figure 3, conductivity images obtained from phases with different undersampling ratios are shown, alongside with the bSSFP magnitude image as a reference. Conductivity images remain consistent across different undersampling ratios, indicating robustness against varying acceleration factors. Prominent structures like CSF are clearly distinguishable even with USR4, where the periphery of k-space is sparsely sampled.
Discussion and Conclusion
We have developed and demonstrated a spiral trajectory-based framework for rapid conductivity imaging with variable density sampling. Our results indicate that spiral trajectories can be further accelerated with variable undersampling without compromising the image quality. As such, conductivity images can be obtained successfully even with the acquisition time of less than a minute for whole brain coverage.Due to gradient imperfections, perturbations in k-space trajectories are to be expected, which lead to image artifacts. Since the differences between the prescribed and measured trajectories accumulate throughout the acquisiton16, shortening the length of the acquisition can help reduce these artifacts. Therefore, undersampling the periphery of the k-space may suppress artifacts stemming from system imperfections.
While further studies are warranted, this framework can be used to shorten total acquisition time in conductivity imaging. Our initial results indicate that in vivo conductivity images can be acquired successfully under a minute. Overall, our framework can further reduce the scan time without compromising image quality, and therefore can improve the utility of MREPT imaging.
Acknowledgements
No acknowledgement found.References
1. Tha, Khin K., et al. "Higher Electrical Conductivity of Liver Parenchyma in Fibrotic Patients: Noninvasive Assessment by Electric Properties Tomography." Journal of Magnetic Resonance Imaging, vol. 54, no. 5, 2021, pp. 1689-1691.
2. Balidemaj, Edmond, et al. "Feasibility of Electric Property Tomography of pelvic tumors at 3T." Magnetic Resonance in Medicine, vol. 73, no. 4, 2014, pp. 1505-1513.
3. Shin, Jaewook, et al. "Initial study on in vivo conductivity mapping of breast cancer using MRI." Journal of Magnetic Resonance Imaging, vol. 42, no. 2, 2014, pp. 371-378.
4. Gurler, Necip, et al. "Application of generalized phase based electrical conductivity imaging in the subacute stage of hemorrhagic and ischemic strokes." Proceedings of the 24th Annual Meeting of ISMRM; 2016; Singapore, Singapore.
5. Hafalir, Fatih S., et al. "Convection-Reaction Equation Based Magnetic Resonance Electrical Properties Tomography (cr-MREPT)." IEEE Transactions on Medical Imaging, vol. 33, no. 3, 2014, pp. 777-793.
6. Shin, Jaewook, et al. "Fast Spin Echo Imaging-Based Electric Property Tomography With K-Space Weighting via T2 Relaxation (rEPT)." IEEE Transactions on Medical Imaging, vol. 36, no. 8, 2017, pp. 1615-1625.
7. Ozdemir, Safa, et al. "bSSFP phase correction and its use in magnetic resonance electrical properties tomography." Magnetic Resonance in Medicine, vol. 81, no. 2, 2018, pp. 934-946.
8. Ozdemir, Safa, et al. "Estimation of transceive phase via LORE-GN algorithm and its use in MREPT." Proceedings of the 27th Annual Meeting of ISMRM; 2019; Montreal, Canada.
9. Gavazzi, Soraya, et al. "Transceive phase mapping using the PLANET method and its application for conductivity mapping in the brain." Magnetic Resonance in Medicine, vol. 83, no. 2, 2019, pp. 590-607.
10. Ozdemir, Safa, et al. "Investigating Spiral Trajectories for Sub-second Conductivity Imaging in MREPT." Proceedings of the 31th Annual Meeting of ISMRM; 2022; London, UK.
11. Lustig, Michael, et al. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic Resonance in Medicine, vol. 58, no. 6, 2007, pp. 1182-1195.
12. Pipe, James G., et al. "Spiral trajectory design: A flexible numerical algorithm and base analytical equations." Magnetic Resonance in Medicine, vol. 71, no. 1, 2013, pp. 278-285.
13. Lustig, Michael, and John M. Pauly. "SPIRiT: Iterative self‐consistent parallel imaging reconstruction from arbitrary k ‐space." Magnetic Resonance in Medicine, vol. 64, no. 2, 2010, pp. 457-471.
14. Parker, Dennis L., et al. "Phase reconstruction from multiple coil data using a virtual reference coil." Magnetic Resonance in Medicine, vol. 72, no. 2, 2013, pp. 563-569.
15. Gurler, Necip, and Yusuf Z. Ider. "Gradient‐based electrical conductivity imaging using MR phase." Magnetic Resonance in Medicine, vol. 77, no. 1, 2016, pp. 137-150.
16. Campbell-Washburn, Adrienne E., et al. "Real-time distortion correction of spiral and echo planar images using the gradient system impulse response function." Magnetic Resonance in Medicine, vol. 75, no. 6, 2015, pp. 2278-2285.
Figures