5163
Implicit Regularization for Improving Phase-based EPT with Stein’s Unbiased Risk Estimator1Department of Electrical and Electronic Engineering, Yonsei University, Seoul, Korea, Republic of
Synopsis
Keywords: Electromagnetic Tissue Properties, Electromagnetic Tissue Properties
Phase-based EPT algorithm is extremely sensitive to noise. Although various denoising algorithms have been introduced to suppress noise amplification, residual artifact cause instability conductivity error or broadening boundary artifact. In this work, we propose a novel generative network trained with Stein’s unbiased risk estimator under the purely unsupervised learning framework, which improve the performance of phase-based conductivity reconstruction algorithms. In addition, the proposed method does not need any dataset for training neural network and not require any prior information for designing explicit regularization.Introduction
Electrical properties tomography (EPT)1 is a non-invasive technique that allows to estimate EPs (electrical properties) value in MR system. In particular, phase-based EPT is sensitive to noise due to the computation of the Laplacian operator. To address such noise amplification problems, many studies may be preferred to use image filters or optimize the parameters of reconstruction algorithms, however, there are still limitations (e.g., blurring, texture noise, and staircasing artifact). As an alternative to these noise suppression methods, regularization process2,3,4 have been investigated for phase denoising and have shown superior results compared to linear filtering results. However, they still have drawbacks of requiring prior information from noiseless data to design explicit regularizations.Since prior information is generally unavailable or unknown, the design of proper regularization which can represent the generic prior of natural image may be difficult to use while estimating the optimal parameters. To deal with this problem, The inductive bias of untrained over-parameterized CNN which can provide implicit prior5 , thereby replacing the explicit regularization, has been suggested. Although this method does not need any degradation process, the overfitting problem is still challenging due to the use of MSE loss function. On the other hand, the Stein’s unbiased risk estimator (SURE)6 has been proposed to avoid the overfitting problem in the Gaussian noise scenario, which is consistent with the MRI noise distribution in real and imaginary domains7.
In this study, we propose a new pre-processing denoiser, and evaluate the performance of proposed method compared with various explicit regularization methods in simulated cylinder and brain phantoms as well as turbo spin-echo (TSE) in-vivo data. Each denoising result was investigated for both B1 phase and phase-based EPT maps, and various phase-based conductivity reconstruction methods4,8,9 were used for the observations.
Theory
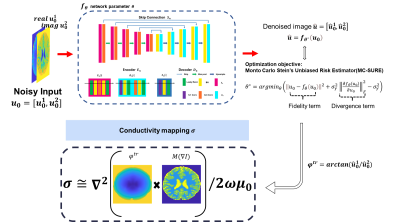
Implicit regularization for the forward model of conductivity reconstruction with SURE loss:$$\theta^{*}=argmin_{\theta}(\parallel u_{0}-f_{\theta}(u_{0}) \parallel^{2}+\sigma_\lambda^2\parallel\frac{\partial f_{\theta}(u_{0}) }{\partial u_{0}}\parallel_F^2 -\sigma_\lambda^2 ) [1]$$
$$\widehat{\sigma}=\phi(arctan[f_{\theta^{*}}(u_{0})]*M(\triangledown I))[2]$$
$$$u_{0}\in R^{H\times W\times2}$$$ is concatenation of real and imaginary images, which are corrupted by Gaussian noise with std $$$\sigma_{\lambda}$$$. $$$f_{\theta}(\cdot)$$$ is ‘hourglass’ convolutional neural network as shown in Figure 1. The minimizer $$$\theta^{*}$$$ is obtained using an ADMM optimizer, starting from a random initialization of the parameters $$$ \theta$$$ with the SURE loss. The additional divergence term is approximated by Monte Carlo method6. $$$\phi(\cdot) $$$ is conductivity mapping function, and $$$M(\triangledown I)$$$ represents the mask that different anatomical regions for reducing boundary artifact. Once given the optimized parameter $$$ \theta^{*}$$$ , the denoised real and imaginary images can be determined by $$$ f_{\theta^{*}}(u_{0})$$$ . Then forward conductivity mapping function was computed to evaluate the conductivity value.
Method
[Simulation data]To synthesize SE images, B1+ and B1- fields were calculated inside a birdcage coil, resonating at 128MHz (i.e. 3T MRI) by the finite-difference time-domain EM simulation program (Sim4Life, Zurich Med Tech, Zurich, Switzerland)10,11. Then, synthetic SE images were generated by using the signal and Bloch equations (resolution=1x1mm, slice thickness=2mm).
[In-vivo]
In-vivo data: TSE data were acquired at 3T: 1 healthy volunteer (Tim Trio, Siemens Healthineers: TR/TE=4500/77ms, resolution=0.5x0.5mm, slice thickness=3mm, averages = 8, Total scan time =14:30min)
Result
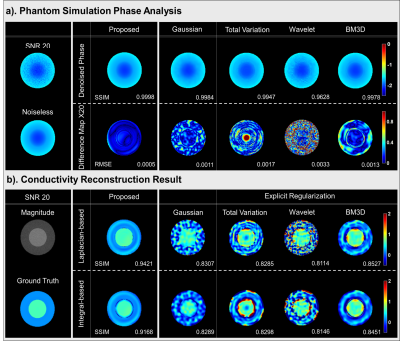
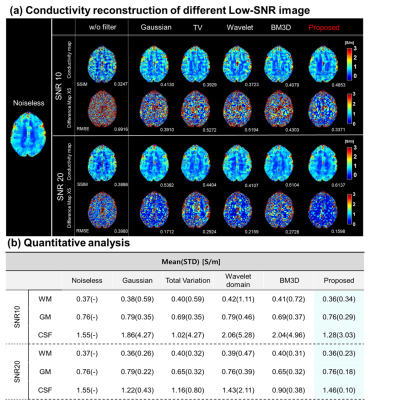
Figure 2 shows proposed methods compared with other methods on phantom simulation data to investigate the denoising performance of different methods in homogenous regions. Two phase-based EPT reconstruction techniques8 are utilized to calculate conductivity map. Compared to GTC as a reference, the proposed method shows more stable conductivity values, especially in homogenous regions. Furthermore, it can compensate errors in inner and outer interface region.Figure 3(a) shows results where the proposed method was tested on different SNR brain simulation data. Compared to other methods, the proposed method shows less conductivity error as shown in conductivity difference map. In Figure 3(b), we can obviously observe that the proposed method not only reconstructs stable conductivity value but achieves closest mean values in WM, GM, CSF, respectively, at different low-SNR levels.
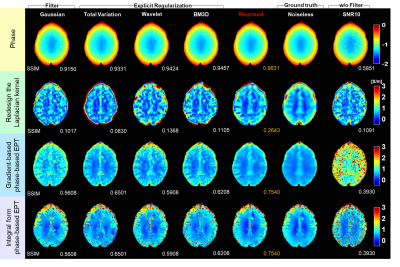
Figure 4 shows the results for various denoising methods by using various phase-based conductivity reconstruction algorithms4,8,9 on brain simulation data. The proposed method achieved highest SSIM value among the denoising methods with various conductivity reconstruction algorithms.
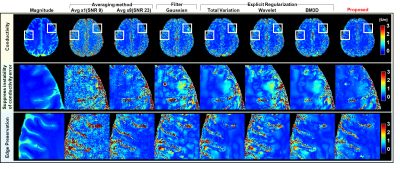
Figure 5 shows the conductivity maps with various denoising methods on in-vivo data. The proposed method shows not only reconstruct stable conductivity value but shows well edge-preservation in the magnified white boxes compared to other methods.
Conclusion
In this study, we propose a novel generative network trained with Stein’s unbiased risk estimator under the purely unsupervised learning framework, which improve the performance of phase-based conductivity reconstruction algorithm in comparison with conventional algorithms. The main advantages of the proposed method are dataset-free during training and not requiring knowledge of noiseless images to design explicit regularization and construct dataset. In addition, in this proposed regularization procedure, the use of SURE allowed to prevent overfitting problems that can occur due to the unknown of noiseless information. It has been shown that the proposed method not only suppresses instability due to noise amplification, but also reduces boundary artifacts of simulated phantom and in-vivo datasets.Acknowledgements
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (NRF-2019R1A2C1090635)References
[1] Voigt. et al.,Quantitative conductivity and permittivity imaging of the human brain usingelectrical properties tomography. Mag. Reson. Med., Vol 66(2), 2011,456-466.
[2] K. M. Ropella and D. C. Noll, “A regularized, model-based approach to phase-based conductivity mapping using MRI,” Magn.Reson. Med., vol. 78, no. 5, pp. 2011–2021, Nov. 2017.
[3] Borsic, A., Perreard, I., Mahara, A., and Halter,R. J. (2015). An inverse problems approach to MR-EPT image reconstruction. IEEE Trans. Med. Imaging 35, 244–256.doi: 10.1109/tmi.2015.2466082
[4] Shin J., Kim J.H.,Kim D.H. Redesign of the Laplacian Kernel for Improvements in Conductivity Imaging Using MRI. Magn.Reson. Med. 2019;81:2167–2175.doi:10.1002/mrm.27528.
[5] Ulyanov, D., Vedaldi, A., & Lempitsky, V.(2018). Deep image prior. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 9446-9454).
[6] S. Ramani, T. Blu, and M. Unser. Monte-carlo sure: A blackbox optimization of regularization parameters for general denoising algorithms. TIP, 2008
[7] Lysaker M.Lundervold A. and Tai X.-C, “Noise removal using fourth-order partial differential equations with applications to medical magnetical resonance imagesin space and time”, IEEE Trans on Image Processing..12,12 2003, pp. 1579-1590
[8] Anita Karsa. et al., New approaches for simultaneous noise suppression and edge preservation to achieve accurate quantitative conductivity mapping in noisy images. In Proc. 30th Annu.Meet.ISMRM
[9] N. Gurler and Y. Z. Ider, “Gradient-based electrical conductivity imaging using phase,” Magn. Reson. Med., vol. 77, no. 1, pp. 137–150, Jan. 2017
[10] Christ A, Kainz W, Hahn EG, et al. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2009;55:N23.
[11] Gosselin M-C, Neufeld E, Moser H, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys Med Biol. 2014;59:5287.
Figures