Synopsis

Keywords: Elastography, White Matter

Anisotropic MRE has shown some promise in estimating mechanical properties of fiber-reinforced biological tissues. However, these methods are restricted to modeling a single fiber and ignores complexity that occurs such as regions of brain white matter with crossing fibers. Here we implement an inversion algorithm capable of modeling material with two fiber directions obtained from diffusion MRI in order to reduce model data mismatch and provide fiber-specific properties, which may show promise in correlating with brain health and function. Performance of this algorithm is demonstrated in simulation and in vivo brain data and compared with one-fiber and zero-fiber (isotropic) inversions.

Introduction

MR elastography exploits the premise that microscale cellular changes due to disease processes cause changes in the continuum mechanical properties of tissue, and images of these properties can be inferred from MR-measured displacements of vibrating tissue. Selecting a continuum mechanical model is a necessary step to balance simplicity and complexity, where simpler models have fewer unknown parameters requiring estimation at the cost of potential modeling errors, and more complex models can reduce model data mismatch by accurately representing the true mechanical behavior of tissue but place greater demands on the data due to the wider spectrum of estimated properties. Many successful applications with a simple viscoelastic model have been demonstrated, however, recent successes with a transverse isotropic model¹ of tissues reinforced by aligned fiber tracts suggest we may not have reached the limit of achievable complexity. The next step up in anisotropic model complexity is a crossing fiber model which captures tissues with two separate fiber families passing through at different angles. This model is relevant in brain where up to 40% of white matter has crossing fibers, and muscle where fibers are arranged in sheets.

Methods

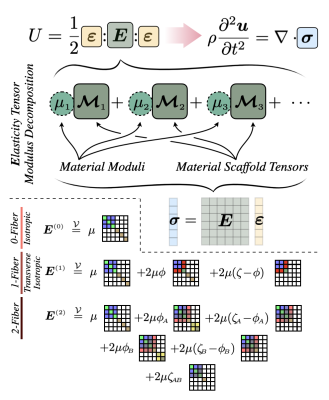
Both mechanical and diffusion anisotropy occur due to preferentially aligned directions in the tissue microstructure, so it can be assumed that the fiber maps from DTI also correspond to the preferred directions of mechanical anisotropy. DTI can image the local directions of crossing fibers, and these fiber maps form the basis of our two-fiber family (2FF) mechanical model.

To derive a mechanical model, the elasticity tensor can be constructed in the lab coordinate frame by associating a moduli with each possible irreducible representation constructed from the scalar and tensor degrees of freedom and any privileged directions (i.e. direction of fiber families), together with the volumic-isochoric decomposition which provides a convenient pathway to avoid numerical issues near-incompressible finite element models. Using zero privileged directions gives two moduli and reproduces the commonly used isotropic viscoelastic model. Adding one privileged direction yields an additional two moduli and a form which is identical to the single fiber transverse isotropic model which has been recently employed in MRE. Finally, adding a second fiber family yields an additional 4 moduli and forms our two-fiber family (2FF) model. Importantly, this hierarchical approach (illustrated in figure 1) provides a simple pathway for a future multi-model anisotropic MRE inversion where isotropic parameters are recovered where no DTI fibers are found, single fiber transverse isotropic parameters in regions of one fiber, and 2FF parameters in regions with crossing fibers. In this work, we investigate recovering 2FF parameter across the whole brain as a first step in the multi-model development process. Isotropic inertial damping is implemented with a complex-valued density and real-valued moduli to restrict the number of estimated parameters to 8.
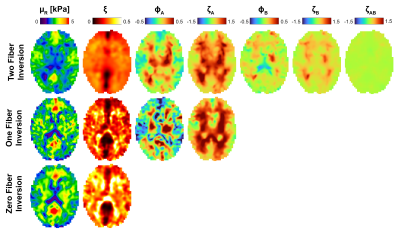
Inversion protocol: Six real-valued 2FF moduli, μ₁-μ₆ , and an imaginary density, ρ_{I ⁽²⁾}, were reconstructed using a finite element-based nonlinear inversion algorithm from the AP and LR displacement fields (μ₇ was not reconstructed to avoid ambiguity in computing fiber interaction moduli). Zero-fiber isotropic NLI and one-fiber TI-NLI were also run on the same data for comparison. Constant density of 1000kgm^-3 and nearly incompressible bulk modulus of 10⁹Pa were specified. Substrate shear modulus, μ, Fiber shear anisotropy, φ_A/B, tensile anisotropy, ζ_A/B, and interaction moduli, ζ_AB, analogous to TI-NLI was computed using the relationships in figure 1.
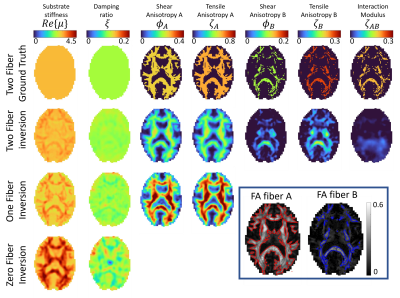
Simulated experiments: A realistic brain simulation generated form in vivo MRE³ with properties defining three classes of tissue, 0 fibers for FA_A and FA_B < 0.15, one fiber for FA_A>0.15 & FA_B<0,15, and two fibers for FA_A>0.15 and FA_B>0,15. Zero, one and two-fiber nonlinear inversion (NLI) property recovery algorithms were run to investigate performance when regions of different fiber counts are present.
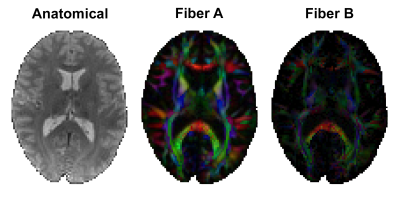
In vivo imaging protocol: MRE and diffusion MRI data was collected and reported in [Smith 2022]⁴. Multi-excitation MRE acquisition at 2 mm isotropic resolution generated two displacement fields: with anterior-posterior left-right vibrations, both at 50 Hz. Diffusion data at 1.5 mm resolution (128 directions, b = 1500 and 3000 s/mm2) was processed with bedpostx in FSL to estimate up to two axonal fiber directions (Figure 3) in each voxel^5,6. Here we show data on a 26 yo female subject.

Results and Discussion

The new two-fiber model does show some promise, with reasonable performance in the simulated data shown in figure 2, and in vivo images in figure 4 show structure and symmetry. The loss of resolution in the moving from the one-fiber to two-fiber models shown in figure 4 suggests we are getting close to the limit of achievable complexity for MRE in these anisotropic models. A multi-model approach where the number of fibers varies based on DTI two-fiber fractional anisotropy maps may help by reducing unnecessary unknowns where they are not required. The hierarchical structure of the model presented here will be valuable as elasticity matrix terms can be truncated when a fiber isn't present.

Acknowledgements

NIH/NIBIB grant R01-EB027577.