5150
Transversely Isotropic MR Elastography with a Power Law Multi-Frequency Reconstruction
1Biomedical Engineering, University of Delaware, Newark, DE, United States, 2Département de Génie Mécanique, Université de Sherbrooke, Sherbrooke, QC, Canada, 3Thayer School of Engineering, Dartmouth College, Hanover, NH, United States, 4McKelvey School of Engineering, Washington University in St. Louis, St. Louis, MO, United States
Synopsis
Keywords: Elastography, Brain
This study combined multiexcitation MRE (ME-MRE), and multifrequency MRE (MF-MRE) with a transversely isotropic nonlinear inversion (TINLI) and axonal fiber directions from diffusion tensor imaging to investigate anisotropic and frequency-dependent material properties simultaneously. These preliminary results show that multifrequency-TINLI MRE can be readily applied to in vivo human data at distinct frequencies.
Introduction
Magnetic resonance elastography (MRE) is a noninvasive imaging technique that produces quantitative maps of tissue mechanical properties, such as shear stiffness, for soft tissues in humans, including the brain1. These mechanical properties capture information on the composition and organization of the brain tissue and are sensitive to microstructural changes that occur with age and neurological diseases2. Our group developed a multiexcitation MRE protocol (ME-MRE)3–5 and a transversely isotropic nonlinear inversion (TINLI)6–8 to estimate anisotropic mechanical properties in human white matter tracts. We have demonstrated that ME-MRE generates waves sufficient for repeatable anisotropic inversions in a group of young healthy volunteers5,9. However, generating more than two distinct wave fields within the constraints of a typical MRI head coil is challenging, if more than one driver is required. To produce a more diverse set of wavefronts, multifrequency MRE (MF-MRE) can generate wave fields with the differing propagation and polarization characteristics that are necessary for anisotropic property estimation10. Moreover, Guo et al.11 estimated anisotropic properties of leg muscles via MF-MRE. Here, we use MF-MRE data to estimate anisotropic properties of brain tissue using TINLI. Notably, we modeled both anisotropic and frequency-dependent behavior of brain tissue simultaneously. Previous MF-MRE studies demonstrated that the complex shear modulus of soft biological tissues follows a power-law frequency dependence12. However, this frequency-dependent behavior has not been implemented in previous anisotropic inversions.Methods
Image Acquisition:Two healthy young (ages: 23, 26) participants completed a multiexcitation and multifrequency MRE protocol using a 20-channel head coil in a Siemens 3T Prisma Scanner, which recorded MRE displacements in the anterior-posterior (AP) and left-right (LR) directions. MRE scans were collected in the AP direction at 30, 40, 50, 60 ,70 Hz, and one 50 Hz LR scan was collected to mimic the multiexcitation protocol4,5. MRE scans were acquired with a 3D multiband, multishot, spiral MRE sequence13,14 that images whole-brain displacement at 2 mm isotropic resolution (240x240x128 mm FOV, 64 slices, TR/TE = 2240/76 ms). Auxiliary scans for all data sets included DTI at 1.5 mm3 (210x240x138 FOV, 92 slices, TR/TE = 3520/95.2 ms), from which the primary diffusion direction was extracted, and T1-weighted MPRAGE at 0.9 mm3 for tissue segmentations.
Multifrequency and TINLI Inversion:
Two different formulations were used to estimate the MRE parameters of interest. The TINLI algorithm combines AP and LR wave motion fields at the frequency of interest along with the primary eigenvector from diffusion, locally assumed to be the primary fiber direction, to recover the substrate shear modulus , shear anisotropy $$$\phi = \mu_{1}/\mu_{2} -1$$$, and tensile anisotropy $$$\zeta = E_{1}/E_{2}-1$$$ as shown in Fig. 1A for a single healthy subject (age: 26). For multifrequency inversions (Fig. 1B), real and imaginary shear moduli were modeled as frequency dependent through $$$\mu_{R}(\omega) = \theta_{0R}\cdot \omega^{\alpha_{R}}$$$ and $$$\mu_{I}(\omega) = \theta_{0I}\cdot \omega^{\alpha_{I}}$$$ 15. MRE data was skull stripped16 and segmented into gray matter (GM) and white matter (WM) regions using FAST in FSL17 and the WFU PickAtlas18 to isolate the cerebrum.
Results
MRE parameter reconstructions for a single healthy subject (age: 23) are summarized in Fig. 2. Multi-frequency MRE inversions not considering frequency-dependence (i.e. $$$\alpha = 0$$$, Column 3) produced TI properties consistent with ME-MRE inversions (Column 2). Frequency-dependent shear stiffness shown at 50 Hz in column 4 is elevated slightly, $$$\mu_{MF,WM}=3.48 kPa$$$ but showed good contrast recovery relative to standard TI-NLI $$$\mu_{ME,WM}=2.58 kPa$$$. Conversely, MF-MRE produced lower shear and tensile anisotropy ($$$\phi_{MF,WM}=-0.09$$$, $$$\zeta_{MF,WM}=0.46$$$), but similar structural contrast relative to single and multiexcitation inversions ($$$\phi_{ME,WM}=-0.01$$$, $$$\zeta_{ME,WM}=0.67$$$). Specifically, we see positive shear anisotropy in the deep white matter tracts, and positive tensile anisotropy occurred throughout the white matter. Fig. 3 reports average values in GM and WM regions for multifrequency versus multiexcitation data. In both regions, MF-MRE shear stiffness was higher and anisotropy parameters were lower relative to the ME-MRE inversion. Both subjects had similar values overall across the parameters.Discussions and Conclusions
Results demonstrate the feasibility of recovering both anisotropic and frequency-dependent mechanical properties in the human brain simultaneously using multifrequency MRE coupled with TINLI. Shear and tensile anisotropy maps were reconstructed with good contrast and are comparable with our multiexcitation MRE results. Estimated negative values of φ may stem from model-data mismatch at the grey/white matter boundaries where tissue properties can change abruptly from anisotropic to isotropic and a strong fiber direction is lacking. Further tuning of the frequency dependent inversion will be needed to generate accurate property reconstructions in the white matter tracts using the multifrequency MRE approach. In future studies, this novel approach will be performed on a larger cohort of subjects, to estimate frequency dependent and anisotropy parameters within individual white matter tracts.Acknowledgements
This research was supported by NIH grants R01-EB027577, R01-AG058853, and U01-NS112120.
References
1. Hiscox, L. V et al. Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications. Phys. Med. Biol. 61, R401–R437 (2016).
2. Murphy, M. C., Huston, J. 3rd & Ehman, R. L. MR elastography of the brain and its application in neurological diseases. Neuroimage 187, 176–183 (2019).
3. Anderson, A. T. et al. Observation of direction-dependent mechanical properties in the human brain with multi-excitation MR elastography. J. Mech. Behav. Biomed. Mater. 59, 538–546 (2016).
4. Smith, D. et al. Multi-Excitation MR Elastography of the Brain: Wave Propagation in Anisotropic White Matter. J. Biomech. Eng. 142, 710051–710059 (2020).
5. Caban-Rivera, D., Smith, D., Kailash, K., Okamoto, R., McGarry, M., Williams, L., Guertler, C., McIlvain, G., Sowinski, D., Houten, E. Van, Paulsen, K., Bayly, P., Johnson, C. Multi-Excitation Actuator Design for Anisotropic Brain MRE. 29th Annu. Meet. Int. Soc. Magn. Reson. Med. May 15-20, 2021 (2021).
6. McGarry, M. D. J. et al. Model-Based Heterogeneous Transverse Isotropic MR Elastography Inversion for Brain Tissue with Aligned Fiber Tracts. 28th Annu. Meet. Int. Soc. Magn. Reson. Med.
7. McGarry, M. D. J. et al. A heterogenous, time harmonic, nearly incompressible transverse isotropic finite element brain simulation platform for MR elastography. Phys. Med. Biol. (2020) doi:10.1088/1361-6560/ab9a84.
8. McGarry, M. et al. Mapping Heterogenous Anisotropic Tissue Mechanical Properties with Transverse Isotropic Nonlinear Inversion MR Elastography. Med. Image Anal. 78, 102432 (2022).
9. Smith, D. R. et al. Anisotropic mechanical properties in the healthy human brain estimated with multi-excitation transversely isotropic MR elastography. Brain Multiphysics 3, 100051 (2022).
10. Tweten, D. J., Okamoto, R. J. & Bayly, P. V. Requirements for accurate estimation of anisotropic material parameters by magnetic resonance elastography: A computational study. Magn. Reson. Med. 78, 2360–2372 (2017).
11. Guo, J., Hirsch, S., Scheel, M., Braun, J. & Sack, I. Three-parameter shear wave inversion in MR elastography of incompressible transverse isotropic media: Application to in vivo lower leg muscles. Magn. Reson. Med. 75, 1537–1545 (2016).
12. Sack, I., Jöhrens, K., Würfel, J. & Braun, J. Structure-sensitive elastography: on the viscoelastic powerlaw behavior of in vivo human tissue in health and disease. Soft Matter 9, 5672–5680 (2013).
13. Johnson, C. L., Holtrop, J. L., Anderson, A. T. & Sutton, B. P. Brain MR Elastography with Multiband Excitation and Nonlinear Motion-Induced Phase Error Correction. 24th Annu. Meet.
14. McIlvain, G., Cerjanic, A. M., Christodoulou, A. G., McGarry, M. D. J. & Johnson, C. L. OSCILLATE: A low-rank approach for accelerated magnetic resonance elastography. Magn. Reson. Med. 88, 1659–1672 (2022).
15. Testu, J. et al. Viscoelastic power law parameters of in vivo human brain estimated by MR elastography. J. Mech. Behav. Biomed. Mater. 74, 333–341 (2017).
16. Smith, S. M. Fast robust automated brain extraction. Hum. Brain Mapp. 17, 143–155 (2002).
17. Zhang, Y., Brady, M. & Smith, S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 20, 45–57 (2001).
18. Maldjian, J. A., Laurienti, P. J., Kraft, R. A. & Burdette, J. H. An automated method for neuroanatomic and cytoarchitectonic atlas-based interrogation of fMRI data sets. Neuroimage 19, 1233–1239 (2003).
Figures
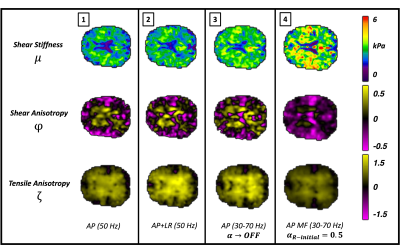
Figure 2. Reconstructed property map comparison across inversion schemes for a single healthy young adult (age: 23). Each column represents parameters reconstructed separately. Column 4 reports the novel MF-TINLI inversion results, which demonstrates good structural contrast recovery, positive anisotropies in the central tracts, and slightly elevated shear stiffness.
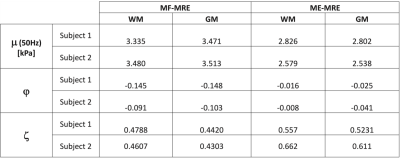
Figure 3. Average transversely isotropic nonlinear inversion (TINLI) parameters in GM and WM regions for multifrequency versus multiexcitation data. In both regions, MF-MRE shear stiffness was higher and anisotropy parameters were lower relative to the ME-MRE inversion. The two inversions show slightly lower anisotropy in GM relative to WM. Subject 1 (age 26), Subject 2 (age 23).
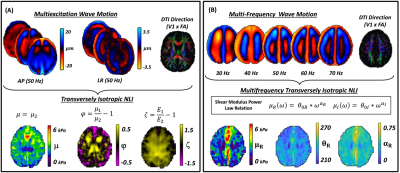
Figure 1. Multiexcitation and multifrequency transversely isotropic (TI) Inversion for a single adult. Motion fields acquired through multiexcitation (A) or multifrequency (B) are combined with the axonal fiber direction and are inverted using nonlinear inversion (NLI). Substrate shear modulus (plotted as shear stiffness), and two anisotropy parameters capture the relative stiffness of white matter tracts in directions parallel to versus perpendicular to the diffusion direction. In MF-TINLI, the real and imaginary shear components (at 50 Hz) are estimated simultaneously.