5142
Reconstruction of Dynamic MRI Tensor Data Using Frequency Low-rank and Sparsity Prior1Center for Biomedical Imaging Research, Tsinghua University, Beijing, China
Synopsis
Keywords: Heart, Image Reconstruction
Obtaining high spatial and temporal resolution image in dynamic magnetic resonance imaging is a huge challenge. It is effective to use low-rank and sparse prior jointly for dMRI reconstruction. However, the models represented the tensor data into a matrix, which can not completely explore the spatiotemporal correlation information. Besides, using nuclear norm as convex surrogate of the rank function to enforce the low-rank, which may lead to the sub-optimal result. Hence, we proposed the piecewise frequency tensor nuclear norm in the low-rank and joint sparse prior to reconstructed data. The proposed method was tested in cardiac cine and perfusion data.Introduction
Dynamic magnetic resonance imaging (dMRI) plays an important role in clinical applications1-3. However, due to the limitation of the Nyquist criterion, obtaining high spatial and temporal resolution image in dMRI is a huge challenge. It is effective to use low-rank prior and sparse prior jointly for reconstruction. For example, Compress sensing exploited sparse representation of dMRI in some known transform domains for reconstruction 4-7. Although these research findings showed that the model was particularly well suited for reconstructing dMRI, there were limitations of the above methods. The data were acquired in spatiotemporal dimension and hence their reconstruction involved analyzing high-order data that were known as tensors8,9. While the above models represented the tensor data into a matrix and solved by matrix correlation operation, which can not completely explore the inherent spatiotemporal correlation information. Besides, using nuclear norm as convex surrogate of the rank function to enforce the low-rank may lead to the sub-optimal result10,11. Hence, we proposed the piecewise frequency tensor nuclear norm to recover more information from the observed data in the low-rank and joint sparse prior to reconstructed data. The model can use the information in the frequency domain as a priori assisted reconstruction. The proposed method was tested in cardiac cine and perfusion data.Method
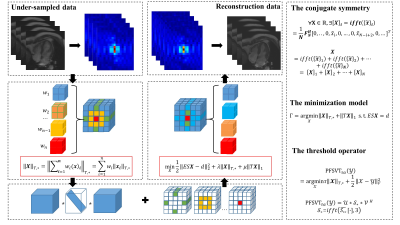
Theory:Given a tensor $$$X=[{{x}_{1}},{{x}_{2}},\cdots ,{{x}_{N}}]\in {{\mathbb{R}}^{P\times M\times N}}$$$,then its Fourier change is $$$\tilde{X}=fft(X),X=ifft(\tilde{X})$$$. According to the conjugate symmetry of the frequency domain, the following can be obtained:$${\left\{ {\tilde X} \right\}_n} = \left\{ {\begin{array}{*{20}{c}} {\left( {{{\tilde x}_n}} \right),n = 1\;or\;n = N - n + 2}\\ {\left( {{{\tilde x}_n},{{\tilde x}_{N - n + 2}}} \right),otherwise} \end{array}} \right.\tag{1}$$According to above theory, the proposed piecewise frequency tensor nuclear norm is defined as follows:$${\left\| {\left. X \right\|} \right._{T,*}} = \left\| {\left. {\mathop \sum \nolimits_{i = 1}^n {w_i}{{\left( x \right)}_i}_{T,*}} \right\|} \right. = \mathop \sum \limits_{i = 1}^n {w_i}{\left\| {\left. {{x_i}} \right\|} \right._{T,*}}\tag{2}$$where $$${x_i}$$$ is the ith forward slice matrix of tensor $$$X$$$,$$$\;{w_i}$$$ is piecewise frequency factor, which helped to improve the reconstruction effect by using different weights on the high and low frequency slices. We combined with the above norm and sparse prior minimization model:$$\mathop {\min }\limits_X \frac{1}{2}\left\| {\left. {ESX - d} \right\|} \right._2^2 + \lambda {\left\| {\left. X \right\|} \right._{T,*}} + \mu {\left\| {\left. {TX} \right\|} \right._1}\tag{3}$$where $$$T$$$ is a sparsifying transform, $$$E$$$ is the encoding operator, $$$S$$$ is sensivivty map and $$$d$$$ is the under-sampled data. The parameters $$$\lambda $$$ and $$$\mu $$$ are used to trade off data consistency. We solve the optimization problem in Eq. (3) using iterative soft-threshold algorithm. Tensor singular value threshold operator can solve the piecewise frequency tensor nuclear norm according to ref12 for solving. The whole process is shown in FIG.1.Retrospective experiments: The datasets included the ten public cine data13 and two cardiac perfusion MRI data5,6. The datasets were all fully sampled, and then simulated under-sampling processing are carried out.
Compared methods & Image Reconstruction: Image reconstruction was performed in MATLAB R2017a compare with some popular methods including k-t SPARSE SENCE5 and L+S method7.Reconstruction performance was evaluated using the Peak Signal to Noise Ratio (PSNR)、Root Mean Squared Error (RMSE) and Structural Similarity (SSIM) on the methods mentioned above.
Results
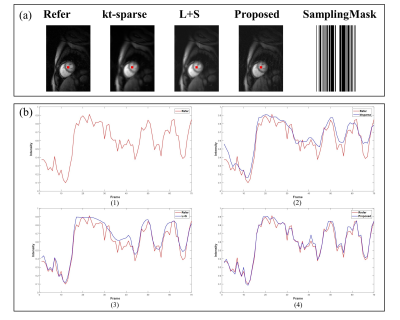
The proposed method had better reconstruction numerical results in different under-sampling ratios compare with other methods as shown in Table.1. Especially the numerical results are higher than those of other methods under the high reduction factor r=8 , which indicated that the proposed method had strong robustness. In the cardiac cine dataset, for reconstruction of the heart, the proposed method had low artifacts with Cartesian trajectory and r=2 as shown in FIG.2. There are also clearer reconstructions of the details of the heart as shown by the red arrows. In the time dimension, compared with the smooth transition of L+S method as shown in FIG.2. (c) , the proposed method can even retain more detail information. The above results show that the proposed method has good reconstruction results in time and space dimensions. In the cardiac perfusion dataset, the proposed method also had better reconstruction results than the other methods as shown in FIG.3.(a). Besides, we drew the ROI in myocardial regional and got the change curve in the time dimension shown in FIG.3. (b). We can clearly see that the proposed method is closer to the original signal strength value than the other methods, especially at the peak the proposed method had very close results. Finally, the proposed method has a fast convergence rate as shown in FIG.4. (a). The proposed method can reconstruct the image with higher quality after fewer iterations as shown in FIG.4. (b), which improves the problem of slow tensor reconstruction speed. All experiments clearly illustrate that the proposed method can get better reconstruction results in terms of both efficiency and effectiveness.Discussion and Conclusions
A novel tensor low-rank modeling reconstruction method was introduced for dMRI. The proposed method can make full use of the low-rank and sparse information of the tensor for reconstruction and explored the high and low frequency components of the frequency domain. Although not addressed here, the proposed method may also be applicable to other tensor based method. And its utility should be fully explored in future studies.Acknowledgements
NoneReferences
1. Lustig M , Santos J M , Donoho D L , et al. k-t SPARSE: High frame rate dynamic MRI exploiting spatio-temporal sparsity. Proc. 13th Annu. Meeting ISMRM.2006;pp. 2420.
2. Adluru G, Awate SP, Tasdizen T, Whitaker RT, Dibella EV. Temporally constrained reconstruction of dynamic cardiac perfusion MRI. Magn Reson Med. 2007;Jun 57(6):1027-36.
3. E. J. Candès, J. Romberg, and T. Tao, Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information.IEEE Trans. Inf. Theory.2006; vol. 52, no. 2, pp. 489–509, Feb.
4. M. Lustig, D. L. Donoho and J. M. Pauly, Sparse MRI: The application of compressed sensing for rapid MR imaging.Magn. Reson. Med.2010; vol. 58, no. 6, pp. 1182-1195.
5. Kim, et al. Accelerated phase-contrast cine MRI using k-t SPARSE-SENSE.Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine.2012.
6. Lingala S G. , Hu Y , Dibella E , et al. Accelerated Dynamic MRI Exploiting Sparsity and Low-Rank Structure: k-t SLR. IEEE Transactions on Medical Imaging,.2011;30(5):1042-1054,.
7. Otazo R , Candès, Emmanuel, Sodickson D K. Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine.2015; 73(3):1125-1136.
8. S. F. Roohi, D. Zonoobi, A. A. Kassim and J. L. Jaremko, Multi-dimensional low rank plus sparse decomposition for reconstruction of under-sampled dynamic MRI.Pattern Recognit.2017;vol. 63, pp. 667-679.
9. S. Ma, H. Du and W. Mei, Dynamic MR image reconstruction from highly undersampled (k t)-space data exploiting low tensor train rank and sparse prior. IEEE Access.2020; vol. 8, pp. 28690-28703.
10. D. Zhang, Y. Hu, J. Ye, X. Li and X. He, Matrix completion by truncated nuclear norm regularization. Comput. Vis. Pattern Recognit.2012; pp. 2192-2199.
11. Y. Wang and X. Su, Truncated nuclear norm minimization for image restoration based on iterative support detection.Math. Problems Eng.2014;no. 937560.
12. C. Lu, J. Feng, W. Liu, Z. Lin, S. Yan et al., Tensor robust principal component analysis with a new tensor nuclear norm. IEEE transactions on pattern analysis and machine intelligence.2019.
13. Chen, C. , et al. OCMR (v1.0)--Open-Access Dataset for Multi-Coil k-Space Data for Cardiovascular Magnetic Resonance Imaging .2020.
Figures