5127
Improved T1, T2 and PDFF mapping with rosette MRF using virtual-coil + low-rank + patch-based regularization1Department of Radiology, University of Michigan, Ann Arbor, MI, United States
Synopsis
Keywords: Heart, MR Fingerprinting
In this work, T1/T2/PDFF mapping with rosette cardiac MRF is improved by exploiting the idea of virtual coils along with subspace constrained reconstruction. The Hermitian symmetry of k-space is explicitly included in the forward model via virtual coils and combined with global low-rank models. This model is further combined with a regularizer leveraging prior information from dictionaries, patch-similarity, and locally low-rank. This virtual-coil + low-rank + patch-based approach is used to jointly reconstruct multi-echo rosette MRF data for improved quality of the final T1, T2, and PDFF maps.INTRODUCTION:
Global low-rank methods have been widely used in MR, for a variety of applications. In the context of MR Fingerprinting (MRF)1, global subspace constrained reconstructions2,3,4 help suppress residual aliasing commonly present in property maps derived from highly undersampled acquisitions. Partial Fourier5 reconstruction is another longstanding method that exploits the Hermitian symmetry of a (real) object for undersampled acquisitions, which has been studied under various formulations like PFPP,6 LORAKS,7 and Virtual Coil Concept.8 The first contribution in this work is combining virtual coils with global low-rank methods to leverage both types of a priori information.Regularization methods are also effective at suppressing aliasing and noise. Compressed Sensing,9 locally low-rank regularizers10 and dictionary based regularization,4,11 among others, have been proposed for MRF applications. Redundant information between similar image patches has been widely used in other fields (e.g. Non-Local-Means12, Block-Matching-3D13), and have also been investigated for MR in methods like LOST14 and (HD)-PROST15. The second contribution in this work is developing an MRF-tailored regularizer, incorporating ideas from,4,10,15 and combining it with the aforementioned virtual-coil + low-rank model. The proposed approach was evaluated for T1/T2/PDFF (Proton Density Fat Fraction) cardiac MRF in five healthy subjects.
METHODS:
A common way of incorporating low-rank constraints into the forward model is via the so-called Low-rank Inversion (LRI) expressed by the following problem:$$\boldsymbol{\hat{y}=argmin_y}\begin{Vmatrix}\boldsymbol{SU_{TR}Fy-s}\end{Vmatrix}_2^2,[eq.1]$$
where $$$\boldsymbol{S}$$$ is the sampling trajectory, $$$\boldsymbol{F}$$$ is the Fourier transform, $$$\boldsymbol{C}$$$ are coil sensitivities, $$$\boldsymbol{U_{TR}}$$$ is the low-rank subspace, $$$\boldsymbol{y}$$$ are the so-called singular images and $$$\boldsymbol{s}$$$ are the acquired data. In (single-echo) MRF, $$$\boldsymbol{U_{TR}}$$$ is commonly derived from the dictionary itself, used to compress the data along the TR dimension, and can be applied in k-space for computational advantages.
Virtual coils are a convenient way of leveraging Hermitian symmetry into the forward model, and may be exploited within a low-rank model via:
$$\boldsymbol{\hat{y}=argmin_y}\begin{Vmatrix}\boldsymbol{SU_{TR}F\begin{bmatrix}\boldsymbol{P}\\\boldsymbol{P*}\end{bmatrix}\begin{bmatrix}\boldsymbol{C}\\\boldsymbol{C*}\end{bmatrix}y-\begin{bmatrix}\boldsymbol{s}\\\boldsymbol{s'}\end{bmatrix}}\end{Vmatrix}_2^2,[eq.2]$$
where $$$\boldsymbol{P}$$$ is the image phase, and $$$\boldsymbol{s'(k)=s^*(-k)}$$$ (where $$$\boldsymbol{k}$$$ denotes k-space coordinate). For multi-echo data, we can further consider a low-rank compression $$$\boldsymbol{U_{TE}}$$$ along the echo-time dimension. Since eq. [2] reconstructs real-valued images, this basis could potentially be lower rank than for complex valued images; the corresponding model (also considering regularization) would be:
$$\boldsymbol{\hat{y}=argmin_y}\begin{Vmatrix}\boldsymbol{SU_{TR}F\begin{bmatrix}\boldsymbol{P}\\\boldsymbol{P*}\end{bmatrix}\begin{bmatrix}\boldsymbol{C}\\\boldsymbol{C*}\end{bmatrix}U_{TE}y-\begin{bmatrix}\boldsymbol{s}\\\boldsymbol{s'}\end{bmatrix}}\end{Vmatrix}_2^2+R(\boldsymbol{y}),[eq.3]$$
where $$$R$$$ is some regularizer. In practice, $$$\boldsymbol{U_{TE}}$$$ can be derived via a preliminary reconstruction from eq. [2]. The forward model in eq. [3], virtual-coil + low-rank (Fig.1-top), exploits Partial Fourier and redundant information along the TR and TE dimensions.
Additionally, we propose a novel regularizer, combining ideas from locally low-rank, geometric augmentation, patch-based and dictionary-based approaches, defined as:
$$R(\boldsymbol{y})= \sum_b \lambda_b\begin{Vmatrix}\boldsymbol{Q_bADD^Hy}\end{Vmatrix}_*,[eq.4]$$
where $$$\boldsymbol{D}$$$ is the MRF dictionary, $$$\boldsymbol{A}$$$ creates replicas of mirrored and rotated about the center, and $$$\boldsymbol{Q_b}$$$ finds a set of self-similar patches relative to pixel b and arranges them into a Casorati matrix. $$$\boldsymbol{DD^H}$$$ projects each fingerprint into its’ (compressed) dictionary entry of length Nr, producing a similar denoising effect to standard template matching used in MRF for parameter estimation. $$$\boldsymbol{A}$$$ creates eight copies of via basic (interpolation-less) mirror/rotation operations. This is relevant for the following step, as it creates additional redundant patches for self-similarity. Finally (and for each pixel b), $$$\boldsymbol{Q_b}$$$ finds a set of similar image blocks (of size NpxNp) via inner product, and arranges them into a Np2NrxNb (low-rank) matrix, which can be efficiently denoised via SVD. This patch-based regularizer (Fig.1-bottom) is combined with the virtual-coil + low-rank forward model, and applied to T1/T2/PDFF mapping in cardiac MRF.
EXPERIMENTS:
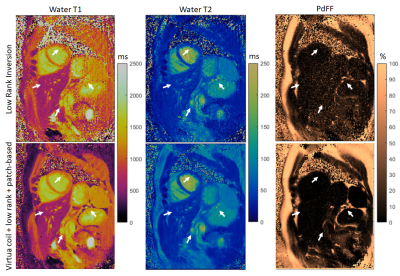
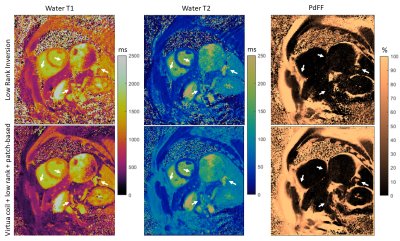
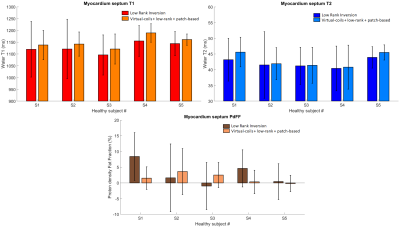
The proposed approach was evaluated in five healthy subjects (age = 31.0±13.1 years, 4 females) at 1.5T (Magnetom Sola, Siemens Healthineers, Erlangen, Germany) using an 18-channel cardiac coil. Imaging parameters included one short axis slice; field of view (FOV) = 300 mm2; 8 mm slice thickness; resolution = 1.56×1.56 mm2; TE/ΔTE/TR = 1.39/0.94/9.7 ms; flip angle = 4-25º; FISP readout; rosette trajectory; 15-heartbeat breath-hold. Data were reconstructed with LRI (eq. [1]) and with the proposed virtual-coil + low-rank + patch-based recon (eqs. [3,4]). Parametric values were measured in ROIs in the interventricular septum.RESULTS:
Residual aliasing and noise amplification are present in parametric maps reconstructed with LRI; however these artefacts are considerably reduced with the proposed approach (Fig.3, Fig.4). Additionally, a better delineation of structures, particularly around water/fat interfaces, was observed with the proposed approach. Mean T1 for the cohort was (in format [LRI; proposed]): [1127±23; 1150±25] ms, T2 was [42.0±1.5; 43.0±2.2] ms, PDFF was [2.8±3.8; 1.5±1.6] %. Corresponding standard deviations were [89±32; 48±16] ms, [6.8±2.6; 4.9±1.7] ms, [7.5±2.0; 4.2±1.8] %. T1/T2/PDFF values were in general agreement between LRI and virtual-coil + low-rank + patch-based, however a higher apparent precision (lower standard deviation) was observed for the latter (Fig.5). Slightly higher T1/T2 values were observed with the proposed method and are presumably due to the improved water/fat separation (and improved PDFF mapping with the proposed approach), which reduces bias from fat signal leaking into the water signal.CONCLUSION:
A novel forward model for multi-echo MRF is developed, combining virtual coils with global low-rank; furthermore a novel MRF denoiser is developed, combining ideas from dictionary-regularization, geometric image augmentation, patch-similarity and locally low-rank. The proposed approach outperformed conventional global low-rank and will be investigated further in comparison to gold standard methods.Acknowledgements
This work was supported by the NIH (R01 HL153034, R01HL163991) and Siemens healthcare.References
1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013 Mar;495(7440):187-92.McGivney DF, Pierre E, Ma D, et al. SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans. Med. Imaging 2014;33:2311–2322 doi: 10.1109/TMI.2014.2337321.
2. McGivney DF, Pierre E, Ma D, et al. SVD compression for magnetic resonance fingerprinting in the time domain. IEEE Trans. Med. Imaging 2014;33:2311–2322 doi: 10.1109/TMI.2014.2337321.
3. Zhao B, Setsompop K, Adalsteinsson E, et al. Improved magnetic resonance fingerprinting reconstruction with low-rank and subspace modeling. Magn. Reson. Med. 2018;79:933–942 doi: 10.1002/mrm.26701.
4. Assländer J, Cloos MA, Knoll F, Sodickson DK, Hennig J, Lattanzi R. Low-rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med. 2018;79:83–96 doi: 10.1002/mrm.26639
5. Noll DC, Nishimura DG, Macovski A. Homodyne detection in magnetic resonance imaging. IEEE transactions on medical imaging. 1991 Jun;10(2):154-63.
6. Bydder M, Robson MD. Partial Fourier partially parallel imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2005 Jun;53(6):1393-401.
7. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE transactions on medical imaging. 2013 Dec 5;33(3):668-81.
8. Blaimer M, Gutberlet M, Kellman P, Breuer FA, Köstler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2009 Jan;61(1):93-102.
9. Davies M, Puy G, Vandergheynst P, Wiaux Y. A compressed sensing framework for magnetic resonance fingerprinting. Siam journal on imaging sciences. 2014;7(4):2623-56.
10. Lima da Cruz G, Bustin A, Jaubert O, Schneider T, Botnar RM, Prieto C. Sparsity and locally low-rank regularization for MR fingerprinting. Magnetic resonance in medicine. 2019 Jun;81(6):3530-43.
11. Cline CC, Chen X, Mailhe B, Wang Q, Pfeuffer J, Nittka M, Griswold MA, Speier P, Nadar MS. AIR-MRF: accelerated iterative reconstruction for magnetic resonance fingerprinting. Magnetic resonance imaging. 2017 Sep 1;41:29-40.
12. Coupé P, Yger P, Prima S, Hellier P, Kervrann C, Barillot C. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE transactions on medical imaging. 2008 Mar 31;27(4):425-41.
13. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising with block-matching and 3D filtering. InImage processing: algorithms and systems, neural networks, and machine learning 2006 Feb 17 (Vol. 6064, pp. 354-365). SPIE.
14. Akçakaya M, Basha TA, Goddu B, Goepfert LA, Kissinger KV, Tarokh V, Manning WJ, Nezafat R. Low‐dimensional‐structure self‐learning and thresholding: regularization beyond compressed sensing for MRI reconstruction. Magnetic Resonance in Medicine. 2011 Sep;66(3):756-67.
15. Bustin A, Lima da Cruz G, Jaubert O, Lopez K, Botnar RM, Prieto C. High‐dimensionality undersampled patch‐based reconstruction (HD‐PROST) for accelerated multi‐contrast MRI. Magnetic resonance in medicine. 2019 Jun;81(6):3705-19.
Figures
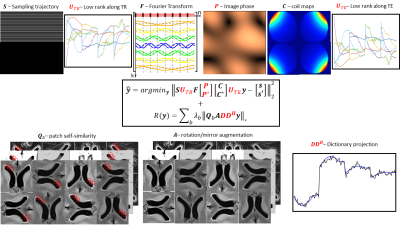
Diagram of the proposed virtual-coil + low-rank + patch-based reconstruction.
The forward model (top) incorporates phase information to exploit the Hermitian symmetry of k-space. Low-rank subspaces, UTR and UTE, are employed to exploit redundant temporal information along the TR and TE dimensions, respectively.
The proposed patch-based regularizer incorporates a priori information from the MRF dictionary D, followed by geometric augmentation before assessing self-similarity. Each set of similar blocks are reshaped into Casorati matrices and jointly denoised via SVD.
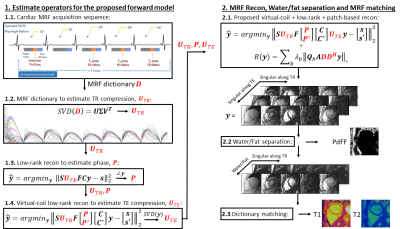
Proposed MRF framework for cardiac T1/T2/PDFF.
1.1 Data is acquired with a rosette cardiac MRF sequence.
1.2 Temporal compression along TR is derived from the MRF dictionary.
1.3 A preliminary low-rank reconstruction is used to estimate the image phase.
1.4 Another preliminary reconstruction is used to estimate the compression along the TE.
2.1 The estimated UTR, P and UTE are incorporated into the proposed reconstruction (Fig.1).
2.2 The reconstructed MRF series is water/fat separated, yielding PDFF.
2.3 The water images are used for MRF dictionary matching, yielding T1/T2.