Introduction

After adjusting transmit gain for a target location, RF coil sensitivity is determined by local receive B₁. For surface coils, the highly inhomogeneous transmit and receive B₁ must be separated to accurately characterize performance of different coil geometries. Normalizing the local excitation separately for each position (eg. to local 90°, with TR>>T₁ for peak signal in each voxel) at sufficient detail would require many measurements. Instead, the signal vs. transmit power curve can be sampled, without need for multiple localized power adjustments, and fit to image voxel signals to estimate the local peak SNRs.

Methods

The SNR geometry of two cryogenically cooled RF coils were assessed using gradient-recalled echo imaging (FLASH) of a 50ml phantom containing 2M ¹³C-Urea and 2mM DOTAREM™ (T₁=860ms, T₂=90ms).

Imaging System:
A 7T preclinical scanner (Agilent/GE/Bruker) with two CryoProbe^TM (Bruker) transmit-receive ¹³C RF coils, both featuring cryogenically cooling of the 20mm diameter coil elements (30K) and preamplifier (77K) with gaseous helium. One coil had a linear coil configuration (lcryo), and one quadrature with two partially-overlapping coil elements (qcryo). Both Cryocoils were used in combination with a ¹H 86mm volume resonator (Bruker). In addition, a ¹³C/¹H dual-tuned volume resonator (31mm ID, Rapid Biomedical) at room temperature was used.

MR Measurement:
Imaging parameters for the FLASH were FOV 32x32mm², matrix 64x64, slice thickness 3mm centered axially with the coil elements, TR 4000ms, TE 4.34ms, Shinnar-Le Roux (SLR) pulse, nominal 90° tip angle, 2ms pulse duration and 4kHz pulse bandwidth, 9 repetitions each. The measurement was repeated with 21 different RF powers to compensate for the inhomogeneous excitation profiles. One image was acquired with nominal 0 RF power for noise determination.
To consider the inhomogeneous excitation profile of the surface coils, a B₁ transmit/receive map was generated by performing a per-voxel fit to the signal S:

$$S(RF_{power}) = A* sin(π/p \times \sqrt(RF_{power}))$$

With A $$$\in$$$ ℂ. A 90° tip angle is reached with $$$RF_{power} = \frac{p^2}{4}$$$, and local peak signal given by |A|.
Maps of reference power were also calculated, which indicate the local RF pulse power calibration.

Signal to noise ratio:
The noise was obtained by fitting a Rayleigh distribution to the histogram of the voxels of the image acquired with nominal zero RF power and taking the standard deviation ($$$\sigma$$$) as noise [1].
The SNR for each image voxel was then calculated as:

$$ SNR = |A| / \sigma$$

Bloch Simulations:
A 2ms 4kHz SLR pulse in combination with a gradient of 14.564 kHz/cm (3mm slice thickness) with different B₁-amplitudes was simulated to estimate slice excitation profiles [2].

Results

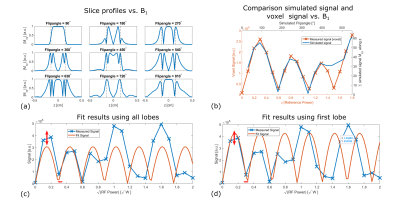
Bloch simulations:
The slice profiles degrade with increasing B₁. A nominal 180° tip angle only inverts the magnetization at the center of the slice (fig. 2 (a)).

B₁ Mapping:
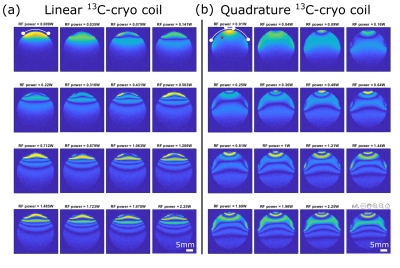
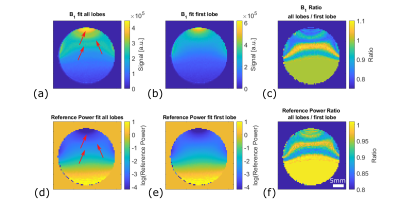
With increasing RF power, bands of excited and inverted magnetization become visible (fig. 1). Fitting a sinusoidal against the complex signal becomes inaccurate, especially for voxels close to the coil surface. This can be explained with the Bloch simulations that show a degradation of slice profile with increasing B₁ (fig.2 (a,b)). Using only the signal up to the first inversion, where the assumption of a sinusoidal signal behavior is still valid, fits the signal better (fig2 c,d) and leads to smoother B₁ receive maps (fig3 a,b), higher estimated receive B₁ (fig3.c) as well as smoother and higher reference power maps (fig3 c-e).

Signal to noise ratio:
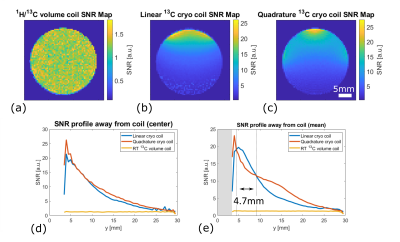
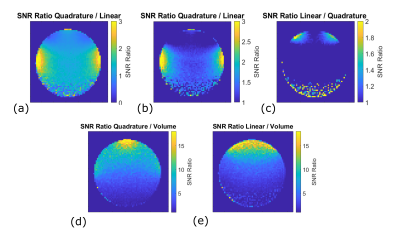
Highest SNR is measured near the overlapping coil elements (c) of the qcryo. Otherwise, the lcryo has better SNR until 4.7mm away from the coil surfaces, after which the qcryo has higher SNR. The lcryo has higher SNR (>2x) compared to the qcryo close to its coil elements. The qcryo has higher SNR (>3x) compared to the lcryo close to its non-overlapping elements and in the region more than 5 mm away from coil surface (SNR ~1.1 -2). A comparison of the SNR maps shows overall better performance of cryocoils compated to the room-temperature volume coil (fig.5).

Discussion

RF coils have highest peak SNR when the object is close to the coil elements due to near-field effects. The localized high near-coil SNR of the qcryo at the center and sides occurs due to the coil element wires, as seen in Fig. 1.
Degrading slice profiles must be addressed when fitting the receive B₁. Alternate solutions could include different RF pulse shapes to correct the profiles at higher tip angles, or employing 3D readout to reduce the impact of averaging across slice profiles, at the cost of increased acquisition time for additional phase encodes.
Due to its better SNR performance close-in, the lcryo could be used in subcutaneous mouse tumor models, whereas the qcryo, due to its higher penetration depth, could be more useful in abdominal organs or tumor models. With pulse sequences that benefit from homogeneous transmit B₁, such as bSSFP, the volume resonator could be of advantage.

Conclusions

Both linear and quadrature cryo coils have high SNR performance compared to a room-temperature volume coil. The linear cryocoil outperforms the quadrature up to ~5mm away from the coil, while the quadrature cryocoil has higher penetration depth and higher SNR at the edges of the coil.

References

[1] Gudbjartsson, Hákon, and Samuel Patz. "The Rician distribution of noisy MRI data." Magnetic resonance in medicine 34.6 (1995): 910-914.

[2] Hargreaves B, Bloch Equation Simulator. http://mrsrl.stanford.edu/~brian/blochsim/ Accessed November 9, 2021.