Synopsis

Keywords: Machine Learning/Artificial Intelligence, Diffusion/other diffusion imaging techniques, Model fitting, uncertainty, IVIM

Uncertainty is an important aspect of fitting quantitative models to diffusion MRI data, which is often overlooked. This study presents a method for estimating uncertainty intrinsic to a model using a generative deep learning approach (Denoising Diffusion Probabilistic Models (DDPM)). We numerically validate that the approach provides accurate uncertainty estimates, and demonstrate its use in providing signal-specific uncertainty estimates. Furthermore, we show that DDPM can be used as a fitting method that estimates uncertainty, and show both ADC and IVIM fitting on an in vivo brain scan. This shows promise for DDPM, as both an investigate tool and fitting method.

Purpose

Quantitative model fitting is a common procedure in diffusion MRI¹. Quantitative parameters can be reproduced across scanners and institutions² and therefore could form a reliable basis for detecting pathology.

Uncertainty is often overlooked in model fitting. Ignoring uncertainty carries the risk of misinterpreting fitted parameters. Whereas uncertainty leads to noise amplification in conventional fitting, supervised deep learning models exhibit bias as uncertainty increases. Bootstrap methods^3-5 are a common approach to assessing uncertainty during fitting. These methods rely on repeated fitting and can be slow, and biased by the fitting method itself.

Here, we propose a method for estimating the intrinsic uncertainty of model fitting, based on a Denoising Diffusion Probabilistic Model (DDPM)⁶, a state-of-the-art generative deep learning model popular in image generation^7,8. Our method is agnostic to the fitting method, and instead assesses the intrinsic uncertainty of the model function. Furthermore, DDPM can be applied as a fitting method.

In this study, we demonstrate our DDPM model on fitting a mono-exponential diffusion model and an intravoxel incoherent motion (IVIM) model⁹, on both synthetic data and an in vivo scan. We validated DDPM uncertainty estimates using a numerical approach.

Methods

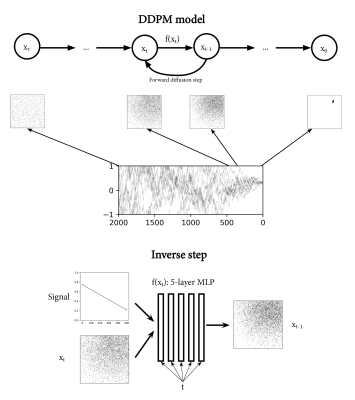
DDPM model
The DDPM model is trained to draw random samples from a conditional probability density function (pdf) $$$f(p|s)$$$ (probability of parameters $$$p$$$, given signal $$$s$$$), illustrated in Figure 1. It was trained with synthetic data generated from the model function ($$$s=M(p)+noise$$$). Training was run for 1000 epochs of 500 batches with batch size 128, and took ~9.5 hours per model on a single CPU core.

DDPM inference was accelerated by a factor ten¹⁰. For inference on single signals, we drew 10000 samples using the DDPM model, taking 3s on a RTX A6000 GPU. For inference on $$$246\times246$$$ images, we drew 100 samples per pixel, taking 10s per sample.

Numerical validation
To numerically approximate a sample from the pdf $$$f(p|s)$$$, we simulated a large quantity of $$$(p,s)$$$ pairs. For a given signal, we find the nearest neighbours in signal-space among these simulations, where the associated parameters ($$$p$$$) approximate a sample from the pdf.

Experiments
We applied DDPM to diffusion MRI fitting of a trace ADC signal ($$$b=[0,500]$$$) and an IVIM signal with 16 b-values¹¹. Signals with Rician noise ($$$\text{SNR}=100$$$ for $$$S_0=1$$$) were generated for ADC:
$$s_{\{xx,yy,zz\}}=S_{0}\cdot~exp(-b\cdot~D_{\{xx,yy,zz\}})$$
And IVIM:
$$s_{\{xx,yy,zz\}}=S_0\cdot~((1-f)\cdot~exp(-b\cdot~D_{\{xx,yy,zz\}})+f\cdot~exp(-b\cdot~D^*)$$
$$$S_0$$$ was sampled in the range $$$[0,1]$$$, $$$D_{\{xx,yy,zz\}}$$$ in $$$[0,\text{3e-3}]$$$, $$$f$$$ in $$$[0,0.5]$$$, and $$$D^*$$$ in $$$[\text{3e-3},\text{100e-3}]$$$. For b-values except 0 the trace signal was calculated. The training targets were the simulated parameters and $$$ADC=(D_{xx}+D_{yy}+D_{zz})/3$$$, instead of $$$D_{\{xx,yy,zz\}}$$$.

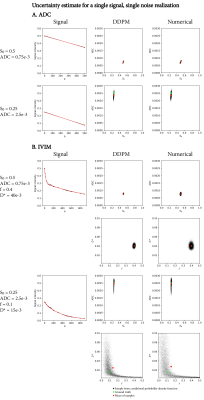
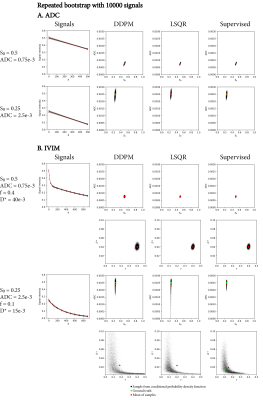
For comparison, we performed non-linear least squares (LSQR) fitting and fitting with a supervised neural network. We estimated uncertainty for signals with a single noise realization, with 10000 random noise realizations (i.e. a repeated bootstrap), and fitting of a brain scan of a volunteer (acquired in accordance with institutional guidelines).

Results

Figure 2 shows the estimated uncertainty for two specific signals per model. The uncertainty estimates from DDPM and the numerical method matched closely, with DDPM showing a minor bias towards more probable regions.

Figure 3 shows the uncertainty as estimated by a repeated bootstrap. DDPM yielded the broadest distribution of samples, consistent with Figure 2, whereas LSQR and supervised fitting showed some bias.

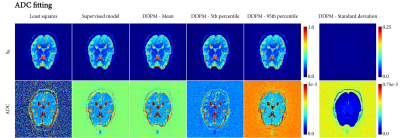
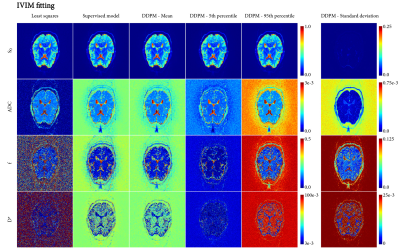
Figures 4 and 5 show fitting on an in vivo image of the brain. The ADC fitting showed little uncertainty, with minor differences among the methods. In IVIM, however, DDPM uncovered substantial uncertainty in the $$$f$$$ and $$$D^*$$$ maps.

Discussion

We demonstrated that DDPM provides accurate uncertainty estimates with respect to a numerical simulation in both ADC and IVIM fitting, and that it can visualize and assess uncertainty for specific signals. The DDPM uncertainty estimate is specific for the observed noise of a single signal, requires no additional samples like a bootstrapping approach would, and is not dependent on a specific fitting method.

In IVIM, using DDPM either as an investigative tool (Figures 2 and 3), or as a fitting method (Figure 5), showed that uncertainty in $$$f$$$ and $$$D^*$$$ is correlated, and that the $$$D^*$$$ estimate was unreliable in most parts of the brain.

DDPM could investigate far more non-linear behaviour than shown, limited primarily by the training data. Synthetic data can be manipulated to investigate expected changes in uncertainty, e.g. using variable SNR, or introducing spatial correlations. Real data can also be used for training.

A main limitation of our proposed method is training time. While our implementation was not optimized for speed, it is unlikely to become fast enough to allow iterative investigations, e.g. optimizing acquisition parameters. Furthermore, sampling using DDPM models is relatively slow, drawing a single sample takes 100 times longer than using a conventional neural network, which needs to be repeated to accurately estimate uncertainty.

Especially when fitting with DDPM, this repeated sampling presents an interesting visualization problem. Many random samples per pixel need to be condensed into a few images, which may not capture the complexity of the underlying uncertainty.

The DDPM approach presents a novel method of assessing uncertainty in highly non-linear models. In quantitative MRI, and diffusion MRI in particular, this provides a valuable investigative tool in model fitting and experimental design.

Acknowledgements

This work was supported by the Research Council of Norway (FRIPRO Researcher Project 302624).