5022

Toolkit for capillary pseudo-diffusivity Monte Carlo simulations
Elizabeth Powell1, Geoff JM Parker1,2,3, and Marco Palombo4,5
1Centre for Medical Image Computing, Medical Physics and Biomedical Engineering, University College London, London, United Kingdom, 2Queen Square MS Centre, Institute of Neurology, University College London, London, United Kingdom, 3Bioxydyn Limited, Manchester, United Kingdom, 4Cardiff University Brain Research Imaging Centre, School of Psychology, Cardiff University, Cardiff, United Kingdom, 5School of Computer Science and Informatics, Cardiff University, Cardiff, United Kingdom

Synopsis

Keywords: Diffusion/other diffusion imaging techniques, Simulations, Pseudo-diffusivity

The pseudo-diffusivity effect - arising from blood flow in capillaries - is used to characterise the diffusion-weighted MRI signal at low b-values (b<200 s/mm2) in several biophysical models. We propose here a generative model for producing vascular meshes with tunable properties - such as vessel segment radius and length, and vessel volume fraction – that are compatible with common Monte Carlo diffusion simulation frameworks. Monte Carlo simulations of pseudo-diffusivity are performed, under varying conditions, by adapting the Camino simulation toolkit to include a plug flow component to spin dynamics inside the vascular mesh; the resulting signals are validated against analytical solutions.

Introduction

Several biophysical models - such as the IVIM1,2, VERDICT3, and, more recently, blood-brain barrier water exchange4,5 models - exploit the pseudo-diffusivity effect arising from blood flow in the vasculature to characterize the diffusion-weighted MRI signal at low b values (b<200 s/mm2). However, to our knowledge, there are no currently available methods for generating numerical phantoms that accurately reflect vascular properties - such as vessel segment radius, segment length, orientation distributions, and vessel volume fraction – and that are compatible with common Monte Carlo diffusion simulation frameworks6-8. Here we propose a generative model of vascular meshes for Monte Carlo simulations of flow dynamics in capillary vasculature, implemented using the Camino toolkit6. We use the toolkit to simulate the effects of plug flow on the diffusion signal under a range of conditions.

Methods

Generative vascular mesh model
Our graph theory-based generative model uses a set of nodes defined on a grid spanning a user-defined substrate size, L. Edges are added between nodes using a 6-node neighbourhood. A continuous, non-intersecting, random path through the substrate is then generated from an initial seed node by iteratively stepping to a connected node until the initial node is returned to. The path is then subsampled to provide a final vessel skeleton with the desired distribution of segment lengths and orientations. The resulting skeleton is converted into a 3D surface mesh with a user-defined segment radius.

Monte Carlo methods
We extend here the Camino6 framework for Monte Carlo diffusion simulations to model flow as a drift with uniform velocity distribution across the vessel segments. Specifically, for blood flowing with velocity, vb, intravascular spins drift a distance δxb = vbδt along a vessel segment in one timestep, δt.

Validation
To validate our framework (generative model and Monte Carlo simulations), we compared our simulation results with theoretical predictions. In the ballistic regime, where spins do not change direction during the diffusion time, the signal arising exclusively from flow can be described as S = S0 sinc(4πqΔvb)9, where q is the dephasing parameter and Δ the diffusion time, if capillary segments are randomly oriented. A Monte Carlo simulation of ballistic flow was performed using ~106 spins, Δ = 0.5 ms, gradient duration δ ~ 0 ms and three flow velocities vb = [1.5, 2.0, 2.5] mm/s. Phase accumulation was computed using the short gradient pulse (SGP) approximation. Signal-vs-b curves were generated for 100 b-values between b = 0-1000 s/mm2 each with 32 directions and compared against the analytical solution.

We also performed simulations in the IVIM regime, where spins are assumed to change direction >5 times during the diffusion time. The signal arising exclusively from flow (if capillary segments are randomly oriented) can be described as S = S0 exp(-bD*), where the pseudo-diffusivity is D* = lvb / 6 and l is the vessel segment length. Monte Carlo simulations of diffusive flow were performed using Δ = 100 ms, δ = 20 ms and three flow velocities vb = [1.5, 2.0, 2.5] mm/s. Phase accumulation was computed using the Gaussian phase approximation (GPA). Signal-vs-b curves were generated for 100 b-values between b = 0-250 s/mm2 with 32 directions and compared against the analytical solution.

Results

A vascular mesh was generated (Figure 1) with ~2000 individual segments, a mean vessel length of 25 µm and vessel radius of 4 µm, giving a vascular density of 4 % in a substrate with size 300 × 300 × 300 µm3. Plug flow was successfully simulated along the length of the simulated capillary bed, which conformed to critical characteristics required for the IVIM model to be valid: the expected diffusion distance as a function of diffusion time agreed with the analytical solution (Figure 2A), and the angular distribution of the segments was approximately uniform (to within numerical errors) (Figure 2B). Figure 2C also shows that the mean segment length agrees with literature values10, with an approximately Gaussian spread.

Figure 3 validates our framework further, demonstrating good agreement between simulations and analytical solutions for attenuation down to one order of magnitude for both the ballistic and IVIM regimes, demonstrated at three simulated blood velocities.

Discussion

Our simulated vascular mesh demonstrates good correspondence with literature values for characteristics such as vessel segment length, orientation distribution10, and vascular volume fraction11-13. Our initial, relatively simple, simulated vessel structure allows effective Monte Carlo simulation of capillary flow; our next step is to incorporate a distribution of radii and to enable vessel branching, allowing arbitrary capillary geometries to be modelled.

The Monte Carlo simulations demonstrated good correspondence with analytical solutions, indicating successful implementation of plug flow spin dynamics within the Camino framework.

Conclusions

We present a novel approach to generating vascular meshes using graph theory and random walk processes. While further validation of the resulting meshes is required, we demonstrate that the algorithm has good potential for creating vascular structures with tunable parameters including vascular density, mean segment length and segment diameter, and surface permeability (i.e. exchange).

Acknowledgements

This work was supported by EPSRC grants EP/S031510/1 and EP/M005909/1. MP is supported by UKRI Future Leaders Fellowship MR/T020296/2.

References

  1. D Le Bihan, E Breton, D Lallemand, P Grenier, E Cabanis, and M Laval-Jeantet. “MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders.” In: Radiology 161.2 (1986), pp. 401–407. doi: 10.1148/radiology.161.2.3763909.
  2. D Le Bihan, E Breton, D Lallemand, M L Aubin, J Vignaud, and M Laval-Jeantet. “Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging.” In: Radiology 168.2 (1988), pp. 497–505. doi: 10.1148/radiology.168.2.3393671.
  3. E Panagiotaki, S Walker-Samuel, B Siow, S P Johnson, V Rajkumar, R B Pedley, M F Lythgoe, and D C Alexander. “Noninvasive quantification of solid tumor microstructure using VERDICT MRI”. In: Cancer Research 74.7 (2014), pp. 1902–1912. doi: 10.1158/0008-5472.CAN-13-2511.
  4. R Bai, Z Li, C Sun, Y Hsu, H Liang, and P Basser.“Feasibility of filter-exchange imaging (FEXI) in measuring different exchange processes in human brain”. In: NeuroImage 219 (2020), p. 117039. doi: 10.1016/j.neuroimage.2020.117039.
  5. E Powell, Y Ohene, M Battiston, L M Parkes, and G J M Parker. “Voxel-wise compartmental modelling of blood-brain barrier water exchange measurements using FEXI”. In: In Proceedings of the 30th Annual Meeting of ISMRM, London,UK (2022)
  6. M G Hall and D C Alexander. “Convergence and Parameter Choice for Monte-Carlo Simulations of Diffusion MRI”. In: IEEE Transactions on Medical Imaging 28.9(2009), pp. 1354–1364. doi: 10.1109/TMI.2009.2015756.
  7. H H Lee, E Fieremans, and D S Novikov. “Realistic Microstructure Simulator (RMS): Monte Carlo simulations of diffusion in three-dimensional cell segmentations of microscopy images”. In: Journal of Neuroscience Methods 350. August 2020 (2021), p. 109018.doi: 10.1016/j.jneumeth.2020.109018.
  8. J R Li, V D Nguyen, T N Tran, J Valdman, C B Trang, K Van Nguyen, D T S Vu, H A Tran, H T A Tran, and T M P Nguyen. “SpinDoctor: A MATLAB toolbox for diffusion MRI simulation”. In: NeuroImage 202. January (2019), p. 116120. doi: 10.1016/j.neuroimage.2019.116120.
  9. W S Price. NMR Studies of Translational Motion. Cambridge: Cambridge University Press, 2009. doi: 10.1017/CBO9780511770487.
  10. L A Scott, B R Dickie, S D Rawson, G Coutts, T L Burnett, S M Allan, G J M Parker, and L M Parkes. “Characterisation of microvessel blood velocity and segment length in the brain using multi-diffusion-time diffusion-weighted MRI”. In: Journal of Cerebral Blood Flow and Metabolism (2020). doi: 10.1177/0271678X20978523.
  11. T Yamaguchi, I Kanno, K Uemura, F Shishido, A Inugami, T Ogawa, M Murakami, and K Suzuki. “Reduction in regional cerebralmetabolic rate of oxygen during human aging”. In: Stroke 17.6 (1986), pp. 1220–1228. doi:10.1161/01.STR.17.6.1220.
  12. K L Leenders et al. “Cerebral blood flow, blood volume and oxygen utilization: Normal values and effect of age”. In: Brain 113.1 (1990), pp. 27–47. doi: 10.1093/brain/113.1.27.
  13. J Hatazawa et al. “Regional cerebral blood flow, blood volume, oxygen extraction fraction, and oxygen utilization rate in normal volunteers measured by the autoradiographic technique and the single breath inhalation method”. In: Annals of Nuclear Medicine 9.1(1995), pp. 15–21. issn: 09147187. doi: 10.1007/BF03165003.

Figures

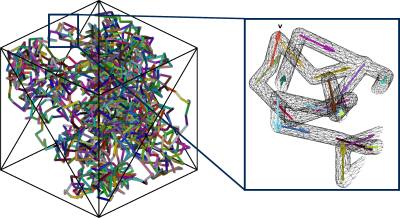
Figure 1. Vascular mesh. Left: The full vascular mesh is shown, inside a "voxel" substrate with dimensions 300 × 300 × 300 µm3. Right: A magnified section is displayed, highlighting the flow vectors that are defined for each vessel segment.

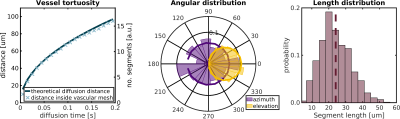
Figure 2. Vascular mesh characteristics. Left: The theoretical diffusion distance a spin with pseudo-diffusivity D* = lv / 6 would travel is plotted as a function of diffusion time (dark blue line) along with the distance a spin with velocity vb travelled inside the mesh during a Monte Carlo simulation of the same diffusion time (light blue markers). Centre: Angular distribution of vessel segments in the mesh (wedges) and of a true uniform distribution over the sphere (lines). Right: Length distribution of vessel segments in the mesh; the dashed line indicates the distribution mean.

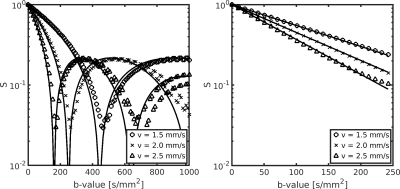
Figure 3. Monte Carlo simulations of flow inside the vascular mesh. Left: Signal-vs-b curves for Monte Carlo simulations in the ballistic regime (markers) and analytical solutions (solid lines). Right: Signal-vs-b curves for Monte Carlo simulations in the IVIM regime (markers) and analytical solutions (solid lines).

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
5022
DOI: https://doi.org/10.58530/2023/5022