5020
Estimating transcytolemmal water exchange from the Kärger model using a Bayesian method in a rat model of ischemic stroke1Key Laboratory for Biomedical Engineering of Ministry of Education, Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hanzhou, China, 2Department of Medical Imaging, Weifang Medical University, Shandong, China
Synopsis
Keywords: Diffusion/other diffusion imaging techniques, Brain
Transcytolemal water exchange can be estimated using diffusion-time-dependent diffusion kurtosis imaging acquired at long diffusion times. However, dMRI signals acquired at long diffusion times using STEAM sequences are typically noisy, and fitting of the nonlinear kurtosis model and the Kärger model accumulates fitting errors. Here, we proposed a Bayesian method for estimating transcytolemal exchange time from the Kärger model and compared accuracy and robustness with conventional least square fitting method in both simulated data and rat brain data in a model of transient middle cerebral artery occlusion. Results indicated improved fitting accuracy and robustness against noise using the Bayesian approach.Introduction
Recently, diffusion-time (td) dependent diffusion kurtosis imaging (tDKI) [1; 2] using stimulated echo acquisition mode (STEAM)-DWI pulse sequences [3; 4] has been proposed to probe transcytolemmal water exchange, e.g., using the Kärger model (KM) [5-7]. Some simulation and preclinical studies [1; 2; 8; 9] have demonstrated its potential in quantifying exchange time in grey matter and cancers. However, since data acquired with STEAM sequences have low SNRs (signal is half of the pulse gradient spin-echo sequence), fitting of the nonlinear kurtosis model and the KM accumulates fitting errors. The accuracy and robustness of tDKI data fitting with high noise have not been investigated. This study proposed using the Bayesian probability theory for the analysis of tDKI data and compared its performance with the nonlinear least squares (NLLS) method in both simulated data and rat brain data in a model of transient middle cerebral artery occlusion (MCAO).Methods
Simulation data: Simulation data were generated using Matlab with instantons kurtosis at infinitely short td (K0)=1.5, 1.8, 2.1, and 2.4, and transcytolemmal exchange time (tex)=10, 20, 50, and 80ms. Gaussian noise was added to the signal to achieve SNR=10 and 20.Data acquisition: Two rats underwent the MCAO model by occlusion of the middle cerebral artery to induce transient ischemia, followed by reperfusion after 2 hours[10]. MRI scans were performed before occlusion and at 2h, 6h, 12h, 24h, and 72h after reperfusion on a 7.0T Bruker scanner using a rat brain array surface coil. The diffusion-weighted STEAM sequence was performed at six td (20, 50, 80, 100, 150, and 200ms) with one b0, three b-shells (b = 800, 1500, 2500 s/mm2), and 18 diffusion directions. Coronal slices with 1mm-thickness were acquired with TE = 18ms, TR = 2000ms, FOV = 24×19.2mm2, matrix size = 80×64, yielding in-plane resolution = 0.3×0.3 mm2.
Data analysis: dMRI data were fitted using the DKE toolbox [11] to obtain diffusivity and kurtosis maps at individual td, which were fed into the KM for estimating K0 and tex while fixing K∞=0:
$$S(t,b)=S_0 (t) exp(-bD+1/6 b^2 D^2 K(t))$$
$$K(t)=K_0 (2t_ex)/t[1-t_ex/t(1-e^(-t/t_ex ))]+K_∞$$
NLLS curve fitting was performed in MATLAB, which was repeated 100 times with randomized initialization. A house-made Bayesian fitting pipeline was developed according to Gustafsson et al [12] with lognormal and reciprocal priors, and we took the mean, median, and mode as a central tendency measure of the K0 and tex estimation. The two methods were compared based on the accuracy as evaluated by mean square error (MSE) and robustness as evaluated by the standard deviation (STD).
Results
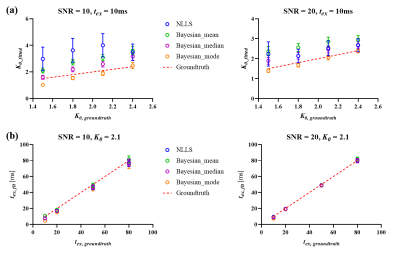
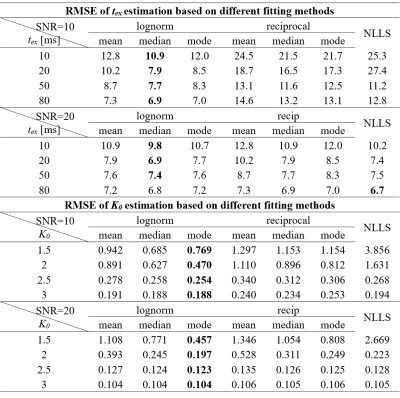
Simulation experimentFigure 1a showed correlation of estimated K0 with groundtruth based on NLLS analysis and Bayesian methods. All Bayesian outputs dramatically decreased the STD than NLLS at all SNR levels (Figure 1a), and the Bayesian results using lognormal prior and the mode as a central tendency measure had the lowest average RMSE, as shown in Table 1. As for tex estimation, the Bayesian results using lognormal prior and the median as a central tendency measure resulted in the lowest average RMSE compared to NLLS as shown in Table 1, while the two methods gave similar STD at all SNR levels (Figure 1b).
Animal experiments
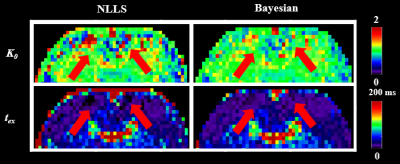
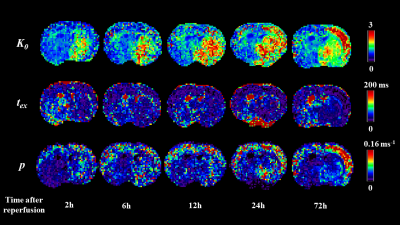
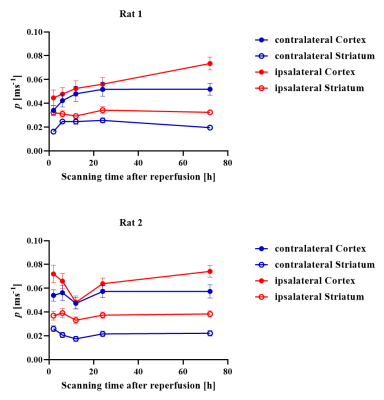
Figure 2 shows the estimated K0 and tex maps in a normal rat brain NLLS and Bayesian methods. Some voxels (red arrows) reached the fitting boundary and there were more outliers in the NLLS fitting compared with the Bayesian fitting. The measured tex = 24.0±16.3 ms in the normal cortex is consistent with previous reports for the in vivo rat brain [8]. Figure 3 shows a representative rat scanned longitudinally at 2-72h after reperfusion, which revealed the increase of cell membrane permeability following MCAO, as evaluated by permeability p (the reciprocal of tex). p increased instantly in the ipsilateral striatum at 2hrs after injury, and the ipsilateral cortex showed elevated p around 24 hours after injury. Figure 4 quantified the time course of p during the progression of injury, which increased continuously in the ipsilateral cortex between 2- 72h, while in the ipsilateral striatum, p first increased between 2- 24h, and fell back at 72h.
Discussion and Conclusion
This study demonstrated that compared with the least squares method, the Bayesian fitting achieved higher robustness while ensuring accuracy. Moreover, using the median for tex estimation while the mode for K0 estimation as a central tendency measure provided better performance for the lognormal prior. We also demonstrated the feasibility of measuring the transcytolemmal water exchange rate with tDKI in a rat model of ischemic injury. The longitudinal change of transcytolemmal permeability revealed a distinct pattern of injury progression after ischemia insult. Statistical analysis with a larger sample size and comparison with histology for the transcytolemmal permeability will be performed in future experiments.Acknowledgements
This work was supported by the Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600), the National Natural Science Foundation of China (61801424, 81971606, 82122032, 2021ZD0200202), and the Science and Technology Department of Zhejiang Province (202006140, 2022C03057).References
1. Zhang J, Lemberskiy G, Moy L, Fieremans E, Novikov DS, Kim SG (2021) Measurement of cellular-interstitial water exchange time in tumors based on diffusion-time-dependent diffusional kurtosis imaging. NMR in Biomedicine 34:e4496
2. Fieremans E, Novikov DS, Jensen JH, Helpern JA (2010) Monte Carlo study of a two-compartment exchange model of diffusion. NMR in Biomedicine 23:711-724
3. Kleinnijenhuis M, Mollink J, Lam W et al (2017) Choice of reference measurements affects quantification of long diffusion time behaviour using stimulated echoes. Magnetic Resonance in Medicine 79
4. Merboldt KD, Hänicke W, Frahm J (1991) Diffusion Imaging Using Stimulated Echoes. Magnetic Resonance in Medicine 19:233-239
5. KÄRger J, Pfeifer H, Heink W (1988) Principles and Application of Self-Diffusion Measurements by Nuclear Magnetic Resonance. In: Waugh JS, (ed) Advances in Magnetic and Optical Resonance. Academic Press, pp 1-89
6. Kärger J (1985) NMR self-diffusion studies in heterogeneous systems. Advances in Colloid and Interface Science 23:129-148
7. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K (2005) Diffusional kurtosis imaging: The quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine 53:1432-1440
8. Jelescu IO, de Skowronski A, Geffroy F, Palombo M, Novikov DS (2022) Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange. NEUROIMAGE 256:119277
9. Solomon E, Lemberskiy G, Baete S et al (2022) Time-dependent diffusivity and kurtosis in phantoms and patients with head and neck cancer. Magnetic Resonance in Medicine n/a
10. Chiang T, Messing RO, Chou WH (2011) Mouse model of middle cerebral artery occlusion. J Vis Exp. 10.3791/2761
11. Tabesh A, Jensen JH, Ardekani BA, Helpern JA (2011) Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn Reson Med 65:823-836
12. Gustafsson O, Montelius M, Starck G, Ljungberg M (2018) Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting. Magnetic Resonance in Medicine 79:1674-1683
Figures