Synopsis

Keywords: Microstructure, Diffusion/other diffusion imaging techniques, diffraction, disordered systems, exchange

We identify a new regime for the diffusion signal in non-confining disordered systems with locally varying diffusivity. It occurs at long times and large diffusion wavevectors, reminiscent of diffusion diffraction in closed pores. Remarkably, while for free diffusion the signal is exponentially strongly dephased, scattering off heterogeneities results in a much weaker, power-law decrease of the signal, thereby offering an enhanced sensitivity to the medium’s structure. In particular, we show how correlation functions of the medium’s microstructure to arbitrary order can be measured. We compare our theoretical predictions for the second order correlation function to numerical simulations with good agreement.

Introduction

How much can one learn about the structure of a complex medium by manipulating the gradients of Larmor frequency in an NMR experiment? This fundamental question is at the heart of microstructure mapping with diffusion MRI. As a well-known example, for diffusion in closed pores at long diffusion times, the diffusion signal is explicitly related to the pore shape function and exhibits characteristic peaks at specific $$$q$$$-values -- the phenomenon of diffusion diffraction¹.

Here we extend the notion of diffraction onto a non-confining geometry of arbitrarily varying diffusivity $$$D(\mathbf{r})$$$ by considering a previously unexplored "diffraction limit" of strong gradients, when a typical spin phase along its Brownian path is large. Remarkably, while for free diffusion the signal is exponentially strongly dephased, scattering off heterogeneities results in a much weaker, power-law decrease of the signal, thereby offering an enhanced sensitivity to the medium's structure.

Theory

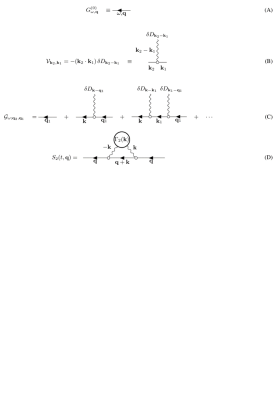
We consider arbitrary medium with the spatially varying diffusion coefficient $$$D(\mathbf{r})$$$ described by the diffusion equation $$\partial_t\psi_{t;\mathbf{r}}=\partial_\mathbf{r} \left( D(\mathbf{r}) \partial_\mathbf{r}\psi\right)\,,\quad D(\mathbf{r})=D+\delta D(\mathbf{r})\,.\qquad(1)$$

Using the effective medium formalism^2-4, we find the narrow-pulse signal to lowest order (2nd order) in the fluctuation $$$\delta D(\mathbf{r})/D$$$ (corresponding to the Feynman diagrams in Fig.1,
$$\delta S_2(t,\mathbf{q}) = \int_0^t \! \mathrm{d} t_2 \int_0^{t_2} \! \mathrm{d} t_1\, G^{(0)}_{t-t_2, \mathbf{q}} G^{(0)}_{t_1, \mathbf{q}} \int\! \frac{\mathrm{d}^d\mathbf{k}}{(2\pi)^d} \, \left[ \mathbf{q}(\mathbf{q}+\mathbf{k})\right]^2 \Gamma_2(\mathbf{k}) \, G^{(0)}_{t_2-t_1, \mathbf{q}+\mathbf{k}}\,.\qquad(2)$$
Here the power spectral density $$\label{Gamma-2}\Gamma_2(\mathbf{k}) = \frac1V\,\delta D(-\mathbf{k})\delta D(\mathbf{k})\qquad(3)$$$ is the Fourier transform of the correlation function $$$\Gamma_2(\mathbf{r}) = \left< \delta D(\mathbf{r}_0+\mathbf{r})\delta D(\mathbf{r}_0)\right>_{\mathbf{r}_0}$$$.

The cumulant expansion corresponds to both $$$\omega,q\to0$$$, with $$$q\to 0$$$ faster, formally defined as
$$\mbox{cumulant limit:} \quad \omega,q\to 0\,; \quad Dq^2/\omega \to 0 \,.$$
In this work, we are interested in the opposite, diffraction limit, where $$$q\to0$$$ slower than $$$\omega\to0$$$: $$\mbox{diffraction limit:}\quad \omega,q\to 0\,; \quad Dq^2/\omega \to \infty \,.$$ In this case, we are not operating with diffusion coefficient, kurtosis, etc, but we look at the whole signal, probing the system by large "momenta" (wavevectors) $$$\mathbf{q}$$$, whose associated length scale $$$1/q\ll L(t)=\sqrt{2Dt}$$$ is much smaller than the diffusion length $$$L(t)$$$.

In the diffraction limit, long $$$t$$$ effectively turns every free propagator inside momentum integrations, such as $$$G^{(0)}_{t_2-t_1, \mathbf{q}+\mathbf{k}}$$$ for the 2nd-order correction above, into a $$$\delta$$$-function of its momenta, i.e. $$$\sim \delta(\mathbf{q}+\mathbf{k})$$$. Assuming that $$$\Gamma_2(\mathbf{q})$$$ is slowly varying on the scale $$$1/L(t)$$$, we find our main result
$$S^{(1)}_2(t,\mathbf{q}) \simeq \frac{2\pi \Gamma_2(\mathbf{q})}{D^2q^2\, (4\pi Dt)^{d/2+1} }\,.\qquad(4)$$ Note that the correction (4) decreases merely as a power law in $$$t$$$ and $$$q$$$, in contrast to the usual exponential decay of the signal. Hence, remarkably, the nominally small correction to the free propagator becomes dominant at sufficiently large $$$Dq^2t\gg1$$$. This allows us to probe correlation functions such as $$$\Gamma_2(\mathbf{q})$$$ of the medium at finite $$$\mathbf{q}$$$.

Further analysis shows that higher order multiple diffusion encoding (MDE) sequences successively probe higher order correlation functions $$$\Gamma_n(\mathbf{q})$$$.

Monte Carlo simulations

MC simulations were carried out in one dimension with permeable membranes placed according to 2 universality classes, short range (Poissonian) and hyperuniform³, with mean barrier spacing $$$\bar{a}=2\mu$$$m over a $$$4\cdot10^4\mu$$$m sample. The diffusion coefficient was $$$D_0=1\mu$$$m²ms, time step $$$1\mu$$$s, permeability of the membranes was $$$\kappa=0.5\mu$$$m/ms leading to mean residence and diffusion times between two barriers of $$$\tau_R=\bar{a}/2\kappa=2ms$$$ and $$$\tau_D=\bar{a}^2/D_0=4$$$, respectively. Total simulated time was $$$T=100\tau_D=400ms$$$ using $10^9$ particles. All simulations were run in C++ CUDA on a NVIDIA Tesla V100 GPU.

Results

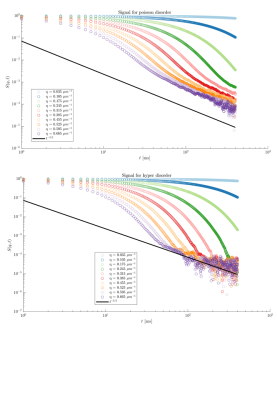
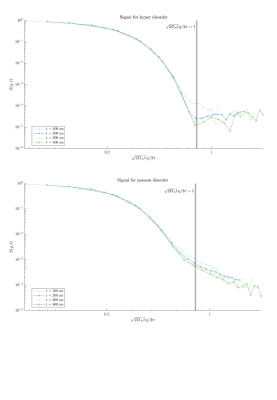
Figure 2 verifies that the exponential signal decay indeed changes to a much slower, power-law behavior as a function of diffusion time, Eq.(4), for sufficiently large $$$t$$$.

In Figure 3 we plot the dependence on $$$q$$$ which also conforms to theoretical predictions $$$\sim \Gamma_2(\mathbf{q})/ q^2$$$ of Eq.(4) for the larger values of $$$\sqrt{2D_\infty t}\,q/2\pi\sim\sqrt{b}$$$.

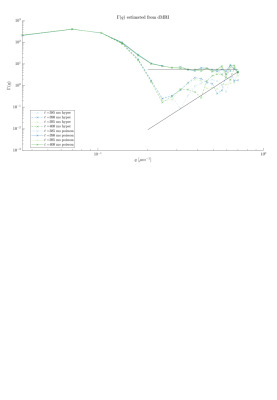
Finally, Figure 4 directly illustrates how Eq.(4) can be used to estimate $$$\Gamma_2(\mathbf{q})$$$ for a medium from the diffusion signal. Of course, such estimation works only for $$$q\gg 1/L(t)$$$.

Discussion and Conclusions

While we are used to, roughly, exponential decay of dMRI signal at strong diffusion weightings, it is not always so, and each example of specific, non-exponential functional form deserves special attention. Power-law dependencies always happen dueto specific reasons: diffusion-diffraction in a confined pore¹, $$$1/b$$$ scaling due to randomly oriented zero-radius fibers^5,6, Debye-Porod diffraction on a single barrier^7,8, presence of the voids in a porous medium⁹, and the localization regime¹⁰.

Here we uncover the diffraction-like phenomenon in a medium with smoothly varying local diffusivity $$$D(\mathbf{r})$$$. While perhaps less intuitive than coming from sharp boundaries, this phenomenon is due to scattering off a Fourier component $$$\delta D(\mathbf{q})$$$ that matches the $$$\mathbf{q}$$$-vector. In a disordered system, the spectrum of restrictions is continuous, and for any $$$\mathbf{q}$$$ there will exist the nonzero component $$$\delta D(\mathbf{q})$$$.

Recent developments of system with high-performance gradients are particularly exciting for exploring such physically compelling phenomena with the goal of deconvolving tissue micro geometry from the dMRI signal.