5016
Voxel-level denoising of diffusion MRI using a rank-1 decomposition1Department of Electrical Engineering, ESAT/PSI, KU Leuven, Leuven, Belgium, 2Medical Imaging Research Center, UZ Leuven, Leuven, Belgium, 3Translational MRI, Department of Imaging and Pathology, KU Leuven, Leuven, Belgium
Synopsis
Keywords: Diffusion/other diffusion imaging techniques, Signal Representations, Denoising
A voxel-wise rank-1 decomposition in spherical harmonics of the dMRI signal allows for a denoising method with minimal assumptions on signal and noise distributions. A voxel-wise denoising strategy is compared to MP-PCA on in vivo data and simulated data. The rank-1 decomposition and MP-PCA show visually similar results on the in vivo data, indicating that a voxel-level denoising approach has potential. However, results on the simulations differ. This may have various explanations; further investigation is necessary to strengthen the credibility of a rank-1 decomposition as a denoising approach.Introduction
Diffusion MRI (dMRI) inherently has low signal-to-noise ratios (SNR). Denoising is an important post-processing step to improve the SNR. Current denoising algorithms rely on assumptions about signal smoothness1,2 or assume homoscedastic noise in local patches3,4. Here, we explore a denoising strategy based on a voxel-wise rank-1 decomposition of multi-shell dMRI that imposes minimal assumptions on the signal and noise distribution. We evaluate this approach against MP-PCA4 denoising on simulated data and human in vivo brain imaging data.Methods
Rank-1 denoising. The dMRI signal in each voxel is projected onto an orthonormal basis of real, symmetric spherical harmonics $$$Y_\ell^m(n)$$$ of degree $$$\ell=0,2,…,\ell_{max}$$$ and index $$$m=-\ell,…,\ell$$$. The SH coefficients $$$s_{\ell,b}^m$$$ of individual shells $$$b$$$ are arranged in rows of matrices:$$
\mathbf{S}_\ell= \begin{bmatrix}s_{\ell,b_1}^{-\ell} & \cdots & s_{\ell,b_1}^{0} & \cdots & s_{\ell,b_1}^{\ell}\\ \vdots & & \vdots & & \vdots\\ s_{\ell,b_k}^{-\ell}& \cdots & s_{\ell,b_k}^{0} & \cdots & s_{\ell,b_k}^{\ell} \end{bmatrix}
$$
The singular value decomposition of matrices $$$S_\ell$$$ results in
$$
\mathbf{S}_\ell = \Sigma^r_{i=1}\mathbf{u}_{\ell,i}\mathbf{\sigma}_{\ell,i}\mathbf{v}_{\ell,i}^\top
$$
It has been shown – and validated in vivo – that these matrices $$$S_\ell$$$ are of rank = 1 under the broad assumption that all fascicles in the voxel share the same microstructure response up to a scaling factor5. Therefore, the leading left and right singular vectors $$$\mathbf{u}_{\ell,1}$$$ and $$$\mathbf{v}_{\ell,1}$$$ and the leading singular value $$$\sigma_{\ell,1}$$$ define a rank-1 signal decomposition that can be used to reconstruct the signal. This effectively results in a denoising operation, assuming the signal is adequately described by the first principal component and the noise resides in the remaining components.
MP-PCA denoising and Rank-1 denoising require a different order of preprocessing steps. MP-PCA is recommended as the first step in a processing pipeline because motion correction can introduce spatial correlations that violate the assumed Gaussian, uncorrelated noise. Rank-1 denoising is a voxel-wise decomposition technique that relies on good spatial alignment across different volumes and is therefore best applied after motion and distortion correction. Potential spatial noise correlations are not an issue because no assumptions on the noise distribution are made. Figure 1 visualises the processing pipeline for both methods.
Data. Human in vivo brain data of a single subject are obtained on a Philips 3T Achieva system. The diffusion encoding consists of 2 shells with b-values b=1000 and b=2000 $$$s/mm^2$$$, each with 128 uniformly spaced gradient directions and 2 b=0 reference images. The spatial resolution equals 1.875mm x 1.875mm x 2mm.
Experimental design. A simulated dataset is created based upon this in vivo data. The MP-PCA pipeline followed by MSMT-CSD6 is used to construct the ODFs and response functions. Forward spherical convolution of the ODFs and response functions was used to generate a ground truth image assumed to be noise free. The ground truth diffusion encoding consists of 3 shells with b-values of b=0, b=1000 and b=2000 $$$s/mm^2$$$, each with 60 uniformly spaced gradient directions. Additive Gaussian noise with a smooth unit-normalised spatial distribution was then generated at SNR=10, 20 and 50 (w.r.t. the mean b=0 signal) to produce noisy simulated images with known ground truth. All operations are performed full brain. The estimated noise level (root mean square (RMS) of residuals) was quantitatively compared to the simulated noise level.
Results
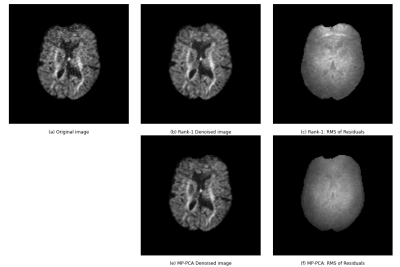
Figure 2 shows the results of the denoising algorithms on the simulated data. Increasing the noise levels negatively impacts the results of both denoising algorithms, although MP-PCA is less affected. Table 1 also supports this observation. The ratio σm/σTrue quantifies how well the estimated noise of method m approximates the simulated noise, where σm is the standard deviation of the RMS of the residuals of method m. Rank-1 denoising underestimates the noise level in comparison with MP-PCA.Figure 3 compares the in vivo data of rank-1 denoising and MP-PCA. The denoised images are the results of preprocessing according to the method’s respective pipeline as indicated in figure 1. The noise levels of rank-1 denoising have higher intensities than those of MP-PCA, as visible in figure 3.c and 3.f respectively.
Discussion
The use of a voxel-wise rank-1 decomposition as an alternative dMRI denoising method was investigated in this work on in vivo and simulated data. Results on the in vivo dataset showed visually similar results to MP-PCA denoising with little structure in the residuals in brain parenchyma. In simulations, however, the rank-1 approach underestimated the noise level while MP-PCA produced accurate estimates. The different performance in simulations and in vivo data may be due to the different gradient encoding scheme or due to the non-Gaussian noise distribution in magnitude dMRI data, and warrants further investigation.Future work can also investigate more direct use of the voxel-wise rank-1 representation in motion and distortion correction, tissue parameter mapping, and ODF estimation. Understanding noise propagation will contribute to the development of such methods.
Acknowledgements
No acknowledgement found.References
1. Aja-Fernández S, Pieçiak T, Vegas-Sánchez-Ferrero G. Spatially variant noise estimation in MRI: a homomorphic approach. Med Image Anal 2015; 20: 184– 197.
2. Tabelow K, Voss HU, Polzehl J. Local estimation of the noise level in MRI using structural adaptation. Med Image Anal 2015; 20: 76– 86.
3. Cordero-Grande, Lucilio, et al. ‘Complex Diffusion-Weighted Image Estimation via Matrix Recovery under General Noise Models’. NeuroImage, vol. 200, Oct. 2019, pp. 391–404.
4. Veraart, Jelle, et al. ‘Denoising of Diffusion MRI Using Random Matrix Theory’. NeuroImage, vol. 142, Nov. 2016, pp. 394–406.
5. Christiaens, Daan, et al. ‘On the Need for Bundle-Specific Microstructure Kernels in Diffusion MRI’. NeuroImage, vol. 208, Mar. 2020, p. 116460.
6. Jeurissen, Ben, et al. ‘Multi-Tissue Constrained Spherical Deconvolution for Improved Analysis of Multi-Shell Diffusion MRI Data’. NeuroImage, vol. 103, Dec. 2014, pp. 411–26.
Figures

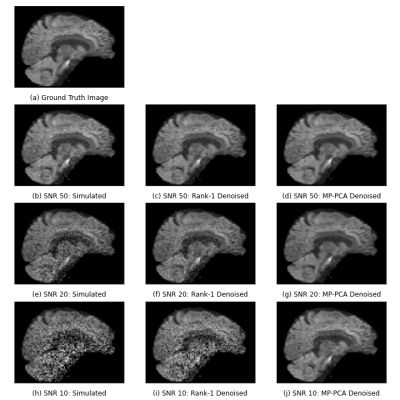
Figure 2: Comparison between rank-1 denoising and MP-PCA on the simulated dataset for various SNRs. Visually, MP-PCA outperforms rank-1, especially for higher SNR.