5006
Accelerated MRI thermometry guidance for transurethral ultrasound ablation of the prostate using locally low rank reconstruction
Ben YC Leung1, Robert M. Staruch1, and Mark Chiew2,3
1Profound Medical, Mississauga, ON, Canada, 2Medical Biophysics, University of Toronto, Toronto, ON, Canada, 3Physical Sciences, Sunnybrook Research Institute, Toronto, ON, Canada
1Profound Medical, Mississauga, ON, Canada, 2Medical Biophysics, University of Toronto, Toronto, ON, Canada, 3Physical Sciences, Sunnybrook Research Institute, Toronto, ON, Canada
Synopsis
Keywords: Thermometry, Interventional Devices, TULSA
MRI-guided transurethral ultrasound ablation of the prostate (TULSA) is controlled based on dynamic proton resonance frequency shift MR temperature imaging. Given the localized, but spatio-temporally coherent heating pattern, locally low rank (LLR) reconstruction could facilitate accelerated thermometry. Images acquired during TULSA in a phantom were retrospectively under-sampled by acceleration factors of R=3,4,6 by randomly sub-sampling EPI segments, and reconstructed using LLR constraints with non-overlapping 4D patches and cycle-spinning patch shifts. LLR reconstruction demonstrated lower variance than GRAPPA reconstructions in unheated regions, but increasing measurement bias at R≥4. In vivo investigation of LLR reconstruction of MR thermometry for TULSA is warranted.INTRODUCTION:
MRI-guided transurethral ultrasound ablation of the prostate (TULSA) is used for focal or whole-gland ablation in men with localized prostate cancer or benign prostatic hyperplasia. TULSA uses dynamic proton resonance frequency shift temperature imaging as input to a feedback control algorithm that automatically adjusts exposure parameters for 10 independent therapeutic ultrasound beams to achieve a confluent zone of coagulative heating between the ultrasound applicator and a prescribed target boundary. More efficient image acquisition could increase the imaging resolution or slice coverage of thermal monitoring, or decrease the imaging duty cycle within the same update rate for reduced SAR and hardware interference, and reduced sensitivity to peristalsis and respiratory motion. Given the localized, but spatio-temporally coherent energy deposition and thermal dissipation gradients of TULSA, image reconstruction using locally low rank (LLR) constraints could facilitate imaging at high acceleration factors with minimal loss of thermometry precision and accuracy.METHODS:
A commercially-available TULSA system (TULSA-PRO, Profound Medical) interfacing with a 3T scanner (Prisma, Siemens Healthineers) was used to heat a 90-degree sector of a tissue-mimicking gel phantom (Zerdine, CIRS) with continuous monitoring using the TULSA manufacturer’s temperature imaging sequence (fat-suppressed segmented echo-planar imaging, field of view 256x256mm, in-plane resolution 2x2mm, 12 axial slices with 4 mm thickness and 1 mm gap, TE 8.3ms, TR 40ms, flip angle 30°, EPI factor 13, dynamic update rate 6.2 seconds), using 10 channels of the Body 18 and Spine 32 receive coils. The treatment plan was prescribed to heat using 4 of the 10 ultrasound elements. During treatment delivery, ultrasound output and device rotation rate were automatically controlled by the TULSA software to achieve a temperature elevation of at least 20°C up to a target radius of 20 mm.Raw image data was retrospectively under-sampled at various acceleration factors for LLR reconstruction, using the fully-sampled data as a baseline reference. Under-sampling was performed by randomly sub-sampling EPI segments, simulating a realistic acceleration strategy using the same default temperature imaging sequence, at acceleration factors R=3, 4, and 6. The LLR reconstruction was posed as:
$$ \min_{x}\parallel E_x-d \parallel_2^2 + \lambda\sum_i\parallel R_ix \parallel _* $$
where E is the encoding operator incorporating sampling and coil sensitivities, x is the complex image time-series, d are the under-sampled k-space measurements, λ = 2.5e-4 is the LLR penalty parameter, $$$R_i$$$ is the patch extraction operator, with $$$i$$$ indexing over all image patches, and $$$‖∙‖_*$$$ is the nuclear norm. This was solved using the proximal optimized gradient method1, with a 4D patch size of [8, 8, 12, 25], with non-overlapping patches and cycle-spinning patch shifts every iteration.
Reconstruction was performed using a temporal window spanning the most recent 25 measurements. A separate fully-sampled calibration dataset with multiple time-points was acquired prior to heating, to estimate ESPIRiT coil sensitivity maps2 and identify an optimized range for the LLR penalty parameter λ. Comparison to conventional parallel imaging at R=3,4 was performed using a GRAPPA reconstruction.
Phase images reconstructed from fully and under-sampled data were used to calculate temperature difference maps based on the proton resonance frequency shift technique with a second-order drift correction. Temperature maps calculated from under-sampled reconstructions were compared to those from the fully-sampled dataset by the temporal standard deviation of temperature measurements in unheated regions (temperature uncertainty), and the difference of temperature measurements in heated regions (temperature accuracy).
RESULTS:
The LLR reconstructions demonstrated robust temperature estimation during ultrasound ablation at under-sampling factors up to R=6 (Fig. 2). In unheated regions, temperature estimates were unbiased for all reconstructions (worst case 0.01°C at R4 GRAPPA and 0.04° at R6 LRR). The LLR reconstructed data show significantly lower standard deviation (0.21°C at R=4) than equivalently accelerated GRAPPA reconstructions (1.5°C at R=4), which suffer from noise amplification (Fig. 3). When sampled along the target boundary, the LLR reconstruction exhibits a temperature offset that increases with acceleration factor, beyond 1°C at R=4 and above (Fig. 4). However, the denoising property of LLR reconstruction limits the observed variability in temperature estimates, particularly at higher acceleration factors, in effect trading bias for reduced variance.DISCUSSION:
Our data demonstrate that MR thermometry to monitor multi-element radial ultrasound heating can be accelerated with minimal impact on temperature measurement precision or accuracy using under-sampled acquisitions reconstructed with locally low rank constraints.The imaging speed of the proposed approach will be limited by image reconstruction time . Currently “real-time” LRR reconstruction on a laptop computer (Macbook Pro 2019) takes approximately 2 s/iteration, at least 5 iterations (10 s) to reach convergence when using prior dynamics as a “warm start” initialization. However, further optimization of LLR patch dimensions may reduce the computational demand, and the use of GPU parallel computing is expected to improve computational efficiency, as constraining the rank of image patches can be performed independently, in parallel.
Other low-rank approaches for accelerated MR thermometry have been proposed, such as a low-rank + sparse approach3. Further investigation into optimal low-rank reconstruction strategies, as well as their sensitivity to spatially heterogeneous tissues and coherent patterns of patient motion, are warranted.
CONCLUSION:
Locally low rank reconstruction is a promising technique for acceleration of proton resonance frequency shift MRI thermometry of radial heating patterns generated during transurethral ultrasound ablation.Acknowledgements
MC is supported by the Canada Research Chairs program. BL and RS are employed by Profound Medical.References
1. Taylor AB, Hendrickx JM, and Glineur F. Exact worst-case convergence rates of the proximal gradient method for composite convex minimization. J Optimization Theory and Applications. 2018;178:455-476.2. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT – an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magnetic Resonance in Medicine. 2014;71(3):990‐1001.
3. Cao Z, Gore JC, Grissom WA. Low-rank plus sparse compressed sensing for accelerated proton resonance frequency shift MR temperature imaging. Magnetic Resonance in Medicine. 2019;81(6):3555-3566.
Figures
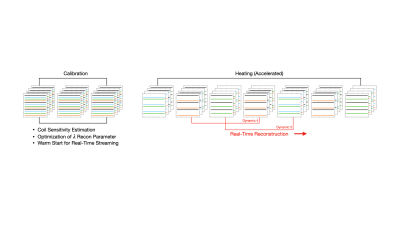
Schematic diagram of locally low rank reconstruction of under-sampled MRI thermometry data.
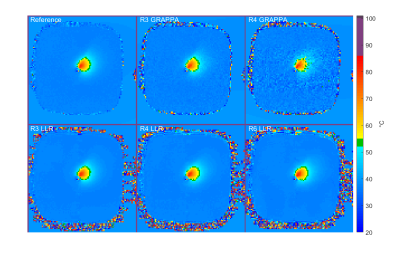
Example temperature maps calculated using fully-sampled (Reference), as well as GRAPPA and LLR reconstructions. Baseline temperature was artificially set to 37°C on all reconstructions.
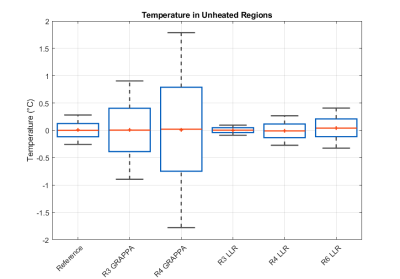
Temperature measurements in unheated regions of the phantom. Temperatures reported here are measured relative to baseline temperature as proton resonance frequency shift thermometry only measures temperature change from baseline.
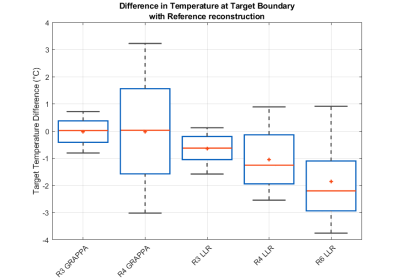
Differences in temperature at
the target boundary when compared to those measured on the Reference
reconstruction.
DOI: https://doi.org/10.58530/2023/5006