4973
Deep-learning-based Group-wise Motion Correction for Myocardial T1 Mapping
Eyal Hanania1, Lilach Barkat1, Israel Cohen1, Haim Azhari1, and Moti Freiman1
1The Technion – Israel Institute of Technology, Haifa, Israel
1The Technion – Israel Institute of Technology, Haifa, Israel
Synopsis
Keywords: Myocardium, Quantitative Imaging, Cardiac, Relaxation
Diffuse myocardial diseases can be diagnosed using T1 mapping technique. The T1 relaxation parameter is computed through the pixel-wise model fitting. Hence, pixel misalignment resulted by cardiac motion leads to an inaccurate T1 mapping. Therefore, registration is needed. However, standard registration methods are computationally expensive. To overcome this challenge, we propose a new deep-learning-based group-wise registration approach that register all the different time points simultaneously. Our approach achieved the best median model-fitting R2 compared to baseline methods (0.9846, vs. 0.9651/0.9744/0.9756), and achieve reasonably close T1 value to the expected myocardial T1 valueIntroduction
T1 relaxation time is a key source of soft tissue contrast in MRI. Mapping of each pixel T1 relaxation time, can depict relatively small variations within the cardiac muscle, highlight tissue pathology such as acute myocardial infarction, chronic scar tissue, or detect fatty infiltration. The T1 parameter has been emerged as a useful biomarker for various diffuse myocardial diseases1.Creating T1 mapping (Fig. 1) requires a time series of aligned images in which each pixel describes the same tissue across time. Nonetheless, during image acquisition there are inevitable cardiac motion, respiratory motion and involuntary patient motion2. Therefore there is a great need of image registration before the model fitting3.
The registration of a series of myocardial images is challenging due to the variations in contrast over different scanning times. Previously, nonrigid active shape model–based registration was suggested4 as well as using the T1 relaxation model approach2. Moreover, a deep-learning-based pair-wise registration network using Mutual Information (MI) as the loss function was also proposed5.
However, pairwise registration of the images acquired at different echo times may result in sub-optimal registration as the pairwise registration process does not leverage the information in the entire series.
In this work, we propose using a group-wise deep-neural-network for motion correction in quantitative cardiac T1 mapping. Our network gets the entire time series as input and registers all the images simultaneity to the reference image.
Data
We used a publicly available myocardial T1 mapping dataset5. The dataset includes 210 patients with known or suspected cardiovascular diseases. For each patient, 5 slices at 11 time points were available with their corresponding myocardial segmentation map. The imaging protocol was slice-interleaved T1 mapping sequence6 (STONE). In this protocol, 5 slices from base to apex in the short axis view were acquired at different 11 inversion times, resulting 11 T1w images for each slice location. The images were electrocardiogram triggered, with one slice image per RR interval. The sequence consists of repetitively multiple sets of five permute slices, each set acquired after a single inversion pulse6.Algorithms
The proposed method is a group-wise network10 that harnesses all the time series images as input for learning all the deformations field simultaneity. The multiple images were stacked along the channel axis and were inserted together into U-Net network (Fig. . The U-Net output was split into multiple separated heads of convolutional layers that produced a specific deformation field for each timestamp. The loss function minimized the sum of all MI calculations between all possible images to a fixed reference image. The loss can be calculated per pixel $$$p \in \Omega$$$ were $$$\Omega$$$ is all pixels from all patients. The group mutual information loss was calculated between the fixed image $$$I^{t_0}$$$ and the warped images $$$\{I^{t_i}\circ \phi_i|i=1,...,10\}$$$:The group-wise network loss is given by:
$$\mathcal{L} = \mathcal{L}_{GroupMI} + \lambda_{smooth} \cdot \mathcal{L}_{Smooth}$$
$$\mathcal{L}_{GroupMI}({I^{t_0},I^{t_i}\circ \phi_i|i=1,...,10\}) = -\sum_{i=1}^{10} \sum_{x \in I^{t_0}} \sum_{y \in I^{t_i}}p(x,y)log(\frac{p(x,y)}{p(x)p(y)})}$$
In order to find a realistic, smooth deformation field $$$\phi$$$, a regularization term was added. calculating the $$$l_2$$$ norm of the gradients of the deformation field $$$\phi$$$ per pixel.
$$\mathcal{L}_{smooth}(\phi) =\frac{1}{\Omega} \sum_{p \in \Omega}{||\nabla\phi(p)}||_2$$
Where $$$\lambda_{smooth}$$$ is an hyperparameter.
Experimental methodology
We cropped the images a size of 160 x 160 pixels for each time point as a preprocessing step. We normalized the images intensities using a min-max normalization, and saved the min and max values for post-processing restoration. We divided the 210 patients to 80\% as a training set and 20\% as a test set. To ensure the effectiveness of our method, we compared our results to the state-of-the-art deep learning algorithms for medical image registration including the pairwise VoxelMorph with mutual information loss7, and pairwise SynthMorph8, as well as with non-registered images. We evaluated the four methods by comparing the pixels R2 and T1 values.In our comparisons we assume that original unregistered images estimated median T1 value is closer to the actual median value. This is a reasonable assumption as, according to the imaging protocol, the images are relatively aligned with no significant movements during time9, 11.
Results
Table .1 summarized the mean and median values for the model fit quality (R2) and the T1 values. The entire distributions of these variables are presented in Fig. 2.The proposed method has a reasonably close T1 value to the original one and a significantly higher median R2 value with less variability than the compared methods. For the VoxelMorph and SynthMorph algorithms, although the mean R2 was higher than the non-registered images, the median R2 was lower, indicates an higher variation in the estimated T1 results as can be seen in the interquartile range in Fig. 2.Conclusion
Registration is a critical processing step in providing accurate myocardial T1 mapping. However, varying appearances over the different time points impose challenging registration task. In this work, we propose a group-wise registration network that produces multiple deformation fields simultaneously. Our experimental results on a publicly available cardiac T1 mapping of 210 patients show that our process significantly improves regressions R2 compared to state-of-the-art methods, while preserving reasonable T1 values. Our method was trained on myocardial T1 images but can extend to other quantitative MRI tasks.Acknowledgements
No acknowledgement found.References
- Taylor, A.J., Salerno, M., Dharmakumar, R., Jerosch-Herold, M.: T1 mapping:basic techniques and clinical applications. JACC: Cardiovascular Imaging 9(1),67–81 (2016)
- Tilborghs, S., Dresselaers, T., Claus, P., Claessen, G., Bogaert, J., Maes, F.,Suetens, P.: Robust motion correction for cardiac t1 and ecv mapping using at1 relaxation model approach. Medical Image Analysis 52, 212–227 (2019)
- Fu, Y., Lei, Y., Wang, T., Curran, W.J., Liu, T., Yang, X.: Deep learning in medicalimage registration: a review. Physics in Medicine & Biology 65(20), 20TR01 (2020)
- El-Rewaidy, H., Nezafat, M., Jang, J., Nakamori, S., Fahmy, A.S., Nezafat, R.:Nonrigid active shape model–based registration framework for motion correctionof cardiac t1 mapping. Magnetic resonance in medicine 80(2), 780–791 (2018)
- Arava, D., Masarwy, M., Khawaled, S., Freiman, M.: Deep-learning based motioncorrection for myocardial t 1 mapping. In: 2021 IEEE International Conference onMicrowaves, Antennas, Communications and Electronic Systems (COMCAS). pp.55–59. IEEE (2021)
- Weing ̈artner, S., Roujol, S., Ak ̧cakaya, M., Basha, T.A., Nezafat, R.: Free-breathingmultislice native myocardial t1 mapping using the slice-interleaved t1 (stone) se-quence. Magnetic resonance in medicine 74(1), 115–124 (2015)
- Balakrishnan, G., Zhao, A., Sabuncu, M.R., Guttag, J., Dalca, A.V.: Voxelmorph:a learning framework for deformable medical image registration. IEEE transactionson medical imaging 38(8), 1788–1800 (2019)
- Hoffmann, M., Billot, B., Greve, D.N., Iglesias, J.E., Fischl, B., Dalca, A.V.: Syn-thmorph: learning contrast-invariant registration without acquired images. IEEEtransactions on medical imaging 41(3), 543–558 (2021)
- Liu, J.M., Liu, A., Leal, J., McMillan, F., Francis, J., Greiser, A., Rider, O.J.,Myerson, S., Neubauer, S., Ferreira, V.M., et al.: Measurement of myocardial nativet1 in cardiovascular diseases and norm in 1291 subjects. Journal of CardiovascularMagnetic Resonance 19(1), 1–10 (2017)
- van der Ouderaa TF, Išgum I, Veldhuis WB, Vos BD. Deep Group-Wise Variational Diffeomorphic Image Registration. InInternational Workshop on Thoracic Image Analysis 2020 Oct 8 (pp. 155-164). Springer, Cham.
- Meloni, A., Martini, N., Positano, V., D’Angelo, G., Barison, A., Todiere, G.,Grigoratos, C., Barra, V., Pistoia, L., Gargani, L., et al.: Myocardial t1 valuesat 1.5 t: Normal values for general electric scanners and sex-related differences.Journal of Magnetic Resonance Imaging 54(5), 1486–1500 (2021)
Figures
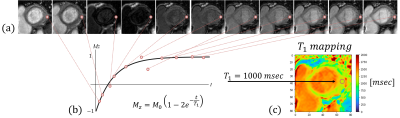
Figure 1: Schematic description of T1 mapping for a single pixel. (a) myocardial images at 11 sequential time points (displayed at their absolute value). (b) Fitting an inversion recovery curve of the magnetization Mz over different time points t and extracting the corresponding T1 and M0 parameters. (c) Displaying T1 mapping for all the pixels in the image.
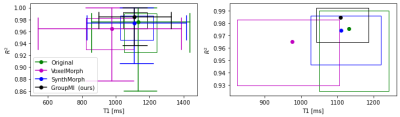
Figure 2: 2D boxplot comparing R2 and T1 value for different registration methods. (left) zoom out, (right) zoom in to the interquartile interval. Our GroupReg method achieves the highest median R2 value while keeping the T1 around the median of the original T1 values. The full circles are the intersection between T1 and R2 medians.
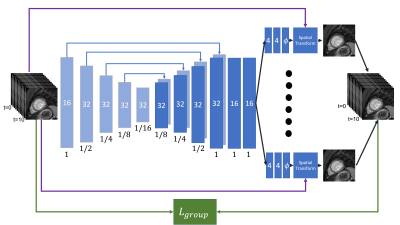
Figure 3: Illustration of our proposed network. Multiple images are stacked along the channel axis and inserted into the network. Each rectangle represents a convolutional layer. The filter numbers and the spatial resolution are printed in the rectangle center and below, respectively. The arrows stand for the skip connections between the encoder and the decoder. The U-Net output split into multiple heads of convolutional layers that produced a specific deformation field $$$\phi$$$ for each timestamp.

Table 1: Evaluation of the four algorithms according to R2 and T1 mean and median results.
DOI: https://doi.org/10.58530/2023/4973