4963
Low Rank Subspace-Constrained Compressed Sensing Reconstruction of Highly Accelerated Phase-Cycled bSSFP MRI for Fat Fraction Quantification
Eva S Peper1,2, Adèle LC Mackowiak1,2,3, Berk C Açıkgöz1,2, Nils Plähn1,2, Yasaman Safarkhanlo4, Li Feng5, and Jessica AM Bastiaansen1,2
1Department of Diagnostic, Interventional and Pediatric Radiology (DIPR), Inselspital, Bern University Hospital, University of Bern, Bern, Switzerland, 2Translation Imaging Center (TIC), Swiss Institute for Translational and Entrepreneurial Medicine, Bern, Switzerland, 3Department of Diagnostic and Interventional Radiology, Lausanne University Hospital (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 4Department of Cardiology, University Hospital Bern, Bern, Switzerland, 5BioMedical Engineering and Imaging Institute (BMEII), Department of Radiology, Icahn School of Medicine at Mount Sinai, New York, NY, United States
1Department of Diagnostic, Interventional and Pediatric Radiology (DIPR), Inselspital, Bern University Hospital, University of Bern, Bern, Switzerland, 2Translation Imaging Center (TIC), Swiss Institute for Translational and Entrepreneurial Medicine, Bern, Switzerland, 3Department of Diagnostic and Interventional Radiology, Lausanne University Hospital (CHUV) and University of Lausanne (UNIL), Lausanne, Switzerland, 4Department of Cardiology, University Hospital Bern, Bern, Switzerland, 5BioMedical Engineering and Imaging Institute (BMEII), Department of Radiology, Icahn School of Medicine at Mount Sinai, New York, NY, United States
Synopsis
Keywords: Image Reconstruction, Sparse & Low-Rank Models, bSSFP, phase-cycled bSSFP, subspace reconstruction
Fat fraction (FF) maps can be estimated from phase-cycled (PC) balanced steady-state free precession (bSSFP) imaging using a dictionary fitting approach (SPARCQ). Three-dimensional PC bSSFP imaging, however, is time consuming, since around 16 PCs must be sampled to fully describe a voxels’ PC profile. Compressed sensing (CS) has been proven to accelerate MRI scans. This study has two aims 1) to evaluate the performance of two CS algorithms (total variation (TV)- vs. subspace-constrained) taking regularisation along the PC dimension into account and 2) to investigate the upper limits of acceleration using these techniques on FF quantification using SPARCQ.Introduction
Proton density fat fraction (FF) is a quantitative image biomarker that allows to study the fat deposition in the body, e.g., for fatty liver disease [1]. It is defined as the sum of the fat proton signal divided by the sum of water and fat proton signals within an imaging voxel. Recently, it has been shown that the FF can be estimated from phase-cycled (PC) balanced steady-state free precession (bSSFP) imaging without prior knowledge of the fat model [2]. The method acquires multiple bSSFP images with consecutively changing RF phase, from which voxel-wise FF can be estimated using a dictionary fitting approach (SPARCQ) [2]. Three-dimensional PC bSSFP imaging, however, is time consuming, since ~16 PCs must be sampled [3]. Compressed sensing (CS) has been proven to accelerate scans by applying incoherent undersampling and iterative reconstruction [4,5]. It has been shown to be an advantage to add regularization constraints along inherently compressible data dimensions. This study has two aims: 1) to evaluate the performance of two CS algorithms (total variation (TV)- vs. subspace-constrained [6]) taking regularisation along the PC dimension into account and 2) to investigate the upper limits of acceleration using these techniques on FF quantification using SPARCQ.Methods
Cartesian 3D PC bSSFP images were acquired at 3T (Prisma, Siemens Healthineers, Erlangen, Germany). Firstly, a phantom with FFs of 0,0.20,0.39,0.58, 0.91 and 0.91 was scanned. Secondly, knee images of N=5 volunteers were acquired. The scan parameters were: 37 PCs with phase increments ranging from 0°-360° (steps of 10°) and TR=3.45 ms (optimized in [3]), TE=1.55 ms, 1.25x1.25x1.25 mm3 resolution, a matrix size of 128x128x80 and 20 min total scan time. The k-space of each fully-sampled PC bSSFP acquisition was undersampled retrospectively along the phase-encoding and PC dimension (Figure 1a) using a trajectory creating incoherent sampling patterns with acceleration factors of R=5,9,17,25 and 50. Then, a TV-constrained, and a subspace-constrained CS reconstruction [6] were applied separately along the PC dimension. The TV algorithm was formulated as:$$\mathbf{\tilde m} = \underset{\mathbf{\tilde m}}{\operatorname{argmin}}\frac{1}{2}\Vert\mathbf {F_UCm}- \mathbf y\Vert^2_2 - \lambda _1\Vert\mathbf {TVm}\Vert_1 $$
The algorithm solves for $$$\mathbf{\tilde m}$$$ the coil-combined image that is to be reconstructed. $$$\mathbf y$$$ is the undersampled multicoil k-space, $$$\mathbf {F_U}$$$ the Fourier transform including undersampling, $$$\mathbf {C}$$$ the coil combination operator, $$$\mathbf {TV}$$$ the sparsifying transform (finite differences) along the PC dimension, and $$$\lambda$$$ the regularisation weight. The subspace reconstruction follows the same notation, but additionally, the full image series $$$\mathbf m$$$ can be expressed as the full basis $$$\mathbf {UV}$$$ with $$$ \mathbf U \in \mathbf C^{PC \times PC}$$$ and $$$ \mathbf V \in \mathbf C^{N^3 \times N^3}$$$, or as a low rank subspace with K dominant basis components $$$\mathbf {U_KV_K}$$$ with $$$ \mathbf U \in \mathbf C^{PC \times K}$$$ and $$$ \mathbf V \in \mathbf C^{K \times N^3}$$$ .
$$\mathbf{\tilde{V}_K} = \underset{\mathbf {\tilde {V}_K}}{\operatorname{argmin}}\frac{1}{2}\Vert\mathbf {F_UC (U_KV_K)}- \mathbf y\Vert^2_2 - \lambda _2\Vert\mathbf {TV V_K}\Vert_1 $$
The algorithm is solved for $$$\mathbf {\tilde{V}_K}$$$ with a $$$\mathbf {TV}$$$ sparsifying transform, however, along the spatial dimension. For both methods, the regularisation weights and the number of iterations were optimized to $$$\lambda_1$$$=0.001, $$$\lambda_2$$$=0.001, and 42 iterations. K was optimized to be 12. For evaluation of the methods, the images were compared against the fully sampled reference (R=1). A region-of-interest (ROI) was drawn in the bone, muscle and subcutaneous fat and mean and standard deviation (SD) inside the ROI were compared between fully sampled and accelerated scans. Voxel-based dictionary fitting with simulated bSSFP profiles and M0, FF and water fraction (WF) maps were calculated from PC bSSFP data with the SPARCQ [2] framework (Figure 1b). A B0 correction was applied to the phantom data.
Results
bSSFP images were successfully reconstructed for both regularization methods for phantom and volunteer data (Figure 2). The expected FFs in the phantom vials could be reproduced up to R~25. Sharpness of small anatomical structures decreased with acceleration factor R. The bSSFP profiles were distinct for the three ROIs, and changed with increasing acceleration factors (Figure 3). The profile for bone and subcutaneous fat remained stable up to an acceleration factor of R~25, whereas the profile of the muscle region started to deteriorate at R~17. M0, FF and WF maps showed good image quality up to R~17 (Figure 4). In a statistical analysis of all volunteers (Figure 5) it could be seen that the mean value for the ROIs changed slightly with higher acceleration factors. The SD increased for higher acceleration factors and it was larger for the TV- than for the subspace-constrained reconstruction.Discussion
Subspace-constrained reconstructions maintained slightly higher image quality in comparison to TV at high acceleration rates. The algorithms performed better in fat than in water due to the higher SNR in fat regions as a result of the acquisition parameters, which can be adjusted. Reconstructions were done using a single, fully-sampled PC for sensitivity map estimation. This means a slightly longer overall scan time, but results in very high acceleration rates for the entire dataset.Conclusion
PC bSSFP scans can be accelerated up to an acceleration factor of R~17 with only minor changes in FF and WF quantification when using a subspace-constrained CS reconstruction, taking advantage of redundancies in the PC dimension.Acknowledgements
This study was supported by the Swiss National Science Foundation (grant number PCEFP2_194296).References
[1] Caussy C., Johansson L., Magnetic resonance-based biomarkers in nonalcoholic fatty liver disease and nonalcoholic steatohepatitis, Endocrinology, Diabetes & Metabolism, 2020 [2] Rossi GMC. et al., Fat fraction mapping using bSSFP Signal Profile Asymmetries for Robust multi-Compartment Quantification (SPARCQ), Magn. Reson. Med., 2020 [3] Mackowiak ALC. et al., Accelerated Fat fraction mapping using Signal Profile Asymmetries for Robust multi-Compartment Quantification (SPARCQ), Proc. Intl. Soc. Magn. Reson. Med., 2020 [4] Lustig M. et al, Sparse MRI: The application of compressed sensing for rapid MR imaging, Magn. Reson. Med., 2007 [5] Cukur T., Accelerated Phase-Cycled SSFP Imaging, IEEE, 2015[6] Feng L. et al., GRASP-Pro: imProving GRASP DCE-MRI through self-calibrating subspace-modeling and contrast phase automation, Magn. Reson. Med., 2020Figures
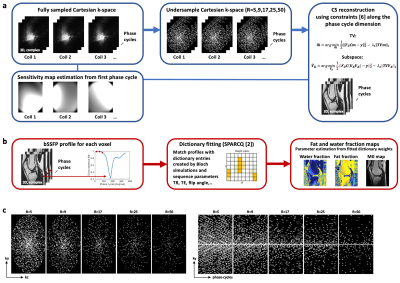
(a) Reconstruction pipeline starting with fully sampled multicoil k-space data from which a sensitivity map is estimated. Then undersampling and iterative CS reconstructions using TV and subspace [6] constraints are applied. (b) Fat fraction estimation using the SPARCQ framework [2]. (c) Incoherent Cartesian undersampling applied to the fully-sampled data. The left view shows the pattern for two phase encodings (ky,kz) and the right view for one phase encoding and the phase-cycle dimension (ky,phase-cycles). The readout dimension (kx) is fully sampled and not displayed.
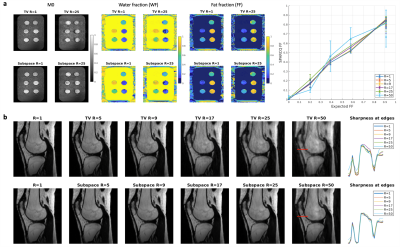
(a) Normalized, reconstructed M0, FF and WF maps for the water-fat phantom. The plot on the right shows deviations from the expected values for all acceleration factors R. (b) Normalized, reconstructed magnitude bSSFP images for all acceleration factors (R=5-50) for both regularisation methods (TV vs. subspace) in the first volunteer. The plots on the right show the profile and the sharpness of the magnitude images along the red line for all acceleration factors.
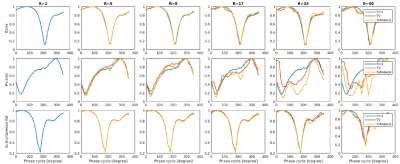
Normalized voxel-wise bSSFP profiles for each ROI (bone, muscle, subcutaneous fat) for all acceleration factors (R=5-50) and both regularisation methods (TV vs. subspace) in the first volunteer.
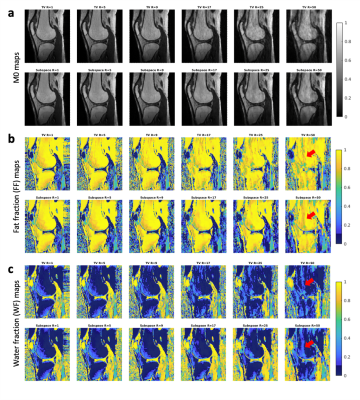
Normalized, reconstructed M0 (a), FF (b) and WF (c) maps for the first volunteer dataset, reconstructed for all acceleration factors (R=5-50) and using a TV- or a subspace-constrained regularization, respectively. Arrows indicated regions with larger deviations from the non-accelerated reference R=1. Remark: a water-fat swap is observed close to the knee cap due to insufficient B0 corrections of the volunteer scans, which however does not affect the acceleration rate comparison.
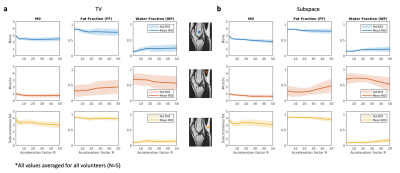
Statistical evaluation of M0, FF and WF maps in the ROIs of bone, muscle and subcutaneous fat. The mean and the SD of the values inside each ROI are plotted as a function of the acceleration factor R. Both, mean and SD, were averaged values for all 5 volunteers. Subplot (a) shows the results for TV-constrained and (b) for subspace-constrained reconstructions.
DOI: https://doi.org/10.58530/2023/4963