Synopsis

Keywords: Image Reconstruction, Brain

$$$T_{2}^{*}$$$ and quantitative susceptibility mapping are of increasing clinical interest, but typically require lengthy ME-GRE scans. To accelerate such acquisitions, we propose and implement a volumetric reconstruction method employing locally low rank (LLR) techniques to recover complex-valued ME images from highly undersampled k-space data that is suitable for parameter mapping. We present results for reconstructed magnitude and phase across multiple datasets and acceleration ratios, as well as computed $$$R_{2}^{*}$$$ and QSM from reconstructed images.

Introduction

$$$T_{2}^{*}$$$ mapping and quantitative susceptibility mapping (QSM) are increasingly employed clinically for diagnostic use. Examples include analysis of iron deposition in brain tissue as a potential indicator of Parkinson's disease [1][2], hemorrhage detection [3][4], and identification of age-related biomarkers of neurodegeneration [5][6][7]. Generation of these parameter maps typically requires three-dimensional (3D) multi-echo gradient-recalled echo (ME GRE) MRI acquisitions, which can be lengthy. Acquisitions that reduce scan times while preserving reconstruction quality are therefore of significant value. Locally low-rank (LLR) reconstruction methods [8][9], which exploit redundancy within local spatial patches of images to promote sparsity and constrain the solution space, have demonstrated promise in reconstructing images from undersampled k-space data. In this work, we propose a novel volumetric, multi-echo, complex-valued reconstruction method exploiting the low-rank properties of ME GRE magnitude and phase. An explicitly parameterized temporal signal model is first developed to promote low-rank behavior in magnitude reconstruction. We then develop and demonstrate a novel POCS [10] phase reconstruction incorporating multiple informed constraints.

Methods

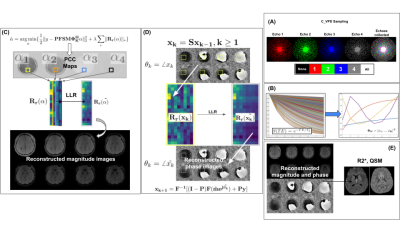
The magnitude reconstruction objective is given by:
$$\hat{\alpha} = arg min_{\alpha}\{ \frac{1}{2} \lVert y - \mathbf{P F S M \Phi}_{K}^{H} \alpha \rVert_{2}^{2} + \lambda \sum_{r} \lVert \mathbf{R_{r}}(\alpha) \rVert_{*} \}$$
where $$$\alpha$$$ are principal component coefficient (PCC) maps; $$$\mathbf{\Phi}_{K}^{H}$$$ is a truncated subspace basis of order $$$K<=n_{echoes}$$$; $$$\mathbf{M}$$$ is a complex exponential term corresponding to low-resolution phase estimated from the fully collected central k-space region; $$$\mathbf{S}$$$ denotes the coil sensitivity operator; $$$\mathbf{F}$$$ is the forward Fourier operator; $$$\mathbf{P}$$$ is the k-space sampling operator; $$$\mathbf{\lambda}$$$ is the LLR regularization parameter; $$$\vert \vert ... \vert \vert_{*}$$$ denotes the matrix nuclear norm; $$$\mathbf{R_{r}}(\alpha)$$$ is the forward Casorati operator on local PCC blocks at spatial index $$$\mathbf{r}$$$. Sampling was performed using complementary variable density Poisson Disc (C-VPD) sampling [11] as illustrated in Figure 1(a). To create the magnitude basis, simulated temporal signals were generated according to the monoexponential decay model $$$S(TE) = S_{0}e^{-\frac{TE}{T_{2}^{*}}}$$$, with $$$T_{2}^{*} $$$ ~ $$$\mathbf{U}$$$[1ms,1000ms] (Figure 1(b)). Principal Component Analysis (PCA) was performed on the ensemble of simulated signals to obtain an orthonormal basis ; $$$K=4$$$ principal components were chosen to form the truncated basis. Magnitude reconstruction was performed iteratively with ADMM [12] (Figure 1(c)). $$$T_{2}^{*}$$$ maps were subsequently generated with ARLO [13]. Phase images were reconstructed using a novel POCS-based scheme. Coupled with the reconstructed magnitudes $$$\hat{m} = \mathbf{\Phi}_{K}^{H}\hat{\alpha}$$$, the complex-valued echo images used in the phase reconstruction were initialized using zero-filled phase $$$\theta_{0}$$$ from the undersampled k-space: $$$x_{0} = \hat{m}e^{j\theta_{0}}$$$. Spatial consistency was enforced via the application of the sensitivity maps: $$$x_{k} = \mathbf{S}x_{k-1}$$$. The Casorati operator $$$\mathbf{R}_r$$$ was applied at each spatial index $$$r$$$ and singular value decomposition (SVD) was performed as shown in Figure 1(d): $$[u_{k,r},s_{k,r},v_{k,r}] = SVD[\mathbf{R}_{r}(x_{k})]$$ The singular values $$$s_{k,r}$$$ were soft-thresholded and the data was reprojected and reshaped into an array at spatial location $$$r$$$ via the backwards Casorati operator $$$\mathbf{R}_{r}^{T}$$$: $$\tilde{x}_{k,r} = \mathbf{R}_{r}^{T}(u_{k,r}\sigma_{\mu}(s_{k,r})v_{k,r})$$ where $$$\sigma_{\mu}$$$ denotes the soft-thresholding function. Phase was updated as $$$\theta_{k} = angle(\tilde{x}_{k})$$$ and consistency with both the acquired k-space values and the reconstructed magnitudes was enforced: $$x_{k} = F^{-1}[(\mathbf{I} -\mathbf{P})F(\hat{m}e^{j\theta_{k}}) + \mathbf{P}y]$$ where $$$\mathbf{I-P}$$$ is the elementwise complement of the k-space sampling mask. The raw phase maps were unwrapped using Laplacian-based phase unwrapping [14], local field maps were computed using V-SHARP normalized background phase removal [15], and QSM was performed using STAR QSM [16]. Normalized root mean square errors (NRMSE) were computed for each reconstruction result $$$\mathbf{x}_{recon}$$$: $$NRMSE(\mathbf{x}_{recon}) = \frac{1}{max(\mathbf{x}_{truth}) - min(\mathbf{x}_{truth})} \sqrt{\Sigma_{i}(\mathbf{x}_{recon}(i) - \mathbf{x}_{truth}(i))^2}$$ Five ME GRE datasets were used; four from a previous QSM study [17], and one new collection from a healthy subject on a 3T Siemens Skyra scanner with prior informed consent.

Results

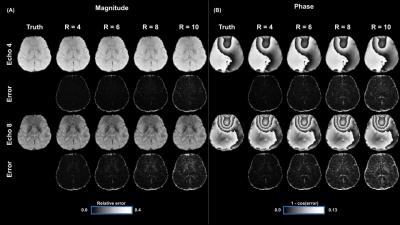
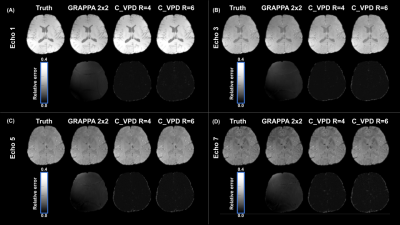
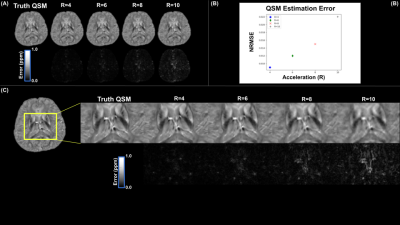
Figure 2(a-b) shows reconstructed magnitude and phase images on a single mid-axial slice for two echoes using C-VPD sampling with corresponding error maps for R values of 4,6,8, and 10. Normalized root mean square errors (NRMSE) across acceleration ratios were 0.007,0.009,0.013,0.026/0.073,0.10,0.150,0.21 for magnitude/phase (with cosine distance error used for phase). Figure 3(a-d) shows magnitude results for R = 4 and 6 against a 2x2 GRAPPA reconstruction with corresponding errors. Figure 4(a) illustrates $$$R_{2}^{*}$$$ results derived from reconstructed images with NRMSE values of 0.006,0.007,0.009,0.014 for R=4,6,8,10 (Figure 4(b)). Figure 5(a) shows QSM from reconstructed phase maps using acceleration ratios of R=4,6,8,10 resulting in NRMSE values of 0.009,0.012,0.015,0.022 (Figure 5(b)). Figures 4(c) and 5(c) show QSM and $$$R_{2}^{*}$$$ results for a magnified region of interest surrounding the thalamus.

Discussion

The LLR reconstruction method capably reconstructed images, even at higher R values, particularly in magnitude. Fine detail is preserved in the magnitude images, though there is a sharp drop in quality past R = 8. While GRAPPA 2x2 showed aliasing artifacts in the magnitude error maps, the LLR method using C-VPD at an equivalent or even higher R values showed no comparable large-scale error patterns. LLR with C-VPD shows excellent correspondence with truth in R2* and QSM, though there is some blurring in the maps at higher R values.

Conclusion

We have successfully developed and implemented a volumetric, complex-valued, multi-echo LLR reconstruction. Reconstructed images and derived parameter maps are highly accurate but exhibit some degradation at higher R values.

Acknowledgements

No acknowledgements.