4960
Model-based phase-difference reconstruction for accelerated phase-based T2 mapping
Xiaoqing Wang1,2, Jaejin Cho1,2, Yohan Jun1,2, Borjan Gagoski3, and Berkin Bilgic1,2
1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Fetal-Neonatal Neuroimaging and Developmental Science Center, Boston Children's Hospital, Harvard Medical School, Boston, MA, United States
1Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States, 3Fetal-Neonatal Neuroimaging and Developmental Science Center, Boston Children's Hospital, Harvard Medical School, Boston, MA, United States
Synopsis
Keywords: Image Reconstruction, Brain, model-based recontruction
Phase-based T2 mapping acquires two GRE volumes with opposite RF phase increments, then computes the phase difference and relates this to T2 values through Bloch modeling. We exploit the redundancy in these two acquisitions by posing this as a nonlinear inverse problem, and directly estimate the phase difference from k-space. This reduces the problem to the estimation of a complex M0 volume, and a real-valued phase difference, thus reducing the number of real-valued unknowns from 4 to 3 per voxel. The proposed reconstruction flexibly admits additional regularization, and yields higher quality images from undersampled acquisitions for rapid T2 mapping.Introduction
Quantitative T2 mapping is of great interest in clinical MRI. While conventional T2 mapping employs multi-echo spin-echo acquisition and utilizes magnitude images at various TEs for T2 estimation, a recent T2 mapping technique based on the phase difference of two distinct RF-spoiled steady-state gradient-echo acquisitions (with two different RF phases) has been proposed [1]. The phase-based method reconstructs two sets of complex images individually and is followed by phase difference calculation. In this work, instead of reconstructing two individual images for phase difference calculation, we propose to reconstruct the phase-difference maps directly from k-space by formulating image reconstruction as a nonlinear inverse problem. In such a way, the number of unknowns is reduced from two complex images to one complex and one real image. Moreover, sparsity constraints can be directly applied to the phase-difference maps, allowing for further acceleration.Methods
###MOdel-BAsed (MOBA) Phase-Difference ReconstructionPhase-based T2 mapping involves the acquisition of two GRE volumes with a small and opposite RF phase offset. These volumes can be described as:$$ Signal_1 = M0e^{i \phi + i \delta\theta} $$and$$ Signal_2 = M0e^{-i \phi + i \delta\theta} $$We define $$$B = M0e^{i \phi + i \delta\theta} $$$ thus making $$$ Signal_2 = B e^{2i \delta\theta}$$$. As such, we need to estimate the complex-valued $$$B$$$ and real-valued $$$\delta\theta$$$ during the reconstruction.When combined with the coil sensitivities $$$C$$$, Fourier encoding matrix $$$\mathcal{F}$$$ and $$$P$$$ is the subsampling mask:$$ F: {x} = {\big(B, \delta\theta\big)^{T}} \mapsto P\mathcal{F}C \cdot {B}\cdot e^{i\cdot 2\cdot {\delta\theta}}$$. We adopt the model-based reconstruction in BART [2,3] to estimate $$$B$$$ and $$$\delta\theta$$$ jointly from the two acquired GRE volumes and employ GPU acceleration. Fig1. demonstrates the data acquisition and image reconstruction strategy.
###Data acquisition
All data were acquired on a 3T Prisma system with 32ch reception. The pulse sequence was modified from a 3D-GRE product sequence so that RF phase increments and gradient spoiling moments could be adjusted [4]. All experiments used RF phase increments of +2 and -2 degrees. B1 corrections were performed for the flip angles using separately acquired B1 maps. Phantom data were obtained using a uniform fBIRN phantom at 1 mm iso. resolution with TE/TR = 2.62 / 10 ms and flip angle = 10 degrees, and FOV=192 x 192 x 168 mm3.In vivo data: a healthy volunteer was scanned at 1 mm iso. resolution and fully sampled data were obtained, which was retrospectively undersampled. The scan parameters include TE/TR = 2.62 / 10 ms and flip angle = 15 degrees, and FOV = 214 x 214 x 168 mm3.
Results
Fig2. depicts the results from the fBIRN phantom experiment. As anticipated, both phase difference and T2 map reconstructions are highly uniform in this phantom. Fully-sampled and R=4-fold accelerated MOBA T2 maps are highly similar, with mean values of 46 and 47 ms respectively. Fig3. compares M0 and phase difference estimates obtained from the proposed MOBA and SENSE reconstructions at R=4 with the fully-sampled data. MOBA is seen to closely match the fully-sampled reference, with improvements over SENSE in image quality, especially in the M0 map. Fig4. shows the estimated T2 maps from the two representative slices from Fig3. These were obtained using a pre-computed dictionary while incorporating B1 corrections. The high similarity is again observed in MOBA and the reference fully-sampled data.Discussion and Conclusion
We proposed a model-based reconstruction, MOBA to exploit redundancies in phase-based T2 mapping acquisitions. Since the acquired two GRE volumes differ only in their phase, we have capitalized on this to reduce the number of unknowns and jointly reconstructed a phase difference image directly out of the undersampled k-space data. MOBA flexibly admits additional regularization, is integrated with BART and can exploit GPU acceleration. It provided high quality T2 estimates from a moderate R=4-fold acceleration. Future directions include higher acceleration factors, deploying this acquisition at ultra high fields and wave encoded reconstructions to push the efficiency and resolution.Acknowledgements
This work was supported by research grants NIH R01 EB032378, R01 EB028797, R03 EB031175, U01 EB025162, P41 EB030006, U01 EB026996, and the NVidia Corporation for computing support.References
[1]. Wang X, Hernando D, and Scott R. Phase-based T2 mapping with gradient echo imaging. Magnetic Resonance in Medicine; 88 (2): 1015.
[2]. “BART Toolbox.” Accessed November 9, 2022. https://mrirecon.github.io/bart/.
[3]. Wang X, Tan Z, Scholand N, Roeloffs V, Uecker M. Physics-based reconstruction methods for magnetic resonance imaging. Philos. Trans. R. Soc.A 2021; 379:20200196.
[4]. Seginer A, and Schmidt R. Phase-Based Fast 3D High-Resolution Quantitative T2 MRI in 7 T Human Brain Imaging. Scientific Reports; 12 (1): 14088.
Figures
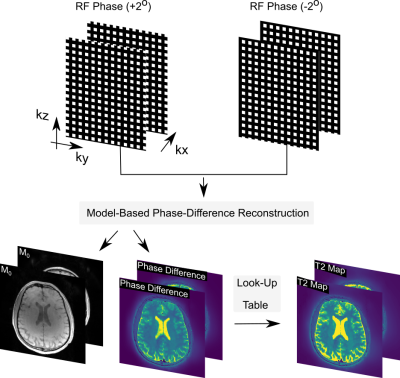
Fig 1. shows the overall data acquisition and image reconstruction strategy for phase-based T2 mapping with model based reconstruction.
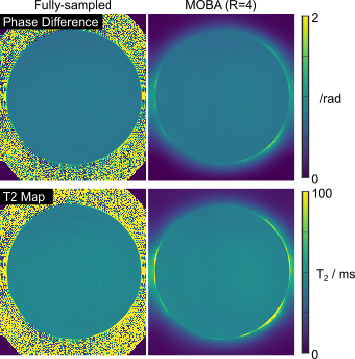
Fig2. Phase difference and T2 maps from the uniform fBRIN phantom. Quantitative T2 values are 46 +- 1 ms vs 47 +- ms for the fully-sampled and MOBA reconstruction at R=4.
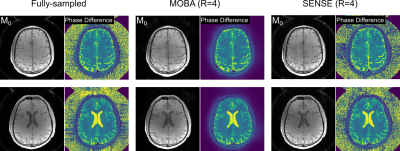
Fig3. Two representative slices from the in vivo experiment are shown. Proposed MOBA at R=4 yielded high quality M0 and phase difference estimates, with improvements over the standard SENSE reconstruction.
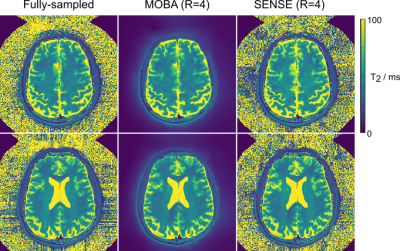
Fig4. T2 maps corresponding to the two slices shown in Fig3. MOBA has enabled high-quality mapping with high similarity to the fully-sampled reference maps.
DOI: https://doi.org/10.58530/2023/4960