Synopsis

Keywords: Image Reconstruction, Artifacts

Iterative undersampled MRI reconstructions, such as compressed sensing, can reconstruct undersampled MRIs - but due to their slow execution speed, they are not suitable for real-time applications. Several deep learning approaches have been proposed, mostly working in image space. Some of the approaches, which work on the k-space or in a mix of spaces, employ real-valued convolutions splitting the complex k-space into real and imaginary parts for processing - destroying the geometric relationship within the data. This research proposes Fourier-PD and Fourier-PDUNet models using complex-valued convolutions, which attempt to predict missing k-space frequencies and also to reduce artefacts in the image space.

Introduction

Magnetic resonance imaging (MRI) suffers from its inherent problem of slow acquisition speed, which can be improved with undersampling - by ignoring parts of the acquired k-space -that can lead to artefacts and loss of resolution. Several deep learning-based approaches have been proposed to reconstruct undersampled MRI, mostly focusing on artefact removal in image space, while also some approaches have been proposed that work in k-space or hybrid space (i.e. a mix of k-space and image space). k-space is always complex-valued, while image space can either be complex-valued or real-valued if only the magnitude image (or only the phase-image) is considered or if the magnitude and phase images are considered separately. Methods working in image space have mostly focused on correcting the magnitude images. Hence, real-valued convolution operations are sufficient. However, most of the approaches working in k-space¹ or even methods working in hybrid space² treat the complex-valued input as two separate real-valued data by splitting the complex data into real and imaginary parts and concatenating them on the channel dimension - discarding the richer algebraic structure of the complex data. This research proposes complex-valued neural networks to perform undersampled MRI reconstruction working in hybrid space.

Methods

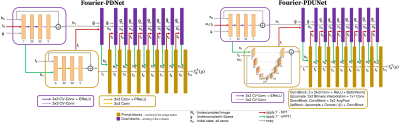
The original Primal-Dual network (PD Network)³, and the PD-UNet^4,5 were modified to propose Fourier-PD and Fourier-PDUNet architectures, shown in Fig.1, where the primal blocks work in image space, while the dual blocks work in k-space. Because k-space is complex-valued, the dual blocks of both these networks were modified by replacing the convolution layers with complex-valued convolution layers and PReLU activation functions with complex ReLU activations ($\mathbb{C}$ReLU). The primal blocks were identical to the original ones. The Fourier-PD and Fourier-PDUNet can be construed as an unrolled iterative reconstruction algorithm optimising both the k-space, as well as the image space.
During each step of the iteration, the processed k-Space (output of dual blocks) is reconstructed using iFFT and is combined with the previously processed image (output of primal blocks) to supply to the primal blocks. The output of the primal blocks is taken back to the k-Space using FFT, then combined with the processed k-Space and the original undersampled k-Space to supply to the dual blocks. The dual blocks optimise the k-Space - by trying to predict the missing frequencies, while the primal blocks optimise the image by trying to remove the artefacts. The output of the final primal block is the final reconstruction of the model. These models improve the quality of the reconstruction over iterations while also ensuring data consistency, similar to iterative reconstruction approaches, such as compressed sensing⁶. However, as these are learnt approaches with a fixed number of iterations, the reconstruction speed is not slow and may be used for real-time applications.
The models were trained by calculating the loss in image space by comparing the final reconstruction of the model against the ground-truth fully-sampled images with the help of L1 loss, which was minimised using the Adam optimiser (initial learning rate 0.001, decayed by 10 after every 25 epochs) with batch size one for 50 epochs. Once the models were trained, they were combined with the NCC1701 pipeline⁷ to apply a data consistency step to obtain the final result.
To evaluate this approach, T2w axial brain MRIs acquired at 3T with 16-channel coils with a matrix size of 768x396 from the fastMRI dataset were used and were artificially undersampled using 1D variable density sampling with acceleration factors 8 and 16. Currently, the proposed approach works with single-channel input. Hence, the fully-sampled, as well as the undersampled data, were combined using root-sum-of-squares after bringing them to image space and then they were again brought back to k-space after the coil-combination step.

Results

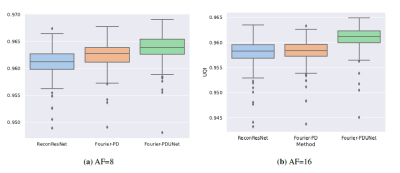
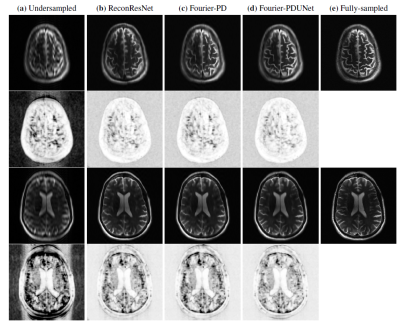
The performance of Fourier-PD and Fourier-PDUNet were compared against the undersampled reconstruction of the zero-filled k-space, as well as the ReconResNet⁷ model, which works only in image space. The quantitative evaluation is presented in Table 1 and Fig.2. The statistical significance of the differences was determined using the Mann-Whitney U-test, and it revealed that the best performing model Fourier-PDUNet achieved a statistically significant improvement over both ReconResNet and Fourier-PD for both acceleration factors. ReconResNet and Fourier-PD achieved similar scores - even though Fourier-PD got better scores for AF=8 and ReconResNet for AF=16, the differences were not statistically significant. A qualitative comparison has been shown in Fig.3.

Conclusion

This research proposed two complex-valued deep learning models working in the hybrid space of image and k-space and were compared against an image space model - ReconResNet model. Fourier-PDUNet achieved statistically significant improvements over both Fourier-PD and ReconResNet models, securing average SSIM values of 0.931±0.018 and 0.919±0.019, for acceleration factors 8 and 16, respectively. This research demonstrated the advantage of working in the hybrid space over pure image space. Further evaluations will be performed to compare the proposed models against other state-of-the-art models working in the k-space and hybrid space and also to evaluate the clinical applicability of these models. Moreover, the architectures will be compared against their real-valued counterparts by splitting the k-space into real and imaginary parts and also by treating the real-imaginary as the 3rd dimension of 2D MRIs - to evaluate the advantages of the complex-valued convolutions.

Acknowledgements

This work was in part conducted within the context of the International Graduate School MEMoRIAL at Otto von Guericke University (OVGU) Magdeburg, Germany, kindly supported by the European Structural and Investment Funds (ESF) under the programme ”Sachsen-Anhalt WISSENSCHAFT Internationalisierung” (project no. ZS/2016/08/80646).