Synopsis

Keywords: Image Reconstruction, Data Processing, Fast reconstruction algorithm

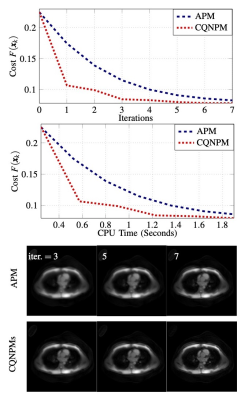
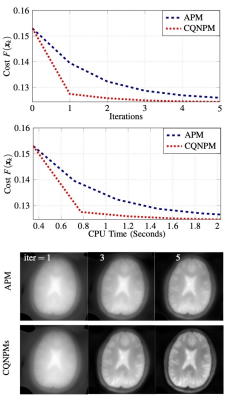
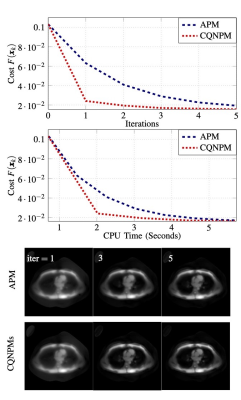
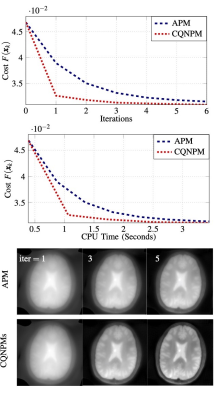
This work studies a complex quasi-Newton proximal method (CQNPM) for MRI reconstruction using wavelets or total variation (TV) based regularization. Our experiments show that our method is faster than the accelerated proximal method [1,2] in terms of iteration and CPU time.

Introduction

The reconstruction of compressed sensing MRI can be formulated as the following minimization problem: $$\min_{x\in\mathbb C^N}F(x),~F( x) \equiv \underbrace{\frac{1}{2}\|Ax-y\|_2^2}_{f(x)} + \lambda \, h(x),~~~~~~~~~(1)$$
where $$$A\in \mathbb C^{M\times N}$$$ refers to the forward model describing a mapping from the signal $$$x$$$ to the acquired data $$$y$$$ and $$$\lambda>0$$$ is the trade-off parameter. Here, we focus on $$$h(x)=\|T x\|_1$$$ for a wavelet transform $$$T$$$, or $$$h(x) = \text{TV}(x)$$$. Traditionally, one can use the accelerated proximal method (APM) [1,2] to solve (1). Here we propose a complex quasi-Newton proximal method to solve (1) even faster.

Methods

Denote a weighted proximal operator by $$\mathrm{Prox}_{\lambda h}^{W}(v)\equiv\arg\min_{x\in\mathbb C^{N}} \frac{1}{2}\|x-v\|_{W}^2 +\lambda h(x)~~~~~~~~~(2)$$ where $$$W\in \mathbb C^{N\times N}$$$ is a Hermitian positive definite matrix and $$$\|x\|_{W} = \sqrt{x'Wx}$$$ denotes the $$$W$$$-weighted Euclidean norm. When $$$W=I$$$, (2) becomes the well-known proximal operator. At the $$$k$$$th iteration, the CQNPM update is: $$x_{k+1} = \text{Prox}_{a_k\lambda h}^{B_k}\left(x_k-a_kB_k^{-1}\nabla_{x} f(x_k)\right)$$ where $$$a_k$$$ denotes the step-size. Here, the symmetric rank-$$$1$$$ method is used to compute $$$B_k$$$ [3] so that $$$B_k\in\mathbb C^{N\times N} \equiv D_k \pm u_k u_k'$$$ with $$$D_k$$$ a diagonal matrix and $$$u_k\in\mathbb C^{N}$$$.

For $$$h(\bar x)=\|\bar x\|_1$$$,one can solve (2) efficiently through the following lemma:
Lemma 1 [4]:
Let $$$W = D\pm uu'$$$. Then, $$\text{Prox}_{\lambda h}^{W}(x)=\text{Prox}_{\lambda h}^{D}(x\mp D^{-1}u\alpha^*),$$ where $$$\alpha^*\in\mathbb C$$$ is the unique zero of the following nonlinear equation $$$\mathbb J(\alpha):u'\left(x-\text{Prox}_{\lambda h}^{D}(x\mp D^{-1}u\alpha)\right)+\alpha.$$$
We solve $$$\mathbb J(\alpha) = 0$$$ using ``SciPy'' library in Python. When $$$h(x)=\|T x\|_1$$$ where $$$T$$$ is an invertible transform, we can rewrite (1) as $$$\frac{1}{2}\|AT^{-1}x-y\|_2^2 + \lambda \, \|x\|_1$$$ that Lemma 1 is still appliable.

For $$$h(x)=\text{TV}(x)$$$, we transform (2) to the following dual problem that is differentiable $$\begin{array}{rl} (P_1^*,Q_1^*,P_2^*,Q_2^*) =\arg\min\limits_{\substack{(P_1,Q_1)\in \mathcal P\\(P_2,Q_2)\in \mathcal P}} &\left\| \varphi (P_1,Q_1,P_2,Q_2)\right\|^2_{\tilde W}\end{array},~~~~~~~~~(4)$$
where $$${\tilde W}=\begin{bmatrix} \Re({W}) & -\Im({W}) \\ \Im({W}) & \Re({W}), \end{bmatrix},$$$ $$$\mathcal P$$$ denotes a set of real matrix-pairs $$$(P,Q)$$$ that satisfy $$\begin{array}{rl} P_{i,j}^2+Q_{i,j}^2\leq 1&~~\text{isotropic TV,}\\ |P_{i,j}|\leq1,~|Q_{i,j}|\leq1 & ~~\text{anisotropic TV},\end{array}$$ $$$\varphi(P_1,Q_1,P_2,Q_2)=\begin{bmatrix} \Re{(v)}\\ \Im{{(v)}} \end{bmatrix}-\lambda\left( \tilde{W}\right)^{-1} \begin{bmatrix}\text{vec}(\mathcal L(P_1,Q_1))\\ \text{vec}(\mathcal L(P_2,Q_2))\end{bmatrix},$$$ and $$$\mathcal L(P,Q)_{i,j}=P_{i,j}+Q_{i,j}-P_{i-1,j}-Q_{i,j-1}.$$$ Note that $$$\Re(\cdot)$$$ (respectively, $$$\Im(\cdot)$$$) refers to an operator to take the real (respectively, imaginary) partand $$$\text{vec}(\cdot)$$$ denotes the vectorization of a matrix. We compute $$$(\tilde{W})^{-1}$$$ in $$$\varphi(P_1,Q_1,P_2,Q_2)$$$ efficiently through the Schur complement since $$$W = D\pm u u'$$$. After solving (4), we reach
$$\begin{bmatrix} \Re(\text{Prox}_{\lambda h}^{W}(v))\\ \Im(\text{Prox}_{\lambda h}^{W}(v)) \end{bmatrix}=\varphi(P_1^*,Q_1^*,P_2^*,Q_2^*).$$

Results

All experiments are implemented in SigPy [5]. We used the data from [6]. Figures 1-4 show the results and experimental details.

Conclusion

For a general matrix $$$W$$$, solving (2) would be as hard as the original problem (1). By using the structure of $$$W$$$, i.e., $$$W=D\pm u u'$$$, we propose efficient approaches to address (2) when $$$h(x)=\|Tx\|_1$$$ or $$$\text{TV}(x)$$$. Compared with the computational cost in the proximal operator, i.e., $$$W=I$$$, the increased computation in (2) is insignificant, as illustrated by our CPU time comparisons.

Acknowledgements

This work is supported in part by R01 NS 112233.