Synopsis

Keywords: Image Reconstruction, Software Tools

We propose a new decomposition of the nuFFT algorithm, allowing for a zero-memory-overhead implementation of the (adjoint-)nuFFT. With one grid-sized buffer, the decomposition allows for a memory efficient nuFFT with negligible computational overhead compared to a two-fold oversampled conventional nuFFT - to the prize of less efficient parallelization on many-threads CPU systems. We reduce memory requirements of 3D non-Cartesian PICS-reconstructions in BART by a factor up to ten, allowing for GPU acceleration of reconstructions with eight coils and matrix size 256x256x256 on a 4GB consumer-level GPU.

Introduction

The non-uniform FFT (nuFFT) is at the heart of any non-Cartesian MRI reconstructions. Usual implementations of the nuFFT require an oversampled grid to prevent aliasing artifacts from the nuFFT itself, leading to a $$$(oN)^D$$$-memory overhead in D dimensions, such that especially 3D reconstrauctions are limited by the nuFFT memory requirement. In this work, we propose a decomposition of the nuFFT resulting either in a zero-memory-overhead nuFFT or a nuFFT using one buffer of size $$$N^D$$$ with theoretically no computational overhead compared to a $$$o=2$$$ oversampled nuFFT. The low-memory nuFFT is implemented in the BART [1] toolbox and, hence, can be used to reduce the memory-overhead of generic 3D-non-Cartesian Parallel-Imaging-Compressed-Sensing (PICS) reconstructions.

Theory

Implementations of the nuFFT usually employ the convolution theorem to split the non-uniform DFT into the application of a Cartesian FFT and a direct convolution with a small gridding kernel $$$W$$$, typically a Kaiser-Bessel window.[2, 3] In the continuous case, the forward mode of the non-uniform Fourier transform corresponds to
$$ \mathbf{\hat{f}}(k) = \left(W \ast \tilde{f}\right)(k) \qquad\text{with}\qquad \tilde{f}(x) = \frac{f(x)}{{\color{#E41A1C}{\hat{W}(x)}}}\;.$$
In the discretized setting, the field of view needs to be zero-padded by a factor $$$o$$$ to prevent aliasing artifacts, resulting in a memory overhead of $$$(oN)^D$$$. For $$$D=1$$$, the discretized nuFFT of the zero-padded vector $$$\tilde{f}_m'$$$ is then computed by
$$\begin{aligned}\hat{f}(k)&={}\sum_l{}W(k-l){}\sum_{m=0}^{oN}{}\exp\left(-\frac{2\pi{}i}{oN}l\left(m-\frac{oN}{2}\right)\right)\tilde{f}'_m\\&={}{\color{#FF7F00}{\sum_l{}W(k-l)}}{}{\color{#4DAF4A}{\exp\left(\pi{}i{}l\right)}}{}{\color{#377EB8}{\sum_{m=0}^{oN}{}\exp\left(-\frac{2\pi{}i}{oN}lm\right)}}{\color{#E41A1C}{\tilde{f}_m'}}\,,\end{aligned}$$
here the colors correspond to the operations visualized in Figure 1A). Instead of zero-padding $$$\tilde{f}_m$$$ in memory, we consider only the non-zero coefficients of $$$\tilde{f}'_m$$$ by restricting the sum of the factor $$$o=2$$$ oversampled FFT. By splitting even and odd frequencies, the FFT of size $$$2N$$$ is decomposed into two FFTs of size $$$N$$$[4], i.e. $$\begin{aligned}\hat{f}(k)&={}\sum_l{}W(k-l){}\sum_{m=0}^{N}{}\exp\left(-\frac{2\pi{}i}{2N}l\left(m-\frac{N}{2}\right)\right)\tilde{f}_m\\&={}{\color{#FF7F00}{\sum_{l'}{}W(k-2l')}}{}{\color{#4DAF4A}{\exp\left(-\frac{2\pi{}i}{2N}l'\right)}}{}{\color{#377EB8}{\sum_{m=0}^{N}{}\exp\left(-\frac{2\pi{}i}{N}l'm\right)}}{\color{#E41A1C}{\tilde{f}_m}}\\&+{}{\color{#FF7F00}{\sum_{l''}{}W(k-2l''{}-{}1)}}{}{\color{#4DAF4A}{\exp\left(-\frac{2\pi{}i}{2N}l''\right)}}{}{\color{#377EB8}{\sum_{m=0}^{N}{}\exp\left(-\frac{2\pi{}i}{N}l''m\right)}}{\color{#984EA3}{\exp\left(-\frac{2\pi}{2N}m{}+{}\frac{\pi{}i}{2}\right)}}{\color{#E41A1C}{\tilde{f}_m}}\,.\end{aligned}$$ In this equation, all phase-multiplications and the FFTs are linear, invertible, and can be performed in-place on the grid. Hence, by sequentially computing both interpolations, no memory buffer is required. Alternatively, the inversion steps can be skipped using one additional buffer of size $$$N^D$$$ as visualized in Figure 1B). The same decomposition can be used to save memory in the adjoint nuFFT or the Toeplitz-mode[5,6] of the forward-adjoint nuFFT. In $$$D$$$ dimensions, the nuFFT can be decomposed in $$$2^D$$$ steps which are computed sequentially.

Methods

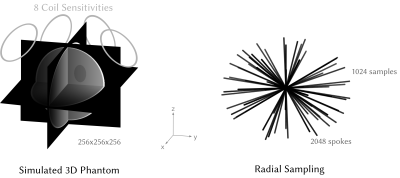
Comparison of nuFFT-Implementations
We evaluate the zero-overhead nuFFT implementation on a 256x256x256 voxel 3D Shepp-Logan phantom with $$$N_C=8$$$ coils, as visualized in Figure 2. We measure peak-memory and run-time of the CPU-implementations for the (adjoint-)nuFFT of BART with zero-memory-overhead, FINUFFT[7] and SigPy[8] on an Intel Xeon Gold 6132 processor using 32 threads. Similarly, we measure run-time and peak-memory for the GPU implementations of BART, gpuNUFFT[9], and SigPy on an Nvidia Tesla V100 GPU (32GB).

Low-Memory Modes in BART
We integrated the low-memory nuFFT implementation in the PICS tool to inverse problems of the form$$\mathbf{x}^*{}={}\text{argmin}_{\mathbf{x}}{}\sum_{i=1}^{N_C}\lVert{}\mathcal{PFC_i}{}\mathbf{x}{}-{}\mathbf{y}_i{}\rVert{}_2^2{}+{}\mathcal{R}(\mathbf{x})\;.$$Here, $$$\mathbf{x}$$$ is the volume to be reconstructed, $$$\mathcal{C}_i$$$ are the coil-sensitivity maps, $$$\mathbf{y}_i$$$ is the k-space data, $$$\mathcal{FP}$$$ is the non-Cartesian Fourier transform, and $$$\mathcal{R}(x)$$$ is the regularization. Typical iterative PICS reconstructions involve once the application of the adjoint $$$\mathcal{C}^H\mathcal{F}^H\mathcal{P}^H\mathbf{y}$$$ and afterwards multiple applications of the normal operator $$$\mathcal{C}^H\mathcal{F}^H\mathcal{P}^H\mathcal{PFC}$$$ in the iterations. The memory required for applying the normal operator with different implementations of the nuFFT is visualized in Figure 1. We measure peak-memory and reconstruction time for a CG-SENSE reconstruction with 30 CG-steps using four different modes, i.e.

• Normal: as in Figure 1C), but computing all phases in parallel;
• Low-mem: as in Figure 1C);
• Coil-Stack: as Low-mem but $$$N_C=1$$$ by looping over coils;
• Coil-Stack + No-Toeplitz: as in Figure 1B) with $$$N_C=1$$$.

In addition to the hardware described above, we use an Intel i7-6700K with 8 threads and an Nvidia Geforce GTX 670 GPU with 4GB.

Results

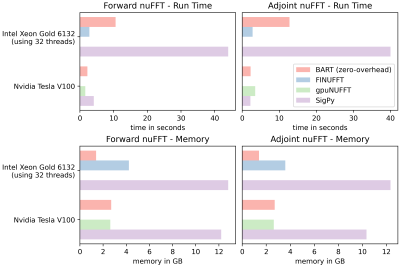
Comparison of nuFFT Implementations
Figure 3 presents the nuFFT performance measurements of the respective nuFFT implementations. The BART zero-memory-overhead implementation uses only 1.46GB memory. The FINUFFT is significantly faster but uses more memory.
On the GPU, BART requires additionally 1GB of memory as internal working space for the CUDA-FFT. BART and gpuNUFFT have similar computational performance and memory footprint.

Low-Memory Modes in BART
Memory and run-time measurements of the CG-SENSE reconstructions are presented in Figure 4. On the Xeon Gold 6132, each memory optimization increases the reconstruction time due to less efficient parallelization. On the i7-6700K, the same effect is observed for the Coil-Stacking vs. Low-mem mode. On the Tesla V100, the different modes behave similar, while CPU gridding is still dominated by the less efficient CPU parallelization. Memory optimizations allow for GPU acceleration on the GTX 670 GPU with 4GB, speeding-up the reconstruction by a factor of two compared to the CPUs.

Discussion and Conclusion

In this work, we presented a decomposition of the nuFFT algorithm allowing for a zero-memory-overhead implementation of the (adjoint-)nuFFT. Comparisons with state-of-the-art implementations show that BART's GPU-nuFFT is computationally competitive to the gpuNUFFT, while the CPU-nuFFT of BART has room for improvements. By integration of the low-memory implementation of the nuFFT and memory optimizations in the SENSE model, we have reduced the memory requirements of CG-SENSE reconstructions by a factor of up to ten, enabling non-Cartesian 3D reconstructions on consumer-level GPUs.