4908

Do deep learning-based qMRI parameter estimators improve clinical task performance?
Sean C. Epstein1,2, Timothy J. P. Bray3,4, Margaret Hall-Craggs3,4, and Hui Zhang1,2
1Computer Science, UCL, London, United Kingdom, 2Centre for Medical Image Computing, UCL, London, United Kingdom, 3Centre for Medical Imaging, UCL, London, United Kingdom, 4Imaging, UCLH, London, United Kingdom

Synopsis

Keywords: Machine Learning/Artificial Intelligence, Data Analysis

We compare modern deep learning (DL)-based parameter-estimation methods to their traditional maximum-likelihood estimation (MLE) counterparts by evaluating each approach’s performance in two clinical classification tasks. This is motivated by recent work demonstrating the inherent bias-variance trade-off that differentiates different DL-based approaches. Results show how these trade-offs manifest in the ‘real world’ of tissue classification, and how they compare to the performance achievable with conventional iterative MLE.

INTRODUCTION

Quantitative MRI (qMRI) is increasingly relying on deep learning (DL) for rapid model parameter estimation1. However, as well as reducing computation time, DL approaches also differ from conventional methods in the values of the estimated qMRI parameters themselves. Recent work1 has shown that these differences vary systematically across different DL parameter estimators: some approaches produce high-bias low-variance parameter estimates, whereas others have the opposite effect.

However, it is still unclear how these methods perform when applied to real-world clinical tasks such as tissue classification/subtyping. Previous work has shown that the task performance of different parameter estimation methods can be assessed accurately in silico, but its scope was limited to conventional fitting2.

The present work applies this previously-developed task-driven assessment framework to DL parameter-estimation methods, and compares their performance to conventional fitting approaches.

METHODS

Five parameter estimation methods (three DL, two conventional) were compared and assessed on their performance in two qMRI classification tasks. These tasks consisted classifying and subtyping spondyloarthritis (SpA), an inflammatory disease affecting bone marrow around the sacroiliac joints, using diffusion-weighted MRI. The relevant diffusion signal model is intravoxel incoherent motion (IVIM):
$$S(b) = S_0 ( f e^{-b (D_{slow} + D_{fast})} + (1 – f)e^{-b D_{slow}})$$
Following the methods outlined in previous work2, 25,000 noisy IVIM signals were synthesied for four SpA subtypes and matched pairwise to simulate two classification tasks (Table 1). The IVIM model was fit to these signals independently using the 5 aforementioned parameter estimation methods: two conventional3 (bound-constrained non-linear least squares, segmented non-linear least squares) and three deep learning1(SupervisedGT, SupervisedMLE, Self-supervised).

The IVIM parameter estimates produced by each method were used to calculate ROC curves for the two classification tasks. The relative performance of each method was summarised by the area under the curve (AUC) and analysed by visualising the distribution of parameter estimates under noise.

RESULTS & DISCUSSION

Figure 1 summarises the performance of each parameter estimation method. Task 1 classifies tissues based on differences in perfusion fraction f, whereas task 2 relies on differences in estimated diffusivity DSlow.

It can be seen that all DL parameter estimation methods outperform straightforward bound-constrained MLE estimation (bcNLLS), and in the case of Task 2, also outperform ‘modified’ two-step MLE estimation (sNLLS). For both tasks, a neural network trained in a supervised manner on groundtruth labels (SupervisedGT) maximises classification performance (highest AUC). These findings are explained in Figure 2, which shows the distribution of each method’s parameter estimates under 25,000 noise instantiations.

Tissue classification relies on the ability to separate the two distributions, represented by solid and dashed lines. In both tasks, conventional estimators are associated with broader (higher variance) distributions than DL methods. True maximum-likelihood estimation (bcNLLS) is also associated with smallest relative bias between tissues (Δμ).

Based on previous work1, we expect two classes of DL methods: SupervisedMLE and Self-supervised (higher variance, lower absolute and relative bias) on the one hand, SupervisedGT (lower variance, higher absolute and relative bias) on the other. Our results confirm this hypothesis. SupervisedGT achieves the highest task performance by minimising variance under noise (σ), which in this case outweighs the associated increase in both absolute and relative bias.

CONCLUSIONS

We compare DL qMRI parameter estimation methods to traditional model fitting by assessing each method’s performance across two clinical classification tasks.

We show that, as a class of methods, DL estimators outperform traditional approaches not only in computational cost, but also in classification task performance; this is achieved by reducing the variance of parameter estimates under noise.

Furthermore, we confirm previously-reported1,4–6 findings that variation between different DL approaches can be analysed through the lens of a bias-variance trade-off: training networks with groundtruth labels minimises variance, whereas using MLE labels optimises bias.

In the present work, variance-minimising groundtruth-labelled networks are found to maximise task performance, but this trade-off may not always be optimal. In light of this we propose selecting parameter estimation methods – in the case of DL approaches, selecting the training labels – to maximise the performance of the qMRI task at hand.

Acknowledgements

No acknowledgement found.

References

  1. Epstein SC, Bray TJP, Hall-Craggs M, Zhang H. Choice of training label matters: how to best use deep learning for quantitative MRI parameter estimation. Published online May 11, 2022. doi:doi.org/10.48550/arXiv.2205.05587
  2. Epstein SC, Bray TJP, Hall-Craggs MA, Zhang H. Task-driven assessment of experimental designs in diffusion MRI: A computational framework. PLoS One. 2021;16(10):e0258442. doi:10.1371/JOURNAL.PONE.0258442
  3. Suo S, Lin N, Wang H, et al. Intravoxel incoherent motion diffusion-weighted MR imaging of breast cancer at 3.0 tesla: Comparison of different curve-fitting methods. J Magn Reson Imaging. 2015;42(2):362-370. doi:10.1002/jmri.24799
  4. Barbieri S, Gurney‐Champion OJ, Klaassen R, Thoeny HC. Deep learning how to fit an intravoxel incoherent motion model to diffusion‐weighted MRI. Magn Reson Med. 2020;83(1):312-321. doi:10.1002/mrm.27910
  5. Grussu F, Battiston M, Palombo M, Schneider T, Wheeler-Kingshott CAMG, Alexander DC. Deep Learning Model Fitting for Diffusion-Relaxometry: A Comparative Study. Math Vis. Published online 2021:159-172. doi:10.1007/978-3-030-73018-5_13
  6. Gyori NG, Palombo M, Clark CA, Zhang H, Alexander DC. Training data distribution significantly impacts the estimation of tissue microstructure with machine learning. Magn Reson Med. 2021;00:1-16. doi:10.1002/MRM.29014

Figures

Figure 1 - ROC curves and associated AUC values for the two clinical classification tasks described in Table 1


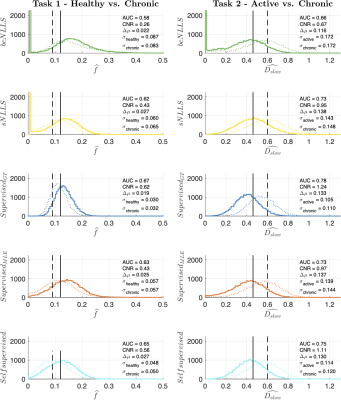
Figure 2 - Distribution of parameter estimates used to calculate each task's ROC curves in Figure 1

Table 1 - Classification tasks 1 and 2. Synthetic signals corresponding to each tissue were generated and 25,000 noise Rician noise instantiations were simulated

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
4908
DOI: https://doi.org/10.58530/2023/4908