4904
B1 and B0 insensitive R1σ preparation pulses can reduce sensitivity to R1σ dispersion
Kevin D Harkins1,2,3, Jason Ostenson1,2, Fatemeh Adelnia1,2, Feng Wang1,2, Zhongliang Zu1,2, and John C Gore1,2,3
1Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, 2Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, 3Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
1Radiology and Radiological Sciences, Vanderbilt University Medical Center, Nashville, TN, United States, 2Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, 3Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
Keywords: Relaxometry, Simulations
R1σ dispersion imaging can be used to uncover specific relaxation mechanisms in soft tissues, but is sensitive to B0 and B1 inhomogeneity. Several varieties of R1σ preparation pulses have been developed to reduce sensitivity to B0 and B1, typically by introducing a spin echo or double spin echo as part of the preparation pulse. This simulation study shows that such pulses can actually reduce the sensitivity to R1σ dispersion.Introduction
$$$R_{1\rho}$$$ dispersion imaging holds promise to increase the sensitivity of MRI to changes in soft tissues by emphasizing specific relaxation mechanisms. Two regimes of $$$R_{1\rho}$$$ are known to be relevant in tissue: the diffusion regime, where transverse dephasing is accelerated by water diffusion across microstructural susceptibility gradients; and the chemical exchange regime, where transverse relaxation is accelerated by water proton exchange with metabolites or macromolecules1. Traditional spin locking pulses are sensitive to inhomogeneities in $$$B_0$$$ and $$$B_1$$$, so accurate characterization of $$$R_{1\rho}$$$ dispersion is technically challenging. To reduce these challenges, a number of studies have developed novel $$$R_{1\rho}$$$ preparation pulses that are less sensitive to $$$B_0$$$ and $$$B_1$$$, usually by combining a single or double spin echo period with phase cycling of pulses during preparation2-4. Example preparation schemes are shown in Figure 1. While these pulses do reduce sensitivity to inhomogeneities to $$$B_0$$$ and $$$B_1$$$, there is potential for these pulses to reduce the sensitivity to relaxation processes of interest.This study compares the analytic model for $$$R_{1\rho}$$$ dispersion in the diffusion regime with simulations of $$$R_{1\rho}$$$ dispersion for three common $$$R_{1\rho}$$$ preparation pulses: traditional spin locking pulse, spin locking pulses with a spin echo, and spin locking pulses with a double spin echo.
Methods
The analytic model for $$$R_{1\rho}$$$ dispersion in the diffusion regime is given by5$$R_{1\rho} = R_2 + \frac{\gamma^2g^2D}{(q^2D)^2+\omega_1^2}$$
where $$$R_2$$$ is the transverse relaxation rate, $$$\gamma$$$ is the gyromagnetic ratio, $$$g$$$ is the mean gradient strength of the $$$B$$$ field, $$$\omega_1$$$ is the spin lock frequency, and $$$D$$$ is the diffusion coefficient. $$$q$$$ is the spatial frequency over which $$$B$$$ varies, where $$$L=2\pi/q$$$ is the characteristic length scale over which the field $$$B$$$ varies.
To compare the analytic model with the three different preparation schemes, simulations of coupled Bloch equations were performed with a sinusoidally oscillating $$$B$$$ field over a defined length scale, $$$L$$$, with mean gradient strength $$$g$$$. Over a spatial dimension, $$$x$$$, the magnetic field terms are given by
$$
B(x)=
\begin{bmatrix}
0 & b_0(x) & -b_{1\mathrm{y}} \\
-b_0(x) & 0 & b_{1\mathrm{x}} \\
b_{1\mathrm{y}} & -b_{1\mathrm{x}} & 0
\end{bmatrix}
$$
where $$$b_{1\mathrm{x}}$$$ and $$$b_{1\mathrm{y}}$$$ are the x and y components of the applied RF puplse, and $$$b_0$$$ is the sinusoidally varying background magnetic field strength5,
$$b_0(x)=\sqrt{2}\frac{g}{q}\sin(qx).$$
A relaxation matrix is given by $$$R=\mathrm{diag}[R_2;R_2;R_1]$$$, and the exchange matrix is determined by diffusion, $$$K=D/\Delta x^2 I_3$$$. Given $$$N$$$ spatial compartments over the length, $$$L$$$, a full system matrix is given by
$$
A=
\begin{bmatrix}
U(x_0) & K & 0 & \cdots & 0 & K\\
K & U(x_1) & K & \cdots & 0 & 0\\
0 & K & L(x_2) & \cdots & 0 & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & \cdots & U(x_{N-2}) & K\\
K & 0 & 0 & \cdots & K & U(x_{N-1})\\
\end{bmatrix}
$$
where the block matrices on the diagonal are $$$U(x) = \gamma B(x)-R-2K$$$. The coupled Bloch equations are then given by
$$\frac{d\overrightarrow M}{dt} = A\overrightarrow M-\overrightarrow M_0,$$
where $$$M$$$ is a column vector of length 3N, consisting of repeated $$$[M_x(x);M_y(x);M_z(x)]$$$.
For constant matrix terms, the general solution to the coupled Bloch equations is
$$\overrightarrow{M}(t) = e^{At}(\overrightarrow{M}_i-\overrightarrow{M}_{ss}) + \overrightarrow{M}_{ss}$$
where $$$\overrightarrow{M}_i$$$ is the initial condition, $$$e$$$ the matrix exponential operation, and $$$\overrightarrow M_\mathrm{ss} = -A^{-1} R \overrightarrow M_0$$$.
The analytic solution to dispersion in the diffusion regime was compared with numerical solutions to the coupled Bloch simulations for a range of spin lock time, TSL = 5:5:100 ms, with spin lock frequency (FSL) given by 17 log spaced points between 1 Hz and 10 kHz. Tissue parameters were: $$$T_2$$$ = 50 ms, $$$D=2.0$$$ $$$\mu$$$m$$$^2$$$/ms, and $$$B_0$$$ and $$$B_1$$$ inhomogeneity were neglected. $$$L$$$ was simulated for a range between 5-50 $$$\mu$$$m. Simulated signals vs TSL were fit to a relaxation time constant. $$$R_{1\rho}$$$ dispersion with FSL was fit to estimate model parameters, $$$\tilde g$$$ and $$$\tilde q$$$.
Results
A comparison of simulated vs analytic signal for $$$R_{1\rho}$$$ dispersion is shown in Figure 2. While there is good agreement between simulation and the analytic model for the traditional spin lock pulse, the magnitude of $$$R_{1\rho}$$$ dispersion is apparently decreased by the introduction of the spin echo or double spin echo preparation.Full $$$R_{1\rho}$$$ dispersion curves are shown for $$$L\approx$$$ 5, 16 and 25 $$$\mu$$$m in Figure 3, where at larger $$$L$$$ (or smaller $$$q$$$) the magnitude of the $$$R_{1\rho}$$$ dispersion is influenced by the choice in preparation pulse. The ratio of estimated and actual model parameters is given in Figure 4.
Discussion and Conclusions
This simulation study illustrates that care must be used in applying $$$B_0$$$ and $$$B_1$$$ insensitive pulses for measuring $$$R_{1\rho}$$$ dispersion. For relatively slow exchanging regimes, the amount of dispersion can be reduced by the introduction of spin echo periods into the preparation pulse. In essence, if exchange is too slow, the spin echo or double spin echo periods serve to refocus some of the $$$R_{1\rho}$$$ relaxing signals. Future studies should explore methods to correct for such biases or investigate new methods to reduce sensitivity of $$$R_{1\rho}$$$ dispersion to $$$B_0$$$ and $$$B_1$$$ without influencing $$$R_{1\rho}$$$ dispersion.Acknowledgements
This work was supported by NIH R01EB024525References
1. Spear, J. T., & Gore, J. C. (2016). New insights into rotating frame relaxation at high field. NMR in Biomedicine, 29(9), 1258–1273. https://doi.org/10.1002/nbm.34902. Witschey, W. R. T., Borthakur, A., Elliott, M. A., Mellon, E., Niyogi, S., Wallman, D. J., Wang, C., & Reddy, R. (2007). Artifacts in T1ρ-weighted imaging: Compensation for B1 and B0 field imperfections. Journal of Magnetic Resonance, 186(1), 75–85. https://doi.org/10.1016/j.jmr.2007.01.015
3. Pang, Y. (2022). A self-compensated spin-locking scheme for quantitative R1 dispersion MR imaging in ordered tissues. Magnetic Resonance Imaging, 94(September), 112–118. https://doi.org/10.1016/j.mri.2022.09.007
4. Wang, K., Zhang, W., Li, S., Jin, H., Jin, Y., Wang, L., Li, R., Yang, Y., Zheng, J., & Cheng, J. (2022). Noncontrast T1ρ dispersion imaging is sensitive to diffuse fibrosis: A cardiovascular magnetic resonance study at 3T in hypertrophic cardiomyopathy. Magnetic Resonance Imaging, 91(December 2021), 1–8. https://doi.org/10.1016/j.mri.2022.05.001
5. Spear, J. T., Zu, Z., & Gore, J. C. (2014). Dispersion of relaxation rates in the rotating frame under the action of spin-locking pulses and diffusion in inhomogeneous magnetic fields. Magnetic Resonance in Medicine, 71(5), 1906–1911. https://doi.org/10.1002/mrm.24837
Figures
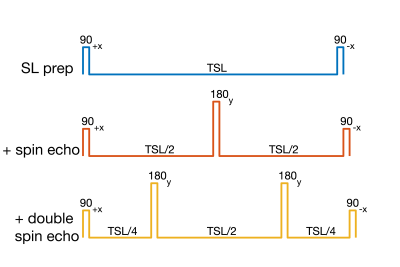
Figure 1: Three example $$$R_{1\rho}$$$ preparation pulses. The traditional spin lock (SL) preparation pulse (top) is known to be sensitive to $$$B_1$$$ and $$$B_0$$$ inhomogeneity. Several studies have suggested $$$B_1$$$ and $$$B_0$$$ insensitive pulses, by including a spin echo (middle) or double spin echo (bottom) as part of the preparation pulse.
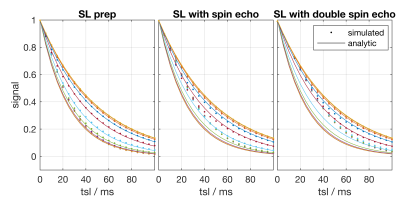
Figure 2: Simulations of $$$R_{1\rho}$$$ dispersion with coupled Bloch equations (dots) compared with the analytic formula for $$$R_{1\rho}$$$ dispersion (lines) over a broad range in spin lock frequency, shown for $$$L$$$=25 $$$\mu$$$m and $$$g$$$=48 mT/m. The simulations and analytic model agree for the traditional spin lock preparation pulse. However, some biases are apparent for the spin echo and double spin echo preparation pulses.
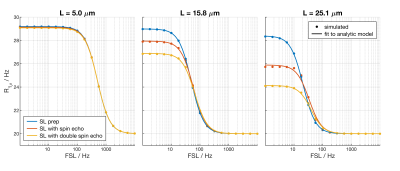
Figure 3: For for small $$$L$$$, $$$R_{1\rho}$$$ dispersion is unaffected by the preparation pulse used, as shown in the left panel. However, as $$$L$$$ increases (or $$$q$$$ decreases), the type of preparation pulse used influences the characteristics of $$$R_{1\rho}$$$ dispersion, most obviously affecting the magnitude of the dispersion estimated. All dispersion curves were fit to the analytic model given in the methods, with the best fit analytic model is shown.
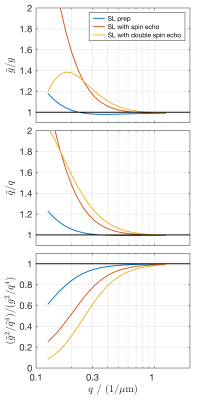
Figure 4: Ratio of estimated (~) vs actual $$$g$$$ and $$$q$$$ used for simulations of $$$R_{1\rho}$$$ dispersion in the diffusion regime. Spin echo and double spin echo SL preparation pulses cause an overestimation of $$$g$$$ (top) and $$$q$$$ (middle). The magnitude of the $$$R_{1\rho}$$$ dispersion goes with $$$g^2/q^4$$$, which is significantly underestimated for small $$$q$$$ (bottom).
DOI: https://doi.org/10.58530/2023/4904