4802
Cartesian Spiral acquisitions for radiotherapy on an MR-Linac1Joint Department of Physics, The Institue of Cancer Research, Sutton, United Kingdom, 2Department of Computing, Imperial College London, London, United Kingdom, 3Department of Radiotherapy, University Medical Center Utrecht, Utrecht, Netherlands
Synopsis
Keywords: Image Reconstruction, Radiotherapy
Respiratory-resolved
4D-MRIs could measure the extent of respiratory motion for online MR-guided
radiotherapy on MR-Linacs. Cartesian spiral (CASPR) trajectories are an
alternative to radial sampling for self-gated 4D-MRIs, because they could avoid
prohibitively long image reconstruction times related to the non-uniform
Fourier Transform. We studied the effect of different sampling parameters on
image quality for CASPR-based sequences on an MR-Linac and reconstructed abdominal
4D-MRI, we found that increasing the number of points per spiral arm improved the
reconstructed image quality, creating a trade-off between spatial and temporal
resolutions.
Introduction
MR-Linacs make it possible to visualise tumours and radiosensitive organs-at-risk while delivering radiation treatment. Online MR-guided radiotherapy can account for anatomical changes between treatment fractions. However, intra-fraction motion such as respiration is not routinely characterised during online imaging and treatment margins are not updated daily, which could limit the radiation dose which can be safely delivered to abdominal cancers. Stereotactic Body Radiation Therapy relies on 4D-CT acquired weeks before treatment to measure respiratory motion amplitudes and calculate margins1.To account for respiration in an online setting, respiratory-resolved 4D-MRIs depicting the abdominal anatomy throughout the respiratory cycle, are required2. While several 4D-MRI reconstruction techniques were developed3, they suffer from long reconstruction times arising from iteratively using the Non-Uniform Fast Fourier Transform in reconstructing non-Cartesian k-space data.
Cartesian sampling, on the other hand, relies on the Fast Fourier Transform during the reconstruction and could offer faster reconstruction time. To enable self-gated 4D-MRI reconstructions, Cartesian spirals (CASPR)4,5 were proposed and have been used in self-gated reconstructions resolving cardiac4 and respiratory motions5, 6. CASPR trajectories rely on “spiral-like” trajectories, which are aligned to a Cartesian grid. Self-gating information can be obtained from the central k-space points of every spiral arm. While a recent work6 demonstrated CASPR-based 4D-MRI on diagnostic MRI scanners, work is needed to adapt CASPR sequences to hybrid MR-Linacs and to identify suitable acquisitions parameters.
Methods
CASPR trajectories based on the Archimedean spiral were simulated using Julia7 to estimate the number of spirals arms required for sufficient coverage of k-space. To avoid rings of unsampled points in k-space, a random component was added to the theoretical regridding. We investigated the effects of the number of samples per spiral arms, the number of turns per spiral arm and the increment between consecutive spiral arms as presented in Figure 1.Based on the simulations, an ultrafast gradient echo CASPR acquisition was implemented on a 1.5T MR-Linac system with 8 coil channels (Unity, Elekta AB, Stockholm) and an abdominal phantom (SUN NUCLEAR Triple Modality 3D Abdominal Phantom) was scanned with different spiral lengths (16, 24, 32, 48 and 64 points per spiral arm), different spiral directions (spiral-out and spiral-in/out on a single arm), and different angle increments between spiral arms (golden angle8 and tiny golden-angle4, 9). Spiral length corresponded to the shot length of the ultrafast gradient echo sequence. From each acquisition, an average volumetric image was reconstructed and compared to a standard Cartesian reference image using Structural Similarity Index.
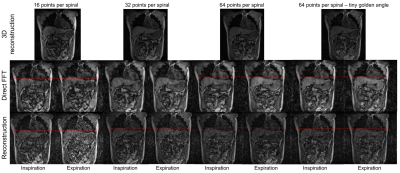
A volunteer was imaged on the MR-Linac, with spiral-out trajectories of different spiral-arm lengths (16, 32, 64 points per spiral arm) with golden-angle increments (Table 1). An extra acquisition with 64 points per spiral-arm with tiny golden-angle increments between consecutive spiral arms was performed. For each acquisition, a volumetric image was reconstructed.
A respiratory self-gating signal was extracted from the central line of k-space and combined across coils using the coil clustering method10, 11. Based on the respiratory signal, each spiral was sorted into one of 6 respiratory bins. After averaging k-space data for points that were sampled more than once in each bin, an iterative compressed-sensing reconstruction11, 12 implemented in Julia has been used to solve the equation:
$$argmin_d \parallel Fd−m \parallel_2^2+ \lambda \parallel TVd\parallel_1$$
with:
- F: Fourier Transform operator
- d: Image
- s: Samples
- λ: Regularisation parameter
- TV: Total-Variation along the respiratory phases
Results
The simulations showed no difference in k-space coverage based on the angle increment (golden-angle and tiny golden-angle). For a given number of profiles (number of spirals × spiral lengths), longer spiral-arms provided a better coverage of k-space (Figure 2).Phantom experiments showed no difference in image quality between the different parameters except for spiral length (Figure 3).
Phantom and volunteer experiments showed RF-noise like artefacts in some coil images. These artefacts however did not appear in the reconstructed average. The intensity of the artefacts decreased with longer spiral length.
Reconstructed volunteer images showed good image quality for 3D-MRI. 4D-MRI had lower SNR, but diaphragm motion could be assessed (Figure 4).
Discussion
The increase in k-space coverage with more densely sampled spiral arms indicates a trade-off between spatial and temporal resolutions. To correctly resolve respiratory motion, a temporal resolution of around 200ms is necessary13, which corresponds to a maximum spiral length of 64 points per spiral for the given sequence parameters.Trajectories could be optimised for a specific resolution to achieve maximal k-space coverage. However, respiratory motion can substantially vary between patients and predicting the sampling for respiratory binned k-space data could be challenging.
Our prototype 4D-MRI reconstruction does not yet fully exploit the full acceleration potential of Cartesian spirals, and 4D-MRI reconstruction for the acquired sequence took 20 minutes. Future work will focus on accelerating the reconstruction for use in online MR-guided radiotherapy workflows through parameter adjustments, software and hardware optimisations.
Conclusion
Self-gated respiratory-resolved 4D-MRIs can be reconstructed from CASPR acquisitions for use in MR-guided radiotherapy on an MR-Linac. We found that longer spiral arms yielded higher image quality for a fixed acquisition time but result in a lower temporal resolution of the respiratory signal.Acknowledgements
This research project was supported by the CRUK Convergence Science Centre at The Institute of Cancer Research, London, and Imperial College London (A26234).
The Institute of Cancer Research and The Royal Marsden NHS Foundation Trust are members of the Elekta MR-Linac Research Consortium.
Philips MR for the source codes and required research licences.
References
1. Kwong, Y., et al., Four-dimensional computed tomography (4DCT): A review of the current status and applications. J Med Imaging Radiat Oncol, 2015. 59(5): p. 545-54.
2. Stemkens, B., E.S. Paulson, and R.H.N. Tijssen, Nuts and bolts of 4D-MRI for radiotherapy. Phys Med Biol, 2018. 63(21): p. 21TR01.
3. Mickevicius, N.J. and E.S. Paulson, Investigation of undersampling and reconstruction algorithm dependence on respiratory correlated 4D-MRI for online MR-guided radiation therapy. Physics in Medicine and Biology, 2017. 62(8): p. 2910-2921.
4. Usman, M., et al., Free breathing whole-heart 3D CINE MRI with self-gated Cartesian trajectory. Magn Reson Imaging, 2017. 38: p. 129-137.
5. Cheng, J.Y., et al., Free-breathing pediatric MRI with nonrigid motion correction and acceleration. Journal of Magnetic Resonance Imaging, 2015. 42(2): p. 407-420.
6. Bruijnen, T., et al. Free-breathing motion compensated 4D (3D+respiration) T2-weighted turbo spin-echo MRI for body imaging. 2022. arXiv:2202.03021.
7. Bezanson, J., et al., Julia: A Fresh Approach to Numerical Computing. SIAM Review, 2017. 59(1): p. 65-98.
8. Feng, L., et al., Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magnetic Resonance in Medicine, 2014. 72(3): p. 707-717.
9. Wundrak, S., et al., Golden ratio sparse MRI using tiny golden angles. Magnetic Resonance in Medicine, 2016. 75(6): p. 2372-2378.
10. Zhang, T., et al., Robust self-navigated body MRI using dense coil arrays. Magnetic Resonance in Medicine, 2016. 76(1): p. 197-205.
11. Feng, L., et al., XD‐GRASP: Golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing. Magnetic Resonance in Medicine, 2016. 75(2): p. 775-788.
12. Lustig, M., D. Donoho, and J.M. Pauly, Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine, 2007. 58(6): p. 1182-1195.
13. Kim, N., et al., MR SIGnature MAtching (MRSIGMA) with retrospective self-evaluation for real-time volumetric motion imaging. Physics in Medicine & Biology, 2021. 66(21): p. 215009.
Figures
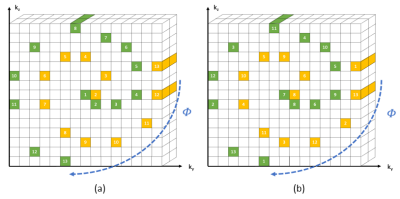
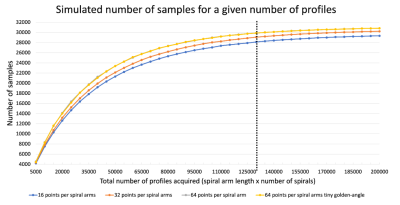
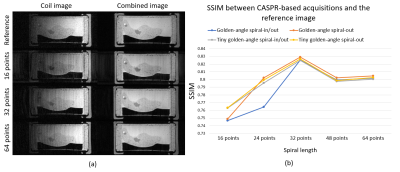
Figure 3: (a) Coil image showing the observed artefact and the coil-combined image. (b) The Structural Similarity Index (SSIM) measured against the reference image is similar between the tested trajectories. SSIM increased up to a spiral arm length of 32 points then remained stable.