4801
Stochastic optimization of 3D non-Cartesian sampling trajectory (SNOPY)1Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States, 2EECS, University of Michigan, Ann Arbor, MI, United States
Synopsis
Keywords: New Trajectories & Spatial Encoding Methods, Machine Learning/Artificial Intelligence
Efficient k-space trajectories are crucial for accelerated MRI. SNOPY proposes a generalized gradient-based method for optimizing 3D non-Cartesian sampling patterns. The algorithm can simultaneously tune multiple properties of sampling patterns, including image quality, hardware constraints (maximum slew rate and gradient strength), reduced peripheral nerve stimulation (PNS), and parameter-weighted contrast. The proposed method applies to various scenarios, such as optimizing gradient waveforms or optimizing rotation angles of radial/spiral trajectories. We adopted several computational strategies to address this non-convex and large-scale problem. Various simulated and in-vivo experiments demonstrated the effectiveness of SNOPY.Introduction
In MRI, efficient sampling strategies can accelerate acquisition and improve image quality. This abstract introduces a data-driven method for automatic trajectory tailoring. SNOPY combines gradient-based and data-driven approaches to learn optimal sampling trajectories from data. SNOPY includes several optimization objectives, including image quality, hardware constraints, PNS suppression, and image contrast. The composite objective enables the simultaneous optimization of multiple characteristics. It is also viable to jointly optimize sampling trajectory with trainable reconstruction algorithms to improve both simultaneously [1]. The algorithm can optimize different attributes of a given sampling trajectory, such as the readout waveform, or the rotation angles of different shots. We introduced several techniques to improve the efficiency of optimization for this large-scale problem. We also tested the proposed methods with multiple imaging applications, including structural and functional imaging. These applications benefited from the SNOPY-optimized sampling trajectories in both simulation and prospective studies.Methods
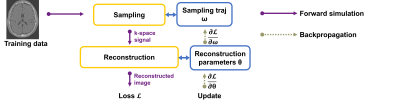
Generally, SNOPY is a machine learning framework that adopts differentiable programming to compute the Jacobian/gradient w.r.t. sampling trajectories required in the gradient-based methods, as shown in Fig 1. SNOPY uses stochastic gradient descent-like algorithms to update sampling trajectories and other parameters, such as the reconstruction weights.The algorithm uses composite optimization objectives to ensure that the optimized sampling trajectories have certain desired properties. The first type of objective is image quality, which encourages images reconstructed from sampled k-space signals to be close to the reference image. The optimization also considers physical constraints, including gradient strength, slew rate, and peripheral nerve stimulation (PNS) effect. We formulated such constraints as soft penalty terms. To maintain certain parameter-weighted contrasts, SNOPY may also include a penalty on the echo time (TE).
Users can optimize various attributes of sampling trajectories via the proposed method. One may optimize existing trajectory parameters, such as rotation angles or (continuous) phase-encoding locations. This approach is easier to implement and compatible with existing reconstruction and correction methods. The second approach, spline-based freeform optimization [1], can directly optimize gradient waveforms. Additionally, it enables multiscale optimization to avoid sub-optimal local minima and further improve optimization results.
SNOPY proposes several techniques for more accurate and efficient optimization. SNOPY uses stochastic gradient Langevin dynamics (SGLD) as the optimizer to accelerate training. One may also pre-calculate the Toeplitz embedding kernel to further reduce memory use [2]. We derived a fast and accurate approximation for Jacobian involving NUFFTs [3]. Without the aforementioned techniques, optimizing 3D trajectories would cost hundreds of GBs of memory. SNOPY enables solving this otherwise prohibitively large problem on a single graphic card (GPU). Table 1 (a) shows the memory efficiency improvement brought by these techniques.
Experiments
We experimented with multiple scenarios to show the broad applicability of the proposed method. Experiment 1 optimized the gradient waveforms initialized by a 3D radial (‘kooshball’) trajectory. Experiment 2 optimized the rotation angles of stack-of-stars trajectories [4]. The third application aims to dampen the PNS effect of rotation EPI (REPI) trajectories [5], which provide an efficient sampling strategy for 3D fMRI at the cost of a high PNS effect.We used two publicly available datasets to optimize the trajectories; both of them contain 3D multi-coil raw k-space data. SKM-TEA (exp. 1) is a 3D quantitative double-echo steady-state (qDESS) knee dataset [6]. The Calgary brain dataset (exp. 2 and 3) is a 3D brain T1w MP-RAGE k-space dataset [7].
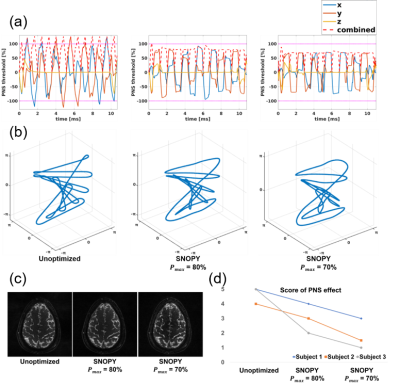
In the prospective studies, we programmed the sampling trajectory with a 3D T1w fat-saturated GRE sequence for experiment 2 using TOPPE [8]. The experiment included 4 healthy subjects. For experiment 3, to rate the PNS effect, we asked 3 participants to score the nerve stimulation with a 5-point Likert scale from ‘mild tingling’ to ‘strong muscular twitch.’ All subjects gave informed consent under local IRB approval.
Results and Discussion
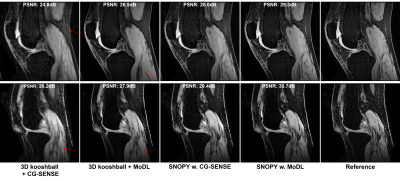
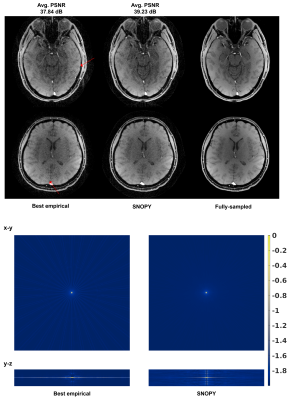
For the spline-based freeform optimization experiment, Table 1 (b) shows the quantitative image quality in the simulation experiment. Across reconstruction methods (CG-SENSE and model-based deep learning, MoDL [9]), SNOPY improved image quality (PSNR) by ~4dB. Fig. 2 shows example slices. Fig. 3 shows the prospective results of experiment 2, optimization of rotational angles of SOS. SNOPY effectively reduced streak artifacts. PSFs of different trajectories also support this finding. Fig 4 displays the PNS effect reduction brought by SNOPY both in simulation studies and patients’ ratings (exp. 3). SNOPY efficiently reduced the severe PNS effect of REPI.In summary, SNOPY provides an effective tool for optimizing 3D non-Cartesian trajectories while satisfying hardware constraints and controlling PNS.
Acknowledgements
This work is supported in part by NIH Grants R01 EB023618 and U01 EB026977, and NSF Grant IIS 1838179.References
[1] Wang, G., Luo, T., Nielsen, J. F., Noll, D. C., & Fessler, J. A. (2022). B-spline parameterized joint optimization of reconstruction and k-space trajectories (BJORK) for accelerated 2d MRI. IEEE Transactions on Medical Imaging, 41(9), 2318-2330.
[2] Fessler, J. A., Lee, S., Olafsson, V. T., Shi, H. R., & Noll, D. C. (2005). Toeplitz-based iterative image reconstruction for MRI with correction for magnetic field inhomogeneity. IEEE Transactions on Signal Processing, 53(9), 3393-3402.
[3] Wang, G., & Fessler, J. A. (2021). Efficient approximation of Jacobian matrices involving a non-uniform fast Fourier transform (NUFFT). arXiv preprint arXiv:2111.02912.
[4] Zhou, Z., Han, F., Yan, L., Wang, D. J., & Hu, P. (2017). Golden‐ratio rotated stack‐of‐stars acquisition for improved volumetric MRI. Magnetic resonance in medicine, 78(6), 2290-2298.
[5] Rettenmeier, C. A., Maziero, D., & Stenger, V. A. (2022). Three dimensional radial echo planar imaging for functional MRI. Magnetic Resonance in Medicine, 87(1), 193-206.
[6] Desai, A. D., Schmidt, A. M., Rubin, E. B., Sandino, C. M., Black, M. S., Mazzoli, V., ... & Chaudhari, A. S. (2022). Skm-tea: A dataset for accelerated mri reconstruction with dense image labels for quantitative clinical evaluation. arXiv preprint arXiv:2203.06823.
[7] Souza, R., Lucena, O., Garrafa, J., Gobbi, D., Saluzzi, M., Appenzeller, S., ... & Lotufo, R. (2018). An open, multi-vendor, multi-field-strength brain MR dataset and analysis of publicly available skull stripping methods agreement. NeuroImage, 170, 482-494.
[8] Nielsen, J. F., & Noll, D. C. (2018). TOPPE: A framework for rapid prototyping of MR pulse sequences. Magnetic resonance in medicine, 79(6), 3128-3134.
[9] Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
[10] Schulte, R. F., & Noeske, R. (2015). Peripheral nerve stimulation‐optimal gradient waveform design. Magnetic resonance in medicine, 74(2), 518-522.
Figures