Synopsis

Keywords: Image Reconstruction, Cardiovascular, Radial Acquisition

Uncertainty quantification (UQ) can provide important information about deep learning algorithms and help interpret the obtained results. UQ for multi-coil dynamic MRI is challenging due to the large scale of the problem and scarce training data. We approach these issues by learning distributions in a lower dimensional latent space using a conditional Wasserstein autoencoder while utilizing the MR data acquisition model and by exploiting spatio-temporal correlations of the cine MR images. Our results indicate excellent image quality accompanied with uncertainty maps that correlate well with estimation errors.

Introduction

Uncertainty quantification (UQ) provides a promising method of characterizing deep learning (DL) algorithms. In 2D dynamic multicoil radial MRI, the lack of large training datasets due to the expensive acquisition process and large-scale of the problem poses major challenges in performing UQ, which involves exploring entire distributions of possible outputs given some input instead of yielding just single estimates. Previous works¹ has demonstrated the usage of Monte Carlo dropout with aleatoric² (MC-Drop+Ale) to accomplish this. However, MC-Drop+Ale assumes Gaussian posterior^2,3 distributions and uncorrelated pixel-wise reconstructions³, which are not necessarily true. To this end, we propose to use a conditional Wasserstein autoencoder (cWAE) that does not impose such assumptions. Here, the distributions are learned in a lower dimensional latent space that requires less computations than in the original image space. The cWAE is a conditional extension of the Wasserstein autoencoder (WAE) framework⁴, that generalizes adversarial autoencoders⁵, and have better sample quality than variational autoencoders⁶. Our work further incorporates the radial acquisition forward model into the network architecture⁷, as well as spatiotemporal⁸ learning, in order to learn efficiently with limited data.

Methods

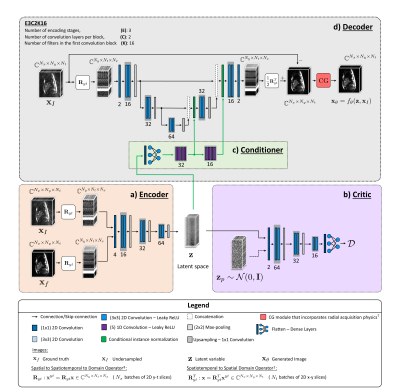
Problem formulation: We denote the complex-valued dynamic MR images reconstructed from fully sampled $$$k$$$-space as $$$\mathbf{x}_{\mathrm{f}}\in\mathbb{C}^{N}=\mathbb{C}^{N_{x}\cdot\,N_{y}\cdot\,N_{t}}$$$. Given the reconstruction $$$\mathbf{x}_{\mathrm{I}}\in\mathbb{C}^{N}$$$ from radially undersampled $$$k$$$-space, our objective is to learn the conditional distribution $$$p(\mathbf{x}_{\mathrm{f}}|\mathbf{x}_{\mathrm{I}})$$$. For this purpose, we consider $$$\mathbf{x}_{\theta}\sim p_{\theta}(\mathbf{x}_{\theta}|\mathbf{x}_{\mathrm{I}})$$$ that are generated by $$$p_{\theta}$$$. Similar to [4], we propose to reformulate Kantorovich's formulation of the optimal transport problem into a conditional autoencoder framework, and define the following objective-
$$W_{\mathrm{cWAE}}(p(\mathbf{x}_{\mathrm{f}}|\mathbf{x}_{\mathrm{I}}),p_{\theta}(\mathbf{x}_{\theta}|\mathbf{x}_{\mathrm{I}}))=\,\underset{q:q_{Z}=p_{Z}}{\displaystyle{\inf}}\,\mathbb{E}_{(\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})\sim\,p(\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})}\mathbb{E}_{\mathbf{z}\sim\,q(\mathbf{z}|\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})}\{c(\mathbf{x}_{\mathrm{f}},f_{\theta}(\mathbf{z},\mathbf{x}_{\mathrm{I}}))\},\tag{1}$$
where $$$c(\cdot,\cdot):\mathbb{C}^{N}\times\mathbb{C}^{N}\rightarrow\mathbb{R}$$$ is a $$$L2$$$ loss in our case, $$$f_{\theta}$$$ is a deterministic function of $$$\mathbf{z}$$$ and $$$\mathbf{x}_{\mathrm{I}}$$$, and $$$q$$$ is the distribution of latent variable $$$\mathbf{z}\sim q(\mathbf{z}|\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})$$$ such that its marginal $$$q_{Z}:=\int q(\mathbf{z}|\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})p(\mathbf{x}_{\mathrm{f}}|\mathbf{x}_{\mathrm{I}})\mathrm{d}\mathbf{x}_{\mathrm{f}}$$$ is identical to $$$p_{z}:=p(\mathbf{z}|\mathbf{x}_{\mathrm{I}})$$$. To allow for a numerically feasible computation (1) is relaxed as-
$$W_{\mathrm{cWAE}}(p(\mathbf{x}_{\mathrm{f}}|\mathbf{x}_{\mathrm{I}}),p_{\theta}(\mathbf{x}_{\mathrm{\theta}}|\mathbf{x}_{\mathrm{I}}))=\,\underset{q}{\displaystyle{\inf}}\,\mathbb{E}_{(\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})\sim\,p(\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})}\mathbb{E}_{\mathbf{z}\sim\,q(\mathbf{z}|\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})}\{c(\mathbf{x}_{\mathrm{f}},f_{\theta}(\mathbf{z},\mathbf{x}_{\mathrm{I}}))\}+\mathcal{D}(q_{Z},p_{Z}),\tag{2}$$
where $$$\mathcal{D}$$$ is any divergence measure in the latent space. Here, the optimal $$$q$$$ that minimizes (2) can be interpreted as an encoder that encodes $$$\mathbf{z}$$$ which is decoded back as $$$\mathbf{x}_{\theta}=f_{\theta}(\mathbf{z},\mathbf{x}_{\mathrm{I}})$$$, provided $$$q_{Z}$$$ is as close as possible to the $$$p_{Z}$$$ with respect to $$$\mathcal{D}$$$.

Implementation: As shown in Fig. 1, XT,YT networks⁸ were used to parameterize a deterministic encoder $$$q(\mathbf{z}|\mathbf{x}_{\mathrm{I}},\mathbf{x}_{\mathrm{f}})$$$, and a deterministic decoder $$$f_{\theta}(\mathbf{z},\mathbf{x}_{\mathrm{I}})$$$. For reconstruction, the decoder utilizes the knowledge encoded in $$$\mathbf{z}$$$ in the form of conditional information through conditional instance normalization⁹ layers with learned parameters. The output $$$f_{\theta}$$$ is equipped with a data-consistency module which incorporates the model of a radial MR data acquisition⁷. As $$$\mathcal{D}$$$, the 1-Wasserstein distance was chosen and a WGAN which provides stable training was implemented¹⁰. In the sense defined by this metric, the WGAN framework tries to ensure that $$$q_{Z}$$$ is as close as possible to the assumed $$$p_{Z}=\mathcal{N}(\mathbf{0},\mathbf{I})$$$. During inference, we only employ the decoder by drawing $$$\mathbf{z}\sim\mathcal{N}(\mathbf{0},\mathbf{I})$$$ given some $$$\mathbf{x}_{\mathrm{I}}$$$, and compute pixel-wise standard deviations of the output samples, which serves as a measure of uncertainty of the reconstruction network.

Dataset: The networks in our study were trained, validated, and tested on data from 11, 4, and 4 subjects, respectively. This individually amounted to 144, 36, and 36 complex-valued cine MRI images with dimensions $$$320\times\,320\times\,30$$$.

Results

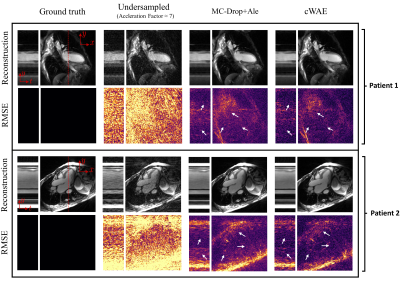
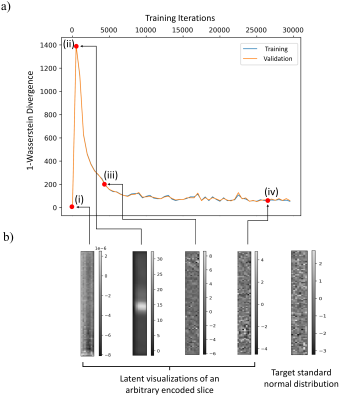
In Fig. 2, we visually compare the reconstruction quality of the cWAE with the MC-Drop+Ale method for two example patient slices. As identified by the white arrows, we see a decrease of RMSE for the proposed cWAE compared to MC-Drop+Ale. Furthermore, Fig. 3 shows that the cWAE has a superior image quality compared to MC-Drop+Ale in terms of NRMSE, PSNR and SSIM¹¹.

By using the WGAN framework to learn $$$p_{Z}=\mathcal{N}(\mathbf{0},\mathbf{I})$$$ in the latent space, as divergence $$$\mathcal{D}$$$ in Fig. 4a decreases with the progression of iterations, Fig. 4b shows that an arbitrary encoded slice starts to resemble a standard normal distribution.

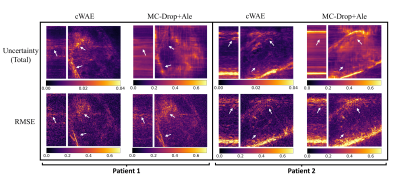
Figure 5 presents a comparison of uncertainty maps generated by the cWAE and MC-Drop+Ale for the same reconstructed slices as in Fig. 2. As can be seen, the uncertainty maps of the cWAE appear sharper than the MC-Drop+Ale, and they correlate well with the corresponding RMSE maps.

Discussion

The dropout rate is also an optimizable variable in the MC-Drop+Ale method^2,3,12, which may cause optimizers to miss information when set too high. Our large-scale problem makes extensive hyper-parameter searches difficult, hence we fixed the dropout rate to 0.2 based on preliminary experiments. Unlike MC-Drop+Ale, cWAE does apply dropouts and utilizes all the learnable parameters to efficiently capture relevant information from the training dataset.

As shown in Fig. 2 and 3, this helps in achieving promising performance without extensive hyper-parameter tuning. Figure 4 illustrates the successful learning of a standard normal distribution in a lower dimensional latent space. This is much more computationally efficient and stable than learning a complex multimodal distribution in the higher-dimensional original image space. Further, based on the strong correlation of uncertainties provided by cWAE with the RMSE in Fig. 5, they can potentially be utilized to improve subsequent post-processing techniques (e.g. segmentation).

Conclusion

Using cWAE, we successfully quantified uncertainties that correlate well with RMSE in a high-dimensional and computationally demanding application of 2D multi-coil dynamic MRI by learning the distribution in smaller latent space while yielding high image quality.

Acknowledgements

We gratefully acknowledge the support of the German Research Foundation, project number GRK2260, BIOQIC.