Synopsis

Keywords: New Trajectories & Spatial Encoding Methods, New Trajectories & Spatial Encoding Methods

The sampling efficiency of radial center-out MRI was increased by using additional oscillating readout gradients, which lead to an accelerated image acquisition. The idea of radial sampling along an oscillating spoke was demonstrated using a clinical MRI system with ultra-fast UTE MRI.

Introduction

Outer k-space regions are highly undersampled in radial MRI compared to the k-space centre. To increase k-space coverage per unit time, different non-Cartesian sampling schemes were proposed such as spiral¹ or rosette² trajectories. However, these trajectories are limited by peripheral nerve stimulation(PNS) and the available slew rate of the gradient systems, and they result in high acoustic noise due to the strong amplitude modulations. To overcome these limitations and improve the sampling efficiency, an additional external gradient can be applied to modulate the k-space trajectory. A previous study showed that PNS becomes independent from the slew rates for frequencies between 10-100kHz³. Recently, a 4^th gradient coil was used to modulate the Cartesian GRE readout to reduce the number of phase encoding steps⁴ using very high slew rates(>5000T/m/s). The idea of using sinusoidal spokes in radial encoding was introduced and compared to linear spokes in numerical phantom simulations⁵.
In this work, we apply an additional Oscillating Readout(OR) to improve the sampling efficiency over a conventional Linear Readout(LR) in radial MRI. Sinusoidal modulations are introduced to spread out the k-space coverage per radial spoke over a k-space sector which allows reducing the number of radial acquisitions. An analytical formulation for acceleration provided by the OR is introduced, the sampling efficiency of the method is characterized via simulations and proof-of-principle phantom measurements were performed.

Methods

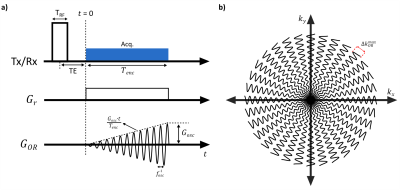
In this study, an OR with gradient $$$G_{OR}$$$, orthogonal to readout gradient $$$G_r$$$, is added such that an entire k-space sector is covered(Fig.1):$$G_{OR}(t)=\frac{G_{osc}\cdot t}{T_{enc}}\text{sin}(2\pi f_{osc}t)$$
Here $$$G_{osc}$$$ is the maximum amplitude of the oscillating gradient at the end of the readout encoding, $$$T_{enc}$$$. To cover the 2D k-space, this modulated encoding is repeated in different directions(Fig.1b). Compared to a LR a full k-space can be sampled faster, as each sector has a finite angular width. The k-space trajectory for $$$G_{OR}(t)$$$ is
$$k_{OR}(t)=\frac{\gamma G_{osc}}{T_{enc}}\int_{0}^{t}t\text{sin}(2\pi f_{osc}t')dt'$$
$$=\frac{\gamma G_{osc}}{T_{enc}}\frac{1}{2\pi f_{osc}}\left[-t\text{cos}(2\pi f_{osc}t)+\frac{1}{2\pi f_{osc}}\text{sin}(2\pi f_{osc}t)\right]$$ for $$$ f_{osc}>0$$$. Assuming $$$T_{enc}=\frac{n}{2f_{osc}}, n \in\mathbb{Z}^+$$$, maximum values of $$$k_{OR}(t)$$$ at the end of encoding is $$$k_{OR}^{max}=k_{OR}(T_{enc})$$$ leading to a sector width of $$\Delta k_{OR}^{max}\approx 2k_{OR}^{max}=\frac{\gamma G_{osc}}{\pi f_{osc}}$$ for $$$f_{osc}\gg 0$$$. For a given 2D FOV, maximum sampling period(Nyquist rate) in LR is $$\Delta k_{LR}^{max}=\frac{1}{FOV}$$
The ratio between $$$\Delta k_{OR}^{max}$$$ and $$$\Delta k_{LR}^{max}$$$ is the acceleration factor, $$$R$$$, of OR over LR: $$R=\frac{\Delta k_{OR}^{max}}{\Delta k_{LR}^{max}}=\text{FOV}\frac{\gamma G_{osc}}{\pi f_{osc}}$$
For a FOV = 128mm, $$$G_{osc}$$$=100mT/m, $$$f_{osc}$$$=20kHz, $$$R$$$ is 8.7. For a given FOV and frequency(e.g.,20kHz), R can be set by adjusting $$$G_{osc}$$$. $$$G_{osc}$$$ is limited not only by hardware requirements but also by SNR, which is intrinsically proportional to $$$\sqrt{T_{enc}}$$$.
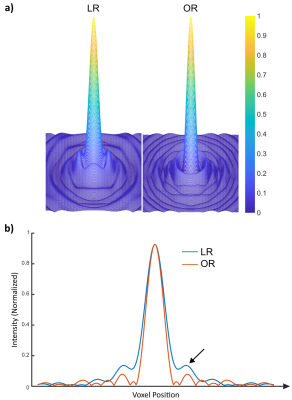
To assess the performance Bloch simulations of a numerical phantom were conducted. For a FOV=(128mm)³, matrix-size=256x256, $$$G_r$$$=20mT/m, TR=1.3ms, and $$$\sqrt{T_{enc}}$$$=1.2ms, number of spokes ($$$N_s$$$=1024, 128, and 64) were simulated using LR($$$G_{osc}$$$=0) and OR($$$G_{osc}$$$=100mT/m, $$$ f_{osc}$$$=20kHz, $$$R$$$=8.7, Oversampling factor=16). The PSF of each technique was calculated for $$$N_s$$$=64, corresponding to 25.1x/2.9x undersampling for LR/OR. In addition, RMSE of the simulated images were compared.
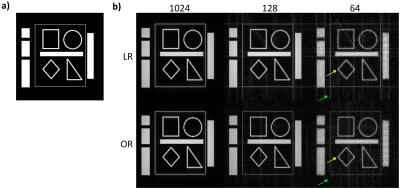
A planar(4-mm-thick) phantom(10g/L agar-agar, 1g/L CuSO4) was prepared(Fig.2a), and a UTE sequence with the modulated trajectory was used to acquire images at a clinical MRI system(Prisma-Fit,Siemens). The data was undersampled retrospectively to demonstrate the performance for different $$$R$$$ values. Oscillations in the readout were realized by the system gradients: $$$G_{osc}$$$=0 and 10mT/m, $$$f_{osc}$$$=1kHz, and $$$R$$$=17.3. The gradient waveforms were monitored using field probes⁶. The edge sharpness of the images was quantified⁷.

Results

In Fig.3, the PSF of LR and OR are presented. The Full-Width-Half-Maximum(FWHM) of the PSF of OR was 13.8% narrower and the highest side lobe of the PSF of OR(black arrow) was 35% smaller compared to LR. In Fig.4b, simulations of the numerical phantom are shown. Images calculated with OR have reduced streaking(green arrows) and distortion(yellow arrows) artifacts compared to conventional radial imaging. RMSE of the images with respect to the ideal image(Fig.4a) simulated with LR/OR with $$$R$$$=8.7 was 4.7/4.2, 42.1/35.8, and 54.0/45.1, for 1024, 128, and 64 spokes, respectively, corresponding to 11%, 18%, and 19% relative improvements.
In Fig.2b, phantom images are compared for LR and OR. The use of OR substantially reduced the streaking(green arrows) and distortion(blue arrows) artefacts. The edge sharpness was improved by 38% using OR at $$$R$$$=17.3. For 128 spokes, coherent artefacts(red arrow) were observed on the OR images.
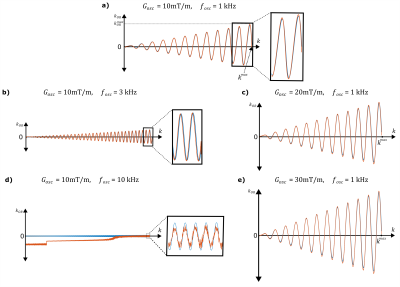
In Fig.5, the ideal and measured k-space trajectories are shown for various oscillation frequencies and amplitudes. Until $$$f_{osc}$$$=10kHz, the waveforms were accurate using the system gradients.

Discussion

The proposed method was also tested on a planar external gradient coil⁸ driven simultaneously with the linear system gradients. Due to limited gradient power amplifier performance, the measurements were conducted with ultra-low bandwidth acquisition, which resulted in strong susceptibility artefacts.
Despite reduced streaking and distortion artefacts, the OR images still showed coherent artefacts that could not be removed with iterative reconstruction. Artifacts could be reduced by modulating the amplitude and frequency of the oscillating gradients randomly⁹.

Conclusion

In this work, we propose an oscillating readout which may in future operate at inaudible frequency to accelerate the radial imaging. Addition of oscillating gradients improved the edge sharpness by 35%. Simulations showed a substantial increase in the image quality by reducing streaking artifacts and decreasing mean squared error.

Acknowledgements

.

References

(1) Ahn, C.; Kim, J.; Cho, Z. High-Speed Spiral-Scan Echo Planar NMR Imaging-I. IEEE Trans. Med. Imaging 1986, 5 (1), 2–7. https://doi.org/10.1109/TMI.1986.4307732.

(2) Likes, R. S. Moving Gradient Zeugmatography, 1981.

(3) Saritas, E. U.; Goodwill, P. W.; Zhang, G. Z.; Conolly, S. M. Magnetostimulation Limits in Magnetic Particle Imaging. IEEE Trans. Med. Imaging 2013, 32 (9), 1600–1610. https://doi.org/10.1109/TMI.2013.2260764.

(4) Versteeg, E.; Klomp, D. W.; Siero, J. C. A Silent Gradient Axis for Soundless Spatial Encoding to Enable Fast and Quiet Brain Imaging. Magn. Reson. Med. 2022, 87 (2), 1062–1073. https://doi.org/10.1002/mrm.29010.

(5) Ahmad, R.; Potter, L. C.; Kuppusamy, P. Oscillating Radial Trajectories for Reduced Undersampling Artifacts. In Proc. Intl. Soc. Mag. Reson. Med. 17; 2009.

(6) Wehkamp, N.; Rovedo, P.; Fischer, E.; Hennig, J.; Zaitsev, M. Frequency-Adjustable Magnetic Field Probes. Magn. Reson. Med. 2021, 85 (2), 1123–1133.

(7) Ilbey, S.; Jung, M.; Emir, U.; Bock, M.; Özen, A. C. Characterizing Off-Center MRI with ZTE. Z Med Phys 2022, early access. https://doi.org/10.1016/j.zemedi.2022.09.002.

(8) Littin, S.; Gallichan, D.; Welz, A. M.; Jia, F.; Dewdney, A.; Weber, H.; Schultz, G.; Hennig, J.; Zaitsev, M. Monoplanar Gradient System for Imaging with Nonlinear Gradients. Magn. Reson. Mater. Phys. Biol. Med. 2015, 28 (5), 447–457. https://doi.org/10.1007/s10334-015-0481-8.

(9) Bilgin, A.; Trouard, T. P.; Gmitro, A. F.; Altbach, M. I. Randomly Perturbed Radial Trajectories for Compressed Sensing MRI. In Proc. Intl. Soc. Mag. Reson. Med. 16; 2008.