Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Existing deep learning-based methods for MR reconstruction mainly use MSE as loss function to train the network under the assumption that MR images follow the sub-Gaussian distribution, without considering the real distribution of the images. In this work, we propose a new DL-based method that models the image distribution with equilibrium Langevin dynamic to converge the distribution, and trains the network with Wasserstein distance to approach the real distribution. Experimental results on highly undersampled MR data demonstrate the superior performance of the proposed method.

Introduction

Deep learning (DL) has been an import tool in image reconstruction and shown great potential in significantly speeding up MR imaging^1,2. Most DL-based methods for MR reconstruction use the mean square error (MSE) of the reconstructed image and the ground truth to train the network model, which assumes that the MR images follow the sub-Gaussian distribution. However, in practice, the distribution of the MR images is more complicated than Gaussian distribution. In this work, we propose a novel reconstruction approach that uses the Langevin dynamics to model the distribution of MR images. We adopt the deep equilibrium model to converge the distribution, and use the Wasserstein distance to measure the distance between the converged distribution and the real distribution.

Theory

Langevin dynamics can be used to generate samples from the posterior³, which can be formulated as follows in MR imaging:$$x_{t+1}\leftarrow x_{t}+\eta _{t}\bigtriangledown_{x_{t}}log\mu (x_{t}|y)+\sqrt{2\eta _{t}}\zeta _{t}, \zeta _{t}\sim N(0,1) (1)$$ where $$$x\in \mathbb{C}^{N}$$$is the vector of pixels we wish to reconstruct from the k-space data $$$y\in \mathbb{C}^{M}$$$, $$$\mu (x|y)$$$ is the posterior probability, $$$\eta$$$ is the step size, $$$t$$$ is the time point corresponding to iteration number.
The core problem in Eq.(1) is to compute the posterior probability $$$log\mu (x|y)$$$. Assuming the imaging noise is the i.i.d. Gaussian noise, $$$log\mu (y|x)=-\left\| Ax-y\right\|_{2}^{2}$$$, according to Bayes’ rule, $$$log\mu (x|y)=-\left\| Ax-y\right\|_{2}^{2}+R(x)$$$, where $$$R(x)$$$ represents the imaging prior. Therefore, Eq.(1) follows$$x_{t+1}= x_{t}+\eta _{t}\bigtriangledown (R(x_{t})-\left\| Ax-y\right\|_{2}^{2})+\sqrt{2\eta _{t}}\zeta _{t}=x_{t}-\eta _{t}A^H (Ax-y)+\eta _{t}\bigtriangledown R(x_{t})+\sqrt{2\eta _{t}}\zeta _{t} (2)$$ Eq.(2) is the form of noisy gradient descent, similar to the gradient descent algorithm. Recalling to the unrolling methods, deep network is used to approximate the unknown functions in the imaging model with end-to-end training. Thus, we replace the function $$$\bigtriangledown R(x_{t})$$$ with a parameterized operator $$$g(x)$$$.
To make the image distribution converge, we adopt the deep equilibrium model (DEQ)⁴. In DEQ, the mapping $$$f_{\theta }$$$, corresponding to the iteration that $$$x_{t+1}=f_{\theta }(x_{t};y)$$$, has the same parameters in each iteration. The limit of $$$x_{T}$$$ as $$$T\to \infty $$$, provided it exists, is a fixed point of the operator $$$f_{\theta }(\cdot ;y)$$$. The fixed-point $$$x_{T}$$$ is a good estimate of the image given its measurement $$$y$$$.
With DEQ and end-to-end Langevin dynamics, the reconstructed image distribution converges. We also use the network architecture of WGAN with gradient penalty⁵ to make the converged distribution approach to the real distribution.

Method

T2-weighted MR data from MoDL was used to evaluate the feasibility of the proposed method. The raw data were acquired using a 3D T2 CUBE sequence with 12-channel head coil. 360 slices from training subjects were used to train the model and 164 slices from the test subject for testing. Variable density psedo-random sampling mask was used to demonstrate the performance of reconstruction methods.

Results

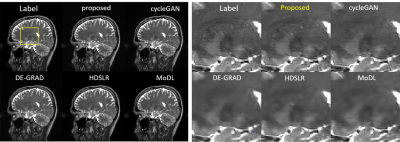
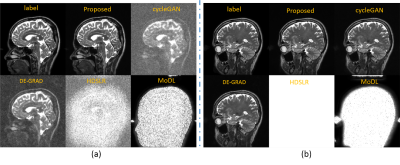
We compared our proposed approach with different DL-based MR reconstruction methods, including cycleGAN⁶, DE-GRAD⁷, HDSLR⁸ and MoDL⁹.
The qualitative comparisons with an acceleration factor of 12 are shown in Fig 1. The reconstructed images, as well as the corresponding zoom-in images were provided. The data distribution modeling methods (proposed and cycleGAN) achieve better performance than the conventional data sample modeling methods (DE-GRAD, HDSLR and MoDL) due to the advantage of data distribution modeling. The proposed method can faithfully reconstruct the images with clearer anatomical details indicated by the zoom-in images. Quantitative results of different methods with R=12 are presented in Table I. results reported are on the entire test dataset, thus the values in the table are the mean values. Figure 2 shows the robustness of the proposed method when changing the data settings. Specifically, we directly changed the input of the trained model to random noise, and added 5dB noise to the measurement. Figure 2(a) illustrates the reconstructions with noise input, and Fig 2(b) is the reconstructions with noisy measurement. Unrolling-based methods (HDSLR and MoDL) failed to reconstruct images, and the proposed method achieves good performance in detail preservation and artifact removal, showing better robustness.

Conclusion

In this work, we have proposed a novel DL-based method to approximate the real distribution of MR images. Experimental results show the superior performance of the proposed approach.

Acknowledgements

This work was supported in part by the National Key Research and Development Program of China under Grant 2020YFA0712200; in part by the National Natural Science Foundation of China under Grants 12026603, U1805261 and 62106252; in part by the Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province under Grant 2020B1212060051.