Synopsis

Keywords: Image Reconstruction, Data Processing, Image Reconstruction, Unsupervised Learning, Deep Image Prior

We propose an unsupervised learning method for dynamic MRI reconstruction. Our method, Deep Image prior with StruCtUred Sparsity (DISCUS), is an extension of Deep Image Prior (DIP) and employs joint optimization of network parameters and latent code vectors to recover image series. We enforce group sparsity on code vectors to reveal the underlying low-dimensional manifold of the image series. Using two sets of in vivo measurements and digital phantom simulation, we show that our approach significantly improves the reconstruction quality in terms of Normalized Mean Square Error (NMSE) and Structure Similarity Index Measure (SSIM) compared to compressed sensing and DIP.

Introduction

Supervised deep learning methods require a large corpus of fully sampled training data for image reconstruction. However, these methods may not be suitable for many dynamic MRI applications where acquiring fully sampled k-space is not feasible. Among recently proposed unsupervised methods, Deep Image Prior (DIP) has received significant attention; it utilizes the network structure as a prior¹. More recent extensions of DIP recover a series of images using manifold learning^2,3. However, these methods rely on the assumption that temporal closeness (order of acquisition) is tied to the similarity of generated images, which is not the case for many applications such as perfusion and Late Gadolinium Enhancement (LGE). In addition, these methods require defining the dimensionality of the hidden manifold explicitly, which may not be known a priori. In this work, we propose an extension of DIP for image series recovery that exploits the common support of sparse latent code vectors without any assumption on the manifold structure or dimensionality, making this method suitable for a wide range of MRI applications.

Methods

To recover image series $$$\{\boldsymbol{x}_t\}_{t=1}^T$$$ with $$$T$$$ frames from given undersampled measurements $$$\{\boldsymbol{y}_t\}_{t=1}^T$$$, the proposed method, Deep Image prior with StruCtUred Sparsity (DISCUS), solves the following optimization problem:
$$\hat{\boldsymbol{z}}_0, \hat{\boldsymbol{z}}_t, \hat{\boldsymbol{\theta}} = \DeclareMathOperator*{\argmin}{arg\,min} \argmin_{\boldsymbol{z}_0, \boldsymbol{z}_t, \boldsymbol{\theta}} {\sum_{t=1}^{T}{\left\| \boldsymbol{A}_t\boldsymbol{G}_{\boldsymbol{\theta}}(\boldsymbol{z}_0, \boldsymbol{z}_t)-\boldsymbol{y}_t \right\|_2^2}+\lambda\left\| \boldsymbol{z}_{:}\right\|_{2,1}}\label{eq:discus}\hspace{2cm}(1)$$
where $$$\boldsymbol{y}_t\in\mathbb{C}^M$$$ is the measured k-space for the $$$t^\text{th}$$$ frame, $$$\boldsymbol{x}_t\in\mathbb{C}^N$$$ is an $$$N$$$-pixel image, $$$\boldsymbol{z}_0\in\mathbb{R}^{kN}$$$ with user-defined $$$k>0$$$, $$$\boldsymbol{z}_t\in\mathbb{R}^N$$$, $$$\left\| \boldsymbol{z}_{:}\right\|_{2,1} = {\sum_{n=1}^N\sqrt{\sum_{t} z_t^2[n]}}$$$, $$$\lambda>0$$$ is a constant, $$$\boldsymbol{A}_t\in\mathbb{C}^{M\times N}$$$ is the known forward operator, and $$$\hat{\boldsymbol{x}}_t = \boldsymbol{G}_{\hat{\boldsymbol{\theta}}}(\hat{\boldsymbol{z}}_0, \hat{\boldsymbol{z}}_t)$$$ is the image generated from a neural network, $$$\boldsymbol{G}_{\boldsymbol{\theta}}$$$, parameterized by $$$\boldsymbol{\theta}$$$. The code vector $$$\boldsymbol{z}_0$$$ is kept common across all images, while the code vector $$$\boldsymbol{z}_t$$$ is specific to the $$$t^\text{th}$$$ image. Both $$$\boldsymbol{z}_0$$$ and $$$\boldsymbol{z}_t$$$ are fed into the generator, $$$\boldsymbol{G}_{\boldsymbol{\theta}}$$$, as input channels. The generator maps these code vectors to an estimate of $$$\boldsymbol{x}_t$$$. The second term in Eq. 1 represents a hybrid $$$\ell_2$$$-$$$\ell_1$$$ norm that promotes group sparsity⁴ and encourages all code vectors to have a support that is not only sparse but also common across all $$$T$$$ code vectors; this support represents the dimensionality of the underlying manifold. Note, we do not explicitly constraint the dimensionality of the manifold or impose a smoothness constraint on the temporal evolution of the generated images.
To assess the performance of DISCUS, we simulated a $$$64\times64$$$ Shepp-Logan phantom with random rotation between $$$-4^\circ$$$ and $$$+4^\circ$$$ to generate $$$T=32$$$ images. The simulated data was undersampled at $$$R=2$$$ in k-space to generate $$$\{\boldsymbol{y}_t\}_{t=1}^T$$$. To further evaluate DISCUS on data from human subjects, we collected two $$$128\times128$$$ T1-weighted free-breathing single-shot image series ($$$T=16$$$) using LGE-PSIR sequence without contrast on a 3T scanner (MAGETOM Vida, Siemens Healthcare, Erlangen, Germany); one series was collected in the long axis (HLA) view, and the other was collected in the short axis (SAX) view. The multi-coil data were converted to single-coil data using ESPIRiT maps⁵ and retrospectively downsampled at $$$R=2$$$ to generate $$$\{\boldsymbol{y}_t\}_{t=1}^T$$$. The generator implementation was based on a U-Net architecture with six convolutional layers. DISCUS was compared to traditional sparsity-based compressed sensing (CS-L1) and the traditional DIP¹, where each frame in the series was recovered separately.

Results

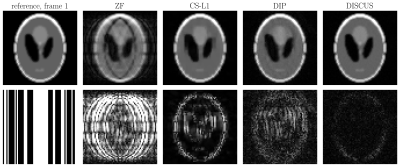
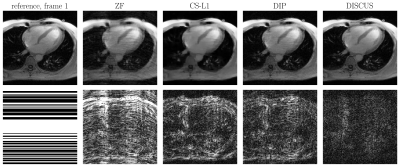
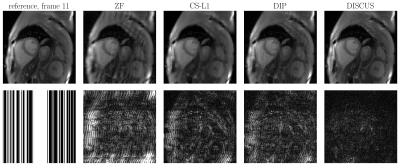
Table 1 shows the NMSE (in dB) and SSIM values for CS-L1, DIP, and the proposed DISCUS method for the three datasets. The values reported are an average over 32 frames for the phantom and 16 frames for HLA and SAX. In Figs. 1-3, the first column shows the reference frame (top) and the corresponding k-space sampling mask (bottom), and the next columns show reconstructed images (top) and corresponding error maps (bottom) of typical frames from these datasets.

Discussion

Our method outperforms CS-L1 and DIP by a considerable margin in terms of NSME (Table 1). DISCUS also outperforms other methods in terms of SSIM for HLA and SAX datasets. For the phantom dataset, CS-L1 shows higher SSIM, which can be attributed to the piece-wise constant nature of the Shepp-Logan phantom being well-suited for the sparsity based prior used in CS-L1. We also found that increasing the number of frames in series further improves NMSE and SSIM because more data facilitates manifold learning (data not shown). Figs. 1-3 indicate that DISCUS yields high quality reconstruction with visibly diminished artifacts. Interestingly, the number of non-zero entries, $$$m$$$, in each member of $$$\{\boldsymbol{z}_t\}_{t=1}^T$$$ for phantom, HLA, and SAX datasets was 1, 7 and 3, respectively. For phantom, $$$m=1$$$ correctly identifies the dimensionality of the underlying manifold (rotation) to be one. For HLA and SAX, one would expect a one-dimensional manifold originating from the respiratory motion. For HLA, $$$m=7$$$ can be attributed to sources of variation other than the respiratory motion, including timing of the RF pulses and beat-to-beat variations. Attempts to find a lower-dimensional manifold by forcing $$$m<7$$$ during the training resulted in worse NMSE and SSIM values (data not shown), which highlights the challenge of prescribing a manifold with predetermined dimensionality. In future, we will extend this work on multicoil MRI and a larger dataset.

Conclusion

By encouraging sparsity and common support among latent code vectors, we extend DIP to jointly recover an image series.

Acknowledgements

This work was funded by NIH projects R01HL148103, R01EB029957 and R01HL151697.