Synopsis

Keywords: Parallel Imaging, Data Acquisition, Brain reconstruction, Cardiac reconstruction

We present a U-Net based deep learning model to estimate the multi-channel ESPIRiT maps directly from uniformly-undersampled multi-channel multi-slice MR data. The model is trained with a hybrid loss function using fully-sampled multi-slice axial brain datasets from the same MR receiving coil system. The proposed model robustly predicted ESPIRiT maps from uniformly-undersampled k-space brain and cardiac MR data, yielding highly comparable performance to reconstruction using to acquired reference ESPIRiT maps. Our proposed method presents a general strategy for calibrationless parallel imaging reconstruction through learning from coil and protocol specific data.

Introduction

Most existing methods for parallel image reconstruction in image, k-space or hybrid space require coil sensitivity calibration data either from additional pre-scan or autocalibration signals. Often there exists inconsistency between calibration data and undersampled data, e.g., due to motions, causing artifacts in the reconstructed images^1,2. ESPIRiT³ is an effective hybrid-space reconstruction method. It utilizes k-space kernel operations to derive a set of eigenvector maps, i.e., ESPIRiT maps, to effectively represent coil sensitivity information. We present a deep learning model to estimate the multi-channel ESPIRiT maps directly from uniformly-undersampled multi-channel multi-slice MR data. The model is trained using fully-sampled multi-slice axial brain datasets from the same MR receiving coil system.

Methods

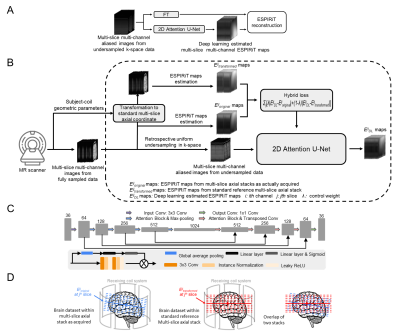
Specifically, a deep learning model is developed for mapping aliased images to the corresponding ESPIRiT maps (Figure 1). The input of the model is the multi-channel aliased MR images from uniformly-undersampled multi-channel data, while the output is the corresponding multi-channel ESPIRiT maps. An attention U-Net model^4-6 is adopted (Figure 1C).

The coil sensitivity information in any MRI system is largely coil-specific. When scanning a particular subject in the clinical MRI setting, the exact coil sensitivity profiles or ESPIRiT maps within any imaging slice also depend on the orientation/position of the slice with respect to MR receiving coil system (Figure 1D). Such subject-coil geometry information is available during the scan and recorded in the DICOM header. We incorporate such information by imposing a hybrid loss function. Specifically, the model is trained by minimizing a hybrid L1 loss on two sets of multi-slice multi-channel ESPIRiT maps in the following Equation (1). $$ argmin_{\theta} \sum_{ij} [\lambda |E^{ij}_{DL}-E^{ij}_{original}|+(1-\lambda)|E^{ij}_{DL}-E^{ij}_{transformed}|] $$ Here λ is a learnable parameter to control the loss contributions. Specifically, E^ij_original and E^ij_transformed represent two ESPIRiT maps for the ith channel at the jth slice within their original multi-slice locations and their transformed locations within the standard reference multi-slice axial stack (Figure 1D, respectively. This reference stack has a fixed orientation and position relative to the magnet and gradient coil center. Its orientation and position typically have a fixed geometric relation to the coil system. Thus E^ij_transformed should be mostly coil specific and dataset independent. Meanwhile, E^ij_original will be dataset dependent since each multi-slice axial head scan can be prescribed with a slightly different geometry. In practice, E^ij_transformed and E^ij_original differ from each other in position and orientation but will be very similar to a certain extent due to their geometric proximity and the spatial smoothness nature of ESPIRiT maps. Therefore, incorporating E^ij_transformed as part of the loss function will indirectly facilitate the learning process through improving stabilization and convergency.

The training and testing data were from the publicly available Calgary-Campinas MR brain database⁷. They included 65 fully-sampled human brain datasets from 65 individual healthy subjects that were acquired on a 1.5T clinical GE scanner. To further evaluate the robustness of the proposed method, cardiac MRI data from OCMR public database⁸ were also used. Adam optimizer⁹ was carried out for training with β1 = 0.9, β2 = 0.999 and initial learning rate = 0.0001. λ was initialized to 0.5 and gradually decreased to zero during training. The training was conducted on a Geforce RTX 3090 GPU using PyTorch 1.8.1 package¹⁰ with a batch size of 32 and 100 epochs. The total training time was approximately 27.8 hrs and 7.4 hrs, respectively for the brain 6-channel model and the cardiac 6-channel model. For evaluation, we compared the deep learning results with these using the reference maps derived from 24 consecutive central k-space lines.

Results

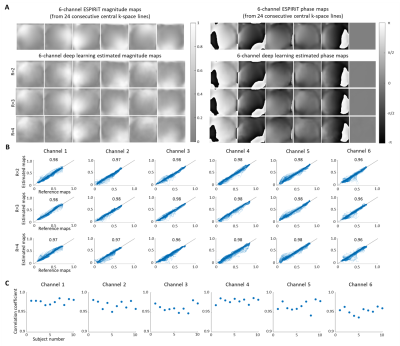
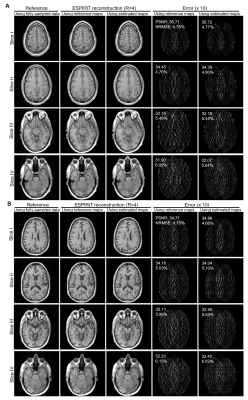
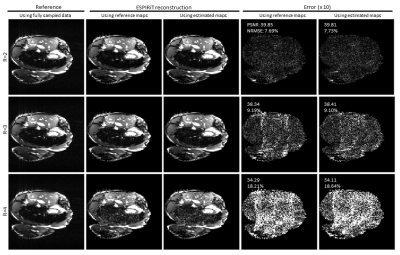
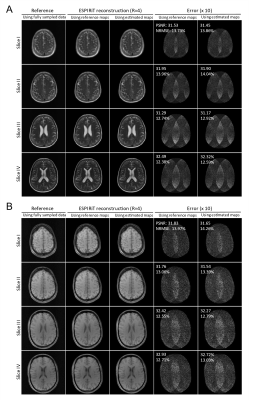
Figure 2 shows the typical results of deep learning estimated ESPIRiT maps. Quantitatively, there existed a high degree of pixel-wise correlation between the deep learning estimated and reference ESPIRiT magnitude maps, indicating the robustness of the proposed deep learning estimation of ESPIRiT maps. Figure 3 presents the results at R = 4 for two subjects with large roll rotation and large overall translation, respectively, again showing similar performance at all slice locations. Figure 4 shows the cardiac results, again demonstrating comparable performance to that using reference maps. These results demonstrated that our method could adapt to the reconstruction of cardiac data, where there are often signal voids and relatively more rapid coil sensitivity variations when compared to brain data.

Discussion and Conclusions

The proposed deep learning model is capable of robustly predicting multi-channel ESPIRiT maps from uniformly-undersampled k-space data even at high acceleration. The model training and application are coil specific. However, this may not pose a severe restriction as we envision that, in an era of data-driven computing, truly effective MRI scanners should move towards self-learning, i.e., constant performance improvement through learning from the data generated by itself. Note that the multi-contrast model can be also trained on data from fastMRI¹¹, as shown in Figure 5. In summary, our proposed framework offers a general strategy for calibrationless parallel imaging reconstruction through learning from coil and protocol specific data. It is highly applicable to application scenarios where accurate coil sensitivity calibration is difficult.