Synopsis

Keywords: Parallel Imaging, Image Reconstruction

We propose an iterative reconstruction method of parallel imaging using convolutional neural network (CNN)-based denoising in the image domain and data-consistency processing in k-space. The proposed method reduces the noise and artifacts of a reconstructed image compared with the iterative method using sparsity of wavelet transform, suggesting that using CNN-based denoising in iterative reconstruction is effective in reducing noise in parallel imaging.

Introduction

The signal-to-noise ratio of an image reconstructed by parallel imaging (PI) decreases as the reduction factor increases because of the noise enhancement in the reconstruction process. To reduce the noise in PI, several methods have been proposed to remove noise using sparse representation method in iterative parallel imaging reconstruction.^1,2 However, the noise cannot be sufficiently removed in the case of high reduction factor because some of the true signal components in the sparse representation cannot be separated from the enhanced noise. Convolutional neural network (CNN)-based denoising methods^3,4 are expected to reduce noise more precisely than sparsity-based methods by using the statistical features of the image. In this study, we propose an iterative reconstruction method of parallel imaging for reducing noise at a high reduction factor by using CNN-based denoising in the image domain in the iterative reconstruction of PI.

Method

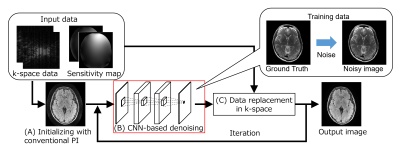
Figure 1 shows the processing flow of the proposed method. (A) An initial combined image is reconstructed from the under-sampled k-space data and sensitivity map. (B) CNN-based denoising is applied to the combined image. The CNN is trained using the datasets of ground-truth and noisy images, where the noisy images are created by adding complex Gaussian noise to the ground-truth images. (C) By multiplying the sensitivity map and applying Fourier transform, denoised multi-channel k-space data are calculated, and the data in the measured point in k-space are replaced with the acquired data for data consistency. A PI method for the fulfilled k-space is then applied to create a combined image for output. The input image of step (B) is replaced with the combine image to repeat steps (B) and (C) until the output image converges. A three-layer CNN is used in step (B). The CNN is trained with 40516 patches of 32×32 pixels extracted from 3 brain images (T1 weighted, T2 weighted, and fluid attenuated inversion recovery (FLAIR) image) and 3 knee images (Proton density weighted, T2 weighted, and T2* weighted image) of a volunteer by using a 3T magnetic resonance imaging (MRI) scanner (FUJIFILM Healthcare Corp., Japan). We conducted an evaluation of the proposed method. We first obtained a brain image of a FLAIR sequence from a healthy volunteer using a 1.5 Tesla MRI scanner and 8-channel head coil (FUJIFILM Healthcare Corp., Japan). The k-space data of the slice was retrospectively under-sampled by an equispaced pattern with reduction factor (R) = 3 and 4. Images were reconstructed with the conventional PI method, iterative reconstruction method with wavelet transform and soft-thresholding (iterative WT-ST method), and proposed method (iterative CNN method). Image quality was assessed by calculating the root-mean-square error (RMSE) between each image and the image reconstructed without under-sampling. This study was approved by the ethics committee of FUJIFILM Healthcare Corporation. All data used in this study were obtained after receipt of written informed consent.

Results

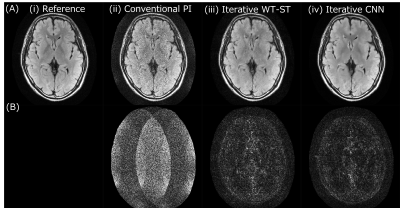
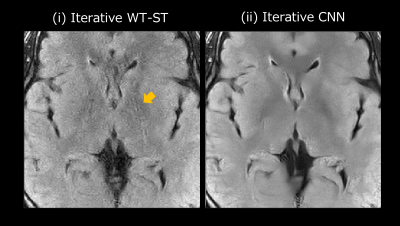
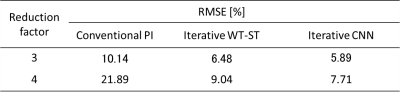
Figure 2 shows the images reconstructed with each method with R = 4. The image from the conventional PI method (ii) had large noise and differences from the reference image, especially in the central region. Although the iterative WT-ST method reduced noise throughout its image compared with the conventional PI, the iterative CNN method reduced noise more than the iterative WT-ST method. Figure 3 shows the expanded images of the iterative WT-ST and iterative CNN methods with R = 4. In addition to reducing noise, the iterative CNN method reduced artifacts in its image compared with that of the iterative WT-ST method (yellow arrow). Table 1 shows RMSE of each method with R = 3 and 4. Under both conditions, the iterative CNN method showed a lower RMSE than the conventional PI and iterative WT-ST methods. Compared with the iterative WT-ST method, RMSE was reduced by 9 and 15% in R = 3 and 4, respectively, with the iterative CNN method compared with the iterative WT-ST method.

Discussions

In conventional PI, noise increases because of the geometry-factor, especially in the central region. The iterative WT-ST method reduces noise by using the sparsity of the reconstructed image in the wavelet domain. However, because some of the true signal components cannot be separated from noise, reconstruction errors consisting of remaining noise, blur, and artifacts become large with a higher R, which increases noise. CNN-based denoising separates signal and noise components more precisely on the basis of the statistical features of the image, so the error in reconstruction is smaller than with the iterative WT-ST method. The proposed iterative CNN method successfully reduced noise with both R = 3 and 4. This suggests that robustness to R can be achieved without using the under-sampling pattern in k-space or under-sampled data in the training step of CNN denoising.

Conclusion

We proposed an iterative reconstruction method of PI using CNN-based denoising in the image domain and data-consistency processing in k-space. The proposed method reduced the noise and artifacts of a reconstructed image compared with the iterative WT-ST method, suggesting that using CNN-based denoising in iterative reconstruction reduces reconstruction errors in PI.

Acknowledgements

No acknowledgement found.