4744
Can machine learning resolve model degeneracy in tissue microstructure estimation?1Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2AINOSTICS Ltd., Manchester, United Kingdom
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Machine Learning/Artificial Intelligence
This work investigates the impact of model degeneracy on machine learning-based tissue microstructure estimation. While there have been several empirical reports suggesting machine learning can not resolve model degeneracy, the impact of model degeneracy is poorly understood. Here we show how model degeneracy can be categorised into three types with varying degrees of impact on machine learning-based microstructure estimation. Our finding is important for designing optimal training data distribution.Introduction
In this study we assess the impact diffusion MRI (dMRI) model degeneracy has on machine learning (ML) estimation of tissue microstructure parameters. Microstructure imaging exploits biophysical models to relate microstructural tissue features to dMRI signals via biologically-meaningful parameters1,2. Traditionally, the estimation of these parameters involves iteratively minimizing a non-convex objective function, a procedure which is slow and does not guarantee convergence. Parameter estimation is further complicated by intrinsic dMRI signal model degeneracy3: different parameter combinations minimizing the same objective function.ML has been shown to both accelerate parameter estimation and reduce its imaging protocol requirements4,5. However, the effect model degeneracy has on ML methods remains poorly understood. While there are growing empirical evidence demonstrating ML approaches remain susceptible to the aforementioned degeneracy issues6-8, it remains unclear to what extent this is true in general, or under what mechanism degeneracy impacts ML methods. This work aims to address this by investigating the effect the degeneracy has on ML supervised parameter estimation.
Theory
In this section we derive the ML output when a degenerate subset of samples is included during training. ML maps an input dMRI signal vector $$$x\in \mathbb{R}^m$$$ to its corresponding output microstructure parameter vector $$$y\in \mathbb{R}^k$$$ via a parametric function $$$f_{\theta}$$$. Given a set of P exemplar vector pairs $$$\{ x_p, y_p\}$$$, p=1,…,N, the ML function parameters $$$\theta$$$ are adjusted to approximate the required mapping. Training algorithms generally minimize the mean squared error (MSE) between network output and target:$$ E_{\theta} = \frac{1}{N}\sum_{p=1}^{N} [f_{\theta}(x_p) -y_p]^2 $$
Importantly, for any given input vector generates only one output vector; this function can only represent one-to-one or many-to-one mappings. Degenerate, multivalued mappings cannot be represented9.
Without loss of generality, we will assume the degenerate subset of samples is the first n samples of the training set. For this subset, each sample has a distinct microstructure parameter vector but predicts the same signal:
$$ \forall i,j\in \{ 1,2,...,n\}\Rightarrow x_i=x_j, y_i\neq y_j $$
The network MSE can be decomposed as:
$$ E_{\theta} = \frac{1}{N}\sum_{p=1}^{n} [f_{\theta}(x_q) -y_p]^2 + \frac{1}{N}\sum_{p=n+1}^{N} [f_{\theta}(x_p) -y_p]^2 $$
with $$$q\in \{ 1,2,...,n\}$$$. If we assume the network is flexible enough to minimize each of the two MSE terms independently, the trained network will directly minimize the degenerate subset contribution to the loss:
$$ \frac{\partial E_{\theta}}{\partial f_{\theta}(x_q)}=0=\frac{2}{N}\sum_{p=1}^{n} [f_{\theta}(x_q) -y_p]=\frac{2}{N}nf_{\theta}(x_p)-\frac{2}{N}\sum_{p=1}^{n}y_p $$
Hence:
$$ f_{\theta}(x_q)=\frac{\sum_{p=1}^{n}y_p }{n} $$
Degeneracy observed during training thus leads to averaging over that degeneracy during inference.
The impact of this result depends on the nature of the degeneracy that can be broadly classified into three categories: (1) degeneracy that genuinely obscures biological differences, i.e. different underlying parameters give rise to the same signal; (2) degeneracy that potentially obscures biological differences, but only one non-degenerate case is observed in real data; (3) degeneracy that corresponds to no biological differences. This work explores the impact of these three categories degeneracy on ML parameter estimation.
Materials and Methods
ML framework and biophysical modelWe use a multi-layer perceptron as a representative example of ML frameworks. We used revised-NODDI2,10-12 to represent the biophysical models.
Experiments
We design two experiments to assess the impact of degeneracy types 2 and 3 on ML in the context of selecting training data. We hypothesize that ML can partially resolve type 2 degeneracy by excluding the degenerate cases that are not observed in real data from the training set. We compare the performance of estimating revised-NODDI parameters from single-shell data, using a uniform training distribution which includes all degenerate parameter combinations and an in vivo derived training distribution which includes only typical real data combinations.
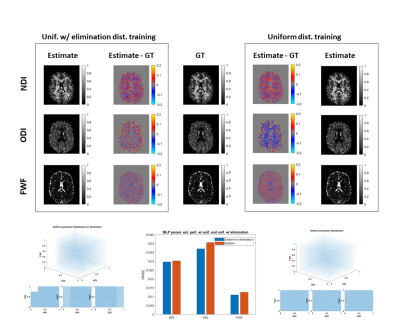
Further, we hypothesize that the presence of type 3 degeneracy in the training set, although being irrelevant for the degenerate parameter estimation, may indirectly compromise training samples without degeneracy. We thus compare the performance of estimating revised-NODDI parameters from multi-shell data, using a uniform training distribution which includes type 3 degeneracy and the same distribution from which the degeneracy has been partially eliminated.
Results and discussions
The analytical derivation in the theory section shows that ML cannot resolve type 1 degeneracy, as the ML function is trained to predict the mean of the training sample; this has been observed empirically7. A similar result has been recently derived describing the influence of noise on ML-derived parameter estimation13.Figure 1 shows estimation performance is improved by excluding type 2, biologically reasonable but not empirically-observed, parameter combinations from the training data. We note that this may lead to issues in the presence of genuinely abnormal parameter combinations, for example in pathology.
Figure 2 shows performance is improved by partially excluding type 3, non-biologically realistic, degenerate parameter combinations from the training data. Even though these parameter combinations are not encountered at inference, including them during training negatively impacts performance in the adjacent regions of genuine biological parameter space we do care about.
Together, these results call into question recent recommendations to use uniform training distributions8; overall ML parameter estimation performance may be improved by carefully choosing training data that excludes type 2 and type 3 degeneracy.
Acknowledgements
Computing resources and support were provided by AINOSTICS Ltd., enabled through funding by Innovate UK.References
1. Alexander, D.C., et al., Imaging brain microstructure with diffusion MRI: practicality and applications. NMR Biomed, 2019. 32(4): p. e3841.
2. Zhang, H., et al., NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 2012. 61(4): p. 1000-16.
3. Jelescu, I.O., et al., Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed, 2016. 29(1): p. 33-47.
4. Golkov, V., et al., q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Trans Med Imaging, 2016. 35(5): p. 1344-1351.
5. Palombo, M., et al., SANDI: A compartment -based model for non-invasive apparent soma and neurite imaging by diffusion MRI. Neuroimage, 2020. 215: p. 116835.
6. de Almeida Martins, J.P., et al., Neural networks for parameter estimation in microstructural MRI: Application to a diffusion-relaxation model of white matter. Neuroimage, 2021. 244: p. 118601.
7. Reisert, M., et al., Disentangling micro from mesostructure by diffusion MRI: A Bayesian approach. Neuroimage, 2017. 147: p. 964-975.
8. Gyori, N., et al. In-vivo neural soma imaging using b-tensor encoding and deep learning. in Proceedings of the 27th Annual Meeting of ISMRM, Montreal, Canada. 2019.
9. Bishop, C.M. and C.M. Roach, Fast curve fitting using neural networks. J Review of scientific instruments, 1992. 63(10): p. 4450-4456.
10. Guerreri, M., et al., Revised NODDI model for diffusion MRI data with multiple b-tensor encodings, in International Society for Magnetic Resonance in Medicine. 2018: Paris, France.
11. Guerreri, M., et al., Tortuosity assumption not the cause of NODDI’s incompatibility with tensor-valued diffusion encoding, in International Society for Magnetic Resonance in Medicine. 2020: Virtual conference.
12. Guerreri, M., et al., Quantifying tissue microstructural changes associated with short-term learning using model-based diffusion MRI, in International Society for Magnetic Resonance in Medicine. 2021.
13. Coelho, S., E. Fieremans, and D.S. Novikov. How do we know we measure tissue parameters, not the prior? in International Society of Magnetic Resonance in Medicine. 2021.
Figures
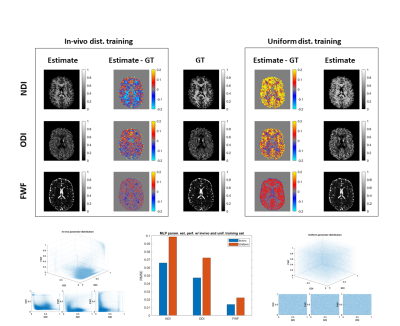
Figure 1: comparing estimation performance of NODDI parameter maps from single-shell data via deep learning using in-vivo (left) and uniform (right) training distributions. We assess the estimated neurite density index (NDI), orientation dispersion index (ODI) and free water fraction (FWF) parameter maps against the ground truth (GT) values. The in-vivo training distribution provides better performance than uniform distribution for all parameters suggesting that by eliminating degeneracy from the training set, machine learning can partially resolve degeneracy issues.