4740
Accelerating DCE-MRI Analysis for Prostate Cancer Diagnosis with Deep Neural Networks1Department of Radiological Sciences, University of California, Los Angeles, Los Angeles, CA, United States
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Data Analysis, dynamic contrast enhanced
A deep learning based DCE-MRI analysis method was proposed with a dedicated neural network architecture and data generation framework. The proposed method does not need DCE-MRI data acquisition or annotation for training. Compared to conventional non-linear least square (NLLS) fitting methods, the proposed method significantly reduced the average processing time from hours to few minutes while preserved the estimation quality.Purpose
This study aimed at providing a deep learning-based method for dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) analysis for prostate cancer (PCa) diagnosis. Conventional methods for DCE analysis rely on the time-consuming non-linear least square (NLLS) fitting of a tracer-kinetic model. We proposed a deep leaning-based method that directly predicts vascular parameters from the DCE-MRI data. We also proposed a data generation framework to generate training data for model training. Consequently, our method does not require data acquisition or annotation during training. Experimental results reveal that we reduced the average processing time of a study from hours to less than two minutes while preserving the estimation quality.Introduction
Prostate cancer (PCa) is the most common solid organ malignant tumor and the second learning cause of cancer-related death in men in the US1. DCE-MRI is a clinically useful and non-invasive technique to quantify tumor vasculature and tumor perfusion characteristics2,3. Prostate DCE-MRI acquires a time series of T1-weighted images before, during, and after the injection of a contrast agent (CA). After data acquisition, DCE-MRI analysis is performed on the time-series of T1-weighted images to investigate temporal changes of CA in vessels and tissues. Conventionally, the non-linear least squares (NLLS) fitting is used for tracer-kinetic modeling of DCE data4,5,6. However, despite promising results, NLLS suffers from long processing times (several hours for a study) and noisy parameter maps due to the non-convexity of the cost function.Several recent studies have demonstrated the advantages of using deep learning in DCE-MRI analysis for cancer diagnoses 7,8,9. Nalepa et. al. proposed to use supervised learning to directly estimate parameter maps for brain tumor diagnosis7. Witowski et. al. proposed a supervised method using 3D CNN for breast DCE-MRI[8]. Prostate DCE-MRI has much more timesteps (10 times more) than breast DCE-MRI and the prostate MR images are often not as well aligned as brain MR images, making it hard to collect enough data and annotations for supervised learning. Ottens et. al. proposed an unsupervised method for pancreatic DCE-MRI analysis9. Although their method does not need annotations, their model training relies on acquired DCE-MRI data. Besides, their model architecture and loss functions are proved to be suboptimal.
In this paper, we propose a Transformer10-based neural network (NN) that directly estimates vascular parameters from data without any data acquisition and annotation. The proposed method can reduce the computational footprint of DCE-MRI analysis and improve its practical utilization.
Method
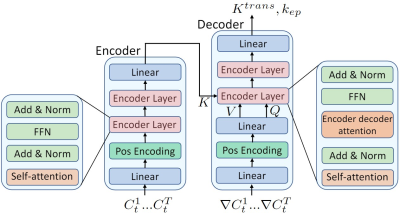
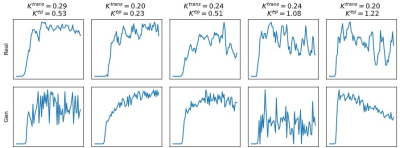
In total, 30 patients with whole-mount histopathology (WMHP) confirmed PCa were included. DCE-MRI data are time series of T1-weighted images acquired from Siemens MR machines. The architecture of the proposed method was illustrated in Fig.1. The network takes the time-series data and its gradient as input, and outputs the vascular parameter $$$K^{trans}$$$ and $$$k_{ep}$$$. We first generated training data using the Tofts’ model11. In Tofts’ model, the blood concentration of contrast agent (CA) $$$C_t(t)$$$ is formulated as the convolution of arterial input function (AIF) and impulse response of the tissue: $$C_t(t) = \int_0^t C_p(\tau)\delta(t-\tau) d\tau$$ The impulse response $$\delta(t) = K^{trans}\exp(-k_{ep}t)$$ is controlled by vascular parameters $$$K^{trans}$$$ and $$$k_{ep}$$$ that reflects the permeability and dispersion characteristics of the blood tissue interaction. To generate training data, we randomly sampled $$$K^{trans}$$$ and $$$k_{ep}$$$ and then synthesized time-series data using Tofts’ model. The Parker12 AIF was used in our experiments. To imitate the noise in real data, we added Gaussian noise to the generated data. Some examples of generated data and real data were shown in Fig.2. Then, we trained our neural network with generated data. We designed a transformer-based neural network that takes both the time-series data and its gradient as input because the gradient of the time-series provides additional information about the data structure. During testing, the time-series data were input into the trained network to get the predicted parameters. Then, we performed ten steps of NLLS fitting to further refine the results.Results
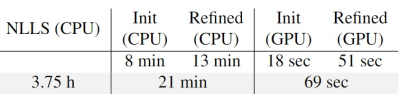
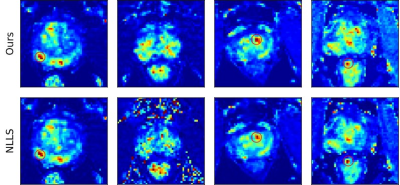
We compared our method with the conventional non-linear least square (NLLS) fitting method. Our method achieved more accurate parameter estimation while reducing the processing time from more than 3 hours to only few minutes. Fig.3 summarizes the processing time of NLLS and our method on different devices. Some example $$$K^{trans}$$$ maps are shown in Fig.4 and red circles indicate tumors. We quantitatively compared the reconstruction error of our method and NLLS. The reconstruction error quantized by the L1 distance between the input time-series $$$C_t$$$ and the reconstructed time-series $$$\hat{C}_t$$$ using predicted parameters and Tofts’ model. Results in Fig.5 demonstrate that- the proposed gradient-enhanced transformer outperforms the plain transformer.
- our method achieves lower reconstruction error compared to NLLS.
Discussions
Both qualitative $$$K^{trans}$$$ maps in Fig.4 and quantitative comparisons in Fig.5 demonstrate that our method produced more accurate parameter estimation and significantly reduced the processing time.Conclusions
In conclusion, we introduced a deep learning-based method for DCE-MRI analysis with 1) a specifically designed network architecture and 2) a data generation framework for model training. We showed the proposed method significantly reduced the computational time of prostate DCE-MRI analysis and improved the accuracy of parameter estimation compared to the conventional NLLS-based method. We believe our method greatly improved the practical utilization of DCE-MRI in prostate cancer diagnosis.Acknowledgements
This work was supported in part by the National Institutes of Health R01-CA248506 and funds from the Integrated Diagnostics Program, Departments of Radiological Sciences and Pathology, David Geffen School of Medicine, UCLA.References
[1] Siegel, Rebecca L., et al. "Cancer statistics, 2019." CA: a cancer journal for clinicians 69.1 (2019): 7-34.
[2] Hara, Noboru, et al. "Dynamic contrast‐enhanced magnetic resonance imaging (DCE‐MRI) is a useful modality for the precise detection and staging of early prostate cancer." The Prostate 62.2 (2005): 140-147.
[3] Kim, Jeong Kon, et al. "Wash‐in rate on the basis of dynamic contrast‐enhanced MRI: usefulness for prostate cancer detection and localization." Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine 22.5 (2005): 639-646.
[4] Bonekamp, David, and Katarzyna J. Macura. "Dynamic contrast-enhanced magnetic resonance imaging in the evaluation of the prostate." Topics in Magnetic Resonance Imaging 19.6 (2008): 273-284.
[5] Sung, Kyunghyun. "Modified MR dispersion imaging in prostate dynamic contrast‐enhanced MRI." Journal of Magnetic Resonance Imaging 50.4 (2019): 1307-1317.
[6] Verma, Sadhna, et al. "Overview of dynamic contrast-enhanced MRI in prostate cancer diagnosis and management." AJR. American journal of roentgenology 198.6 (2012): 1277.
[7] Nalepa, Jakub, et al. "Fully-automated deep learning-powered system for DCE-MRI analysis of brain tumors." Artificial intelligence in medicine 102 (2020): 101769.
[8] Ottens, Tim, et al. "Deep learning DCE-MRI parameter estimation: application in pancreatic cancer." Medical Image Analysis (2022): 102512.
[9] Witowski, Jan, et al. "Improving breast cancer diagnostics with deep learning for MRI." Science Translational Medicine 14.664 (2022): eabo4802.
[10] Vaswani, Ashish, et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
[11] Tofts, Paul S., et al. "Estimating kinetic parameters from dynamic contrast‐enhanced T1‐weighted MRI of a diffusable tracer: standardized quantities and symbols." Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine 10.3 (1999): 223-232.
[12] Parker, Geoff JM, et al. "Experimentally‐derived functional form for a population‐averaged high‐temporal‐resolution arterial input function for dynamic contrast‐enhanced MRI." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 56.5 (2006): 993-1000.
Figures