Introduction

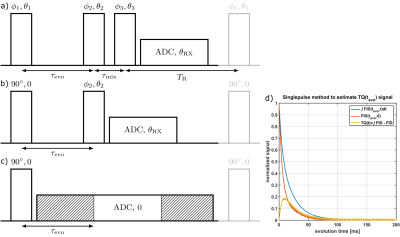
The sodium triple quantum (TQ) signal is a potential biomarker for cell viability^1,2. However, complicated multi-pulse phase cycling sequences, like the TQTPPI³ sequence, have long measurement times for the sodium TQ-signal. This limits the application of the TQ-signal for clinical imaging.

The typical TQ filtering (TQF) sequence^1,3-5 as shown in Fig.1 creates the T₃₁-coherences, which contain all the relevant information about the environment of the sodium nucleus, directly after the first pulse by the transition $$$T_{31}\rightarrow{}T_{11}$$$. However, it is impossible to directly detect the T₃₁-coherences⁶. To measure the $$$T_{31}$$$-signal, a second RF pulse is used to create $$$T_{33}$$$-TQ coherences. Application of a sophisticated phase cycling scheme allows extracting the T₃₃ coherences. The third RF pulse is converting T₃₃ to T₃₁ coherences, which in the presence of quadrupole interaction is evolving to observable T₁₁ coherences. The low signal and phase cycling scheme result in a long measurement time of the sodium TQ-signal.

This study investigates the possibility to extract information for T₃₁ coherences directly following the first RF-pulse. We compare our data with theory and with the state-of-the-art results from fixed TQTPPI sequence^3,7. Moreover, we discuss this method under ideal and realistic conditions.

Materials and Methods

Imagine a single excitation pulse followed by a varying evolution period $$$\tau_{evo}$$$ and a subsequent readout window as shown in Fig.1. The ²³Na signal contains T₁₁-coherences with amplitude and T₃₁-coherences which are observed indirectly with amplitude . The resulting FID can be described by:
$$FID(\tau_{evo},t)=A_{SQ}(\tau_{evo})f_{11}^{(1)}(t)+A_{TQ}(\tau_{evo})f_{13}^{(1)}(t),$$ where $$f_{11}^{(1)}(t)=A_s\exp(-t/T_{2s})+A_f\exp(-t/T_{2f})$$
and $$f_{13}^{(1)}(t)=\frac{\sqrt{6}}{5}(\exp(-t/T_{2s})-\exp(-t/T_{2f}))\;[1]$$ are the transition functions for T₁₁ coherences and evolution $$$T_{31}\rightarrow{}T_{11}$$$, respectively. A_s=0.4 and A_f=0.6 are the theoretical amplitudes of the long and short component with relaxation times T_2s and T_2f, respectively. By using one extended readout window and removing all points prior to $$$\tau_{evo}$$$ for every $$$\tau_{evo}$$$-step, all evolution periods are combined in one readout.

Now we still need to extract the $$$T_{31}$$$-signal from the acquired FID. For this, we use the fact that the integral of a Lorentzian function (Fourier transform (FT) of a one-sided exponential function), is independent of the width of the curve:
$$\int_{-\infty}^{\infty}\frac{T_2}{1+T_2^2\omega^2}d\omega=\pi$$
The TQ-signal consist of a difference of two exponentials [1] and therefore the integral over its FT vanishes, while integral over the SQ signal is proportional to its amplitude A_SQ. Consequently, the resulting integral only consists of the SQ-signal. The integral over the FID however contains both signals. The TQ-signal then is calculated by subtracting both normalized integrals for every $$$\tau_{evo}$$$-step
$$A_{TQ}(\tau_{evo})=\frac{\int{}FID(\tau_{evo},t)dt}{\int{}FID(0,t)dt}-\frac{\int{}FT(FID(\tau_{evo},t))dt}{\int{}FT(FID(0,t))dt}$$
Note, that for mono-exponential decay, both integrals are proportional to A_SQ and with normalization the difference vanishes as expected. To obtain the T₃₁ evolution curve $$$f_{13}^{(1)}(t)$$$ from this, we need a normalization factor that removes the influence of the relaxation times and amplitudes:
$$Norm=\frac{\int{}SQdt}{\int{}TQdt}=\frac{A_sT_{2s}+A_fT_{2f}}{\frac{\sqrt{6}}{5}(T_{2s}-T_{2f})}$$

Measurement data was acquired at a 9.4T preclinical MRI (Bruker Biospec 94/20) using a linear ¹H/²³Na Bruker volume coil. The samples contained 154mM NaCl and [2,4,6]% w/w agar. The single-pulse sequence parameters were: flip angle 90°, repetition time TR=500ms, number of averages N_A=64, number of FID points N_FID=4096 and length of acquisition window t_acq=410ms. Number of $$$\tau_{evo}$$$-points was set to 2048 with $$$\tau_{evo,max}=205ms$$$.Total acquisition duration of the single-pulse sequence was 32s per sample.

For comparison, we used the fixed-$$$\tau_{evo}$$$ TQTPPI^3,7 with 26 different $$$\tau_{evo}$$$ times in the range of 0.1ms to 120ms. Total acquisition duration of the TQTPPI sequence was approximately 3h per sample.

Results/Discussion

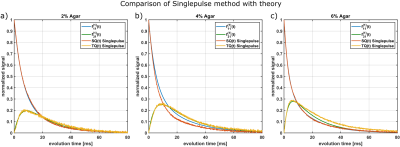
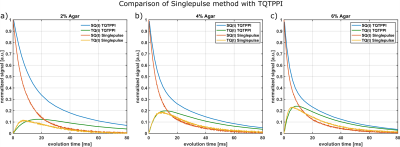
Fig.2 compares this method with the theoretical $$$f_{13}^{(1)}(\tau_{evo})$$$ using T_2s and T_2f from a bi-exponential fit of the FID. For all samples, the maximum of single-pulse TQ signal and the maximum of $$$f_{13}^{(1)}(\tau_{evo})$$$ are in close agreement. The TQ signal of the 6% agar decays slower than $$$f_{13}^{(1)}(\tau_{evo})$$$ for larger $$$\tau_{evo}$$$, which indicates that the FID is not bi-exponential due to B₀ inhomogeneities. The SQ amplitudes deviate from the theoretical values and therefore the FID deviates slightly from $$$f_{11}^{(1)}(\tau_{evo})$$$ for the 4% agar sample. This was also reported in literature ^8,9. The relaxation times, however, are the same.

Fig.3 compares the single-pulse method with the TQTPPI sequence. The maximum of the TQ-signals approximately coincide between both methods for all samples. However, the relaxation times deviate substantially. The single-pulse FID decays with the T₂* times while the TQTPPI FID decays with the T₂ times. This is the result of the 180° pulse in the TQTPPI sequence, which refocuses signal loss due to B₀ inhomogeneities.

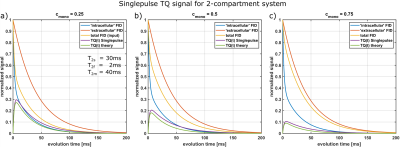
For multi-compartment systems, the integrals are more complicated. We considered the case of a bi-exponential (“intracellular”) and mono-exponential (“extracellular”) compartment and a resulting tri-exponential decay. As Fig.4 shows, the resulting TQ-signal from the single-pulse method only slightly overestimates the TQ signal expected from the system. An in-vivo investigation remains necessary to account for more complex relaxation behavior in biological tissue.

Conclusion

This study presents a new method to estimate the ²³Na TQ signal by only using a single-pulse sequence. With this method, the TQ measurement duration can be dramatically reduced in comparison to TQ pulse sequences. Combination of the method with a multi-echo imaging sequence will enable TQ estimation in-vivo with the SQ time efficiency.

Acknowledgements

A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida.