4642
Effect of regularization parameter on model-based deep learning framework for accelerated MRI
Sampada Bhave1, Saurav Sajib1, Aniket Pramanik2, Mathews Jacob2, and Samir Sharma1
1Canon Medical Research USA Inc, Mayfield, OH, United States, 2University of Iowa, Iowa City, IA, United States
1Canon Medical Research USA Inc, Mayfield, OH, United States, 2University of Iowa, Iowa City, IA, United States
Synopsis
Keywords: Image Reconstruction, Image Reconstruction
Model-based deep learning algorithms offer high quality reconstructions for accelerated acquisitions. Training the regularization parameter λ can lead to instabilities during training. In this work, we evaluated effect of fixing λ parameter while training. We observed no difference in image quality when the network was trained with a fixed λ parameter when the fixed value was equal to the value learned from training. We observed that IQ is dependent on the fixed λ values used during training. Furthermore, we observed that tuning the λ parameter during inference adapts the framework to the SNR of the testing dataset, yielding improved performance.Introduction
Model-based deep-learning algorithms have shown great promise in reconstructing accelerated MRI acquisitions1,2. These algorithms alternate between the neural network denoiser and the data consistency blocks. The regularization parameter λ balances the relative contribution of these two blocks to the reconstructed image. When this parameter is trained, we have observed some instabilities (Fig.1), similar to a previous report3. One way to mitigate this problem is to use a fixed λ value during training. However, fixing this parameter can lead to a decrease in performance as it may not be the optimal value. In this work, we evaluate the effect of fixing the λ value during training on the reconstructed image quality (IQ). We also evaluate the effect of varying this parameter during inference as a way to compensate for fixing it during training.Methods
MoDL Framework: For this study, we used the MoDL algorithm2. The under-sampled MRI acquisition can be modelled as $$$b = A(x) + n$$$, where $$$b$$$ is the undersampled data, $$$A$$$ is the forward operator which incorporates coil sensitivities, sampling mask and Fourier transform and $$$n$$$ is white Gaussian noise. MoDL framework is formulated as follows2:$$argmin_x \frac{λ}{2} ‖A(x)-b‖_2^2 + ‖N_w (x)‖_2^2$$
where the first term is the data-consistency term and the second term is the deep-learning-based denoiser. Here $$$N$$$ is the learned CNN that depends on learned parameters $$$w$$$.
Data Acquisition: T1, T2, and FLAIR data were acquired on human subjects on Vantage Orian 1.5T and Vantage Galan 3T systems (Canon Medical Systems Corporation, Tochigi, Japan) using a 16-channel head/neck and 32-channel head coil. All the datasets were acquired with informed consent and IRB approval.
Experiments: A total of 3000 2D datasets were used for training, and 700 datasets were used for testing. The training data was generated by undersampling the fully-sampled dataset with a variable-density sampling pattern with an acceleration factor of 4. A single complex CNN network was trained for both 1.5T and 3T data with a complex-MSE loss function and Adam optimizer. At first, MoDL was trained with a learnable l value. Then, MoDL was trained with a fixed l value. We evaluated the performance of MoDL for different fixed λ values. The network was trained with a fixed l value equal to the trained lambda (TL) value, for TL/2, and TL*2. In total, four different networks were trained: 1) λ is trainable, 2) λ is fixed and equal to trained λ, 3) λ is fixed and equal to TL/2, and 4) λ is fixed and equal to TL*2. Additionally, the λ value was also varied at inference for each of the four trained networks. The different inference λ values were TL, 2*TL, and TL/2. PSNR and SSIM metrics were used to analyze IQ.
Results
We observed that the network with λ as a trainable parameter and the network with fixed λ equal to trained λ have similar performance both quantitatively (PSNR: 39.27 and 39.20 respectively, SSIM: 0.95 for both) and qualitatively as seen in Fig2a-b (first two rows) and Fig.3 respectively. Fig.4 shows the IQ from networks trained with different fixed λ values for 1.5T(top row) and 3T(bottom row) datasets. We observed that the network yielded similar performance for different λ values for low SNR(1.5T). However, for high SNR datasets, artifacts were observed in the network with training lambda = TL/2. IQ improved with the increase in λ value. Within the range of lambda values in this study, inference λ value higher than that used in training yielded sharper images (Fig.5a) for 3T datasets. This is also reflected in higher SSIM and PSNR values (Fig.2c-d). In contrast, for 1.5T datasets, the inference λ equal to λ during training gave the best performance. Higher inference λ resulted in noise amplification (Fig.5b) leading to a decrease in PSNR (Fig.2c).Discussion
The network performance is not affected when the λ parameter is fixed when the fixed value was equal to the value learned from training, thus mitigating the concerns from the instabilities when the parameter is trained. The networks with different fixed λ parameters yield different image quality. To address this issue, a few networks with different fixed λ parameters can be trained to find the optimal value. Some of the IQ degradation due to fixing the λ during training can be compensated by tuning the λ during inference. When the SNR of the testing data is low, higher weighting needs to be given to the ML denoiser, whereas when the SNR of the testing data is high, higher weighting given to the data-consistency term gives optimal results. Thus, tuning the λ parameter at inference can improve performance for a specific acquisition thereby offering flexibility to train a single network for different acquisition settings.Conclusion
In this work, we evaluated the effect of using a fixed λ parameter during training. We also demonstrated that tuning this parameter during inference to adapt to the SNR of the testing dataset can further improve performance.Acknowledgements
No acknowledgement found.References
[1] Sun, Jian, Huibin Li, and Zongben Xu. "Deep ADMM-Net for compressive sensing MRI." Advances in neural information processing systems 29 (2016).
[2] Aggarwal, Hemant K., Merry P. Mani, and Mathews Jacob. "MoDL: Model-based deep learning architecture for inverse problems." IEEE transactions on medical imaging 38.2 (2018): 394-405.
[3] Hammernik, Kerstin, et al. "Systematic evaluation of iterative deep neural networks for fast parallel MRI reconstruction with sensitivity‐weighted coil combination." Magnetic Resonance in Medicine 86.4 (2021): 1859-1872.
Figures
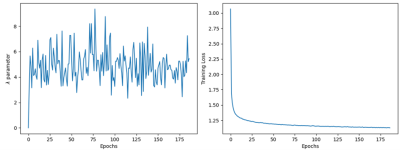
Figure 1: Plot of λ parameter
vs epoch for the network where the λ parameter is trained (left plot). We
observe a large variance in the λ parameter value throughout the epochs even as
the training converges (right plot).
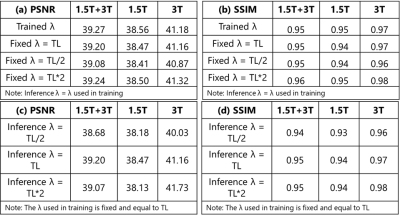
Figure 2: Quantitative comparison for
network performance with different λ values used during training and
inference for combined 3T and 1.5T, 3T only, and 1.5T only datasets: (a) and (b)
show the PSNR and SSIM for different λ
values used during training. (c) and (d) show PSNR and SSIM when the λ value is changed during inference.
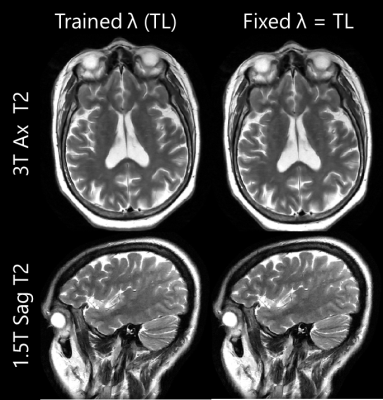
Figure 3: IQ comparison of reconstructions
from the network with fixed λ = trained λ
for 3T (top row) and 1.5T (bottom row) datasets. IQ was very similar for both
networks.
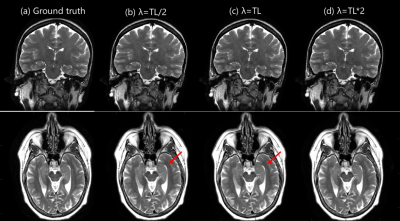
Figure 4: Qualitative comparison of network
performance with different λ values: The reconstruction from
networks trained with fixed λ value equal to trained lambda
(TL)/2, trained lambda (TL), and trained lambda (TL)*2 shown in (b-d)
respectively are compared to ground truth shown in (a). We observed that the
reconstructions have very similar image quality for low SNR 1.5T (top row). Some
IQ degradation (red arrows) is seen for lower λ
values for high SNR (3T) which
is reduced with an increase in λ.
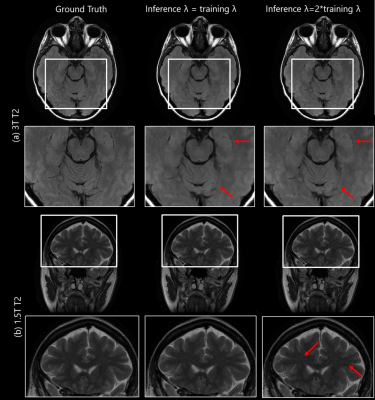
Figure 5: Qualitative comparison of
reconstructions when λ parameter is varied during
inference: The reconstructions for a 3T T2 (higher SNR) and 1.5T T2 (lower SNR)
datasets are shown in top two and bottom two rows respectively. Rows 2 and 4
show the zoomed region corresponding to the white box in rows 1 and 3. We
observed that for 3T datasets, an inference lambda higher than training lambda
yields sharper images (red arrows), whereas for 1.5T datasets it results in
noise amplification.
DOI: https://doi.org/10.58530/2023/4642