4631

Concatenated multi-contrast wavelet-based compressed sensing reconstruction.

Gabriel Varela-Mattatall^1,2, Jaejin Cho^3,4, Omer Oran⁵, Corey A. Baron^1,2, Berkin Bilgic^3,4, and Ravi S. Menon^1,2
¹Centre for Functional and Metabolic Mapping (CFMM), Robarts Research Institute, Western University, London, ON, Canada, ²Department of Medical Biophysics, Schulich School of Medicine and Dentistry, Western University, London, ON, Canada, ³Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital & Harvard Medical School, Boston, MA, United States, ⁴Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Boston, MA, United States, ⁵Siemens Healthcare Limited, Oakville, ON, Canada

Synopsis

Keywords: Image Reconstruction, Image Reconstruction

There is a family of multi-contrast sequences such as MEGRE, MP2RAGE and 3D-QALAS which produce a limited number of contrasts, and their corresponding reconstructions in highly accelerated acquisitions are not optimally represented by either compressed sensing, low rank, or both reconstruction styles together. In this work, we explore a novel way to perform compressed sensing for simultaneous multi-contrast reconstruction. By using a concatenation operator in the regularization term, we can perform a single compressed sensing reconstruction with automatic parameter selection to reconstruct all contrasts at once and provide an implicit form of parallelization for multi-contrast reconstruction.

Introduction

Compressed Sensing (CS)^1,2 sparsely encodes the information of a single contrast image to regularize parallel imaging reconstruction problems. With a larger number of contrasts e.g, tens or hundreds as in fMRI, low rank³ and low rank plus sparse^4,5reconstructions are powerful alternatives to exploit redundancy between contrasts. However, imaging sequences like multi-echo gradient echo (MEGRE), MP2RAGE⁶ and 3D-QALAS⁷ do not produce enough multi-contrast redundancy to optimally benefit from those reconstruction styles. Therefore, an alternative regularization term is required for this imaging regime with a limited number of contrasts.
Different methods have emerged to tackle this problem^8–12. Unfortunately, these methods may not generalize well to different imaging protocols or demand exhaustive parameter tuning. Given these observations, we propose to reconstruct multi-contrast imaging through wavelet-based CS and with automatic selection of the regularization weighting by concatenating contrasts within the regularization term.

Theory

CS reconstruction,
$$\hat{x} = \textrm{argmin}_x \|Ax-y\|_2^2+\lambda\|\Psi x\|_1,\textrm{Eq.(1)}$$
promotes a sparsely encoded reconstruction that complies with both data consistency and regularization constrains. In Eq (1), $$$A$$$ is the encoding forward model with $$$A=SFC$$$, where $$$S$$$ is the sampling pattern, $$$F$$$ is the Fourier Transform, $$$C$$$ are the sensitivity coil maps; $$$y$$$ is k-space, $$$\Psi$$$ stands for the sparsifying transform, and $$$\lambda$$$ is the regularization weighting that balances the two terms in the reconstruction. In our previous work¹³, it was demonstrated that it is possible to determine $$$\lambda$$$ when using the Wavelet transform as the sparsifying transform, $$$W$$$, to obtain a close-to-optimum solution from the wavelet transform of the zero-filled reconstruction ($$$WA^Ty$$$). However, Eq. (1) is limited to a single contrast as it encodes image features through wavelets. Hence, we propose the following modification for the case of a limited number of contrasts,
$$\hat{X}=\textrm{argmin}_X \|AX-Y\|_2^2+\lambda\|\Psi \Omega X\|_1,\textrm{Eq.(2)}$$
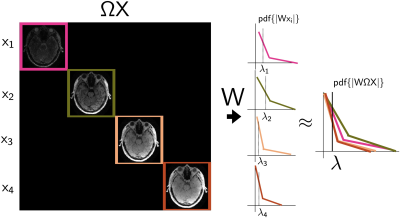
where all contrasts, $$$X$$$, are included. The key difference is a concatenation operator, $$$\Omega$$$, that diagonalizes the contrasts prior to the wavelet transform. Our hypothesis is that the combination of wavelet coefficient distributions from each contrast approximates the overall distribution in this concatenated space, meaning that there exists a single regularization weighting that could be applied to all contrasts at once (Figure 1). The concatenation operation only affects the proximal operator of the regularization term,
$$P_{\lambda \|W\Omega X\|_1}=\Omega^TW^TS_{\lambda}\{W\Omega X\},\textrm{Eq.(2)}$$
where $$$S_{\lambda}$$$ is the soft-thresholding function. Although the diagonalization of contrasts through $$$\Omega$$$ is computationally inefficient, the diagonalization of contrasts and applying the wavelet transform to this concatenated space is equivalent to applying the wavelet transform to each contrast and then stacking up their corresponding wavelet coefficients. Such implementation allows efficient determination of $$$\lambda$$$ as of the iterative reconstruction process.

Methods

MEGRE, MP2RAGE and 3D-QALAS datasets were analyzed in this work. MEGRE and MP2RAGE fully sampled sequences were retrospectively undersampled with either uniform Poisson, Elliptical sampling, or with a small calibration. 3D-QALAS was acquired using uniform acceleration, and further accelerated by intersecting the uniform pattern with a lowly accelerated random pattern. Sequences parameters are as follow:
MEGRE: FOV = 208x208x208 mm; isotropic resolution of 1 mm; TE0/TEΔ/TR = 4.5/4.5/25 ms; 5 echoes; FA = 10;monopolar readout; Bandwidth = 860 Hz/Px; transversal orientation; total acquisition time 18:02.
MP2RAGE: FOV = 256x254x192 mm; isotropic spatial resolution of 1 mm; TE/TI1/TI2/TR = 3.27/900/2500/5000 ms; FA1/FA2 = 4/5; Bandwidth = 200 Hz/Px; total acquisition time: 20:00.
3D-QALAS: FOV = 240x240x176 mm; isotropic spatial resolution of 1.15 mm iso; TE/TR 2.29/4500 ms, TIs 110/1010/1910/2810/3710 ms, FA = 4; Bandwidth = 330 Hz/Px; uniform acceleration factor of 2x1 in PE direction with Elliptical scanning; total acquisition time 8:32.
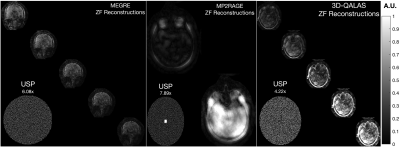
The three datasets underwent the following reconstruction pipeline: a reference scan was used for estimation of sensitivity coil maps using ESPIRIT¹⁴ (Bart toolbox v0.8.00) after coil-compression¹⁵ to 21 virtual coils. Then, an inverse Fourier transform in the readout direction allows parallelization of the reconstruction process and Eq. (2) was implemented with a monotone FISTA algorithm^16,17. Since parallelization is applied along the readout direction, single contrast reconstruction must be applied as a sequential process.The determination of the regularization weighting was based on k-means applied to $$$W\Omega A^TY$$$ and to $$$WA^Ty$$$(which includes modifications on¹³). For the case of $$$W\Omega A^TY$$$, instead of simply stacking up wavelet coefficients, we applied the L2-norm to wavelet coefficients across contrasts to make the determination of more robust to specific contrast-based SNR variations¹⁸. In all experiments reconstruction quality from concatenated CS (cCS) and single contrast CS (sCS) were compared to the reference in terms of NRMSE. Figure 2 shows input data for each case.

Results

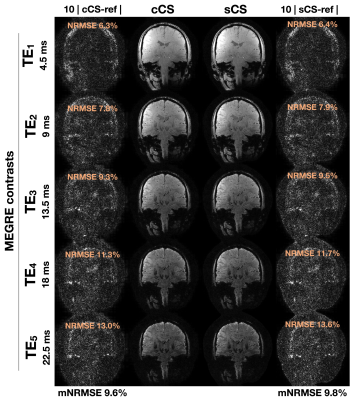
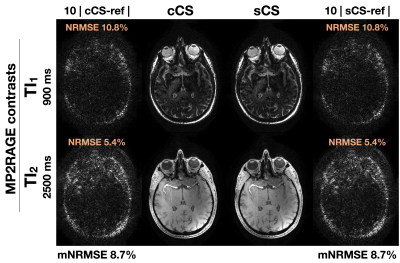
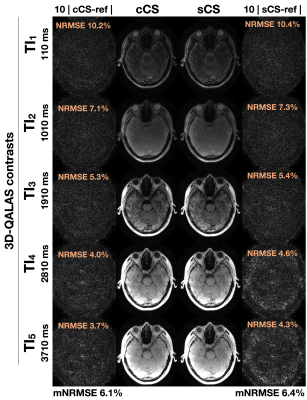
Figures 3-5 show the results from the MEGRE, MP2RAGE and 3D-QALAS datasets, respectively. Differences shown were amplified ten-fold. In both MEGRE and 3D-QALAS reconstructions we quantified a slight improvement under 1% when compared to the reference. In MP2RAGE we did not detect any differences between reconstructions even at 8x undersampling.

Discussion and Conclusion

In this work we have proposed a concatenation operator inside the regularization term of the CS reconstruction model to reconstruct limited multi-contrast imaging, and to estimate the regularization weighting for all contrasts in an automatic manner at once. Furthermore, our proposal provides an implicit form of parallelization that could accelerate the reconstruction process. Results support the flexibility and broad utility of our main finding for faster limited multi-contrast reconstruction.

Acknowledgements

This work was funded by a CIHR Foundation Grant and an NSERC Discovery Grant.This work was funded by NIH grant numbers R01EB028797, R01EB032378, U01EB025162, P41EB030006, U01EB026996, R03EB031175, and NVIDIA gpu.We thank ISMRM for the Exchange research program award.

References

1. Candes EJ, Wakin MB. An Introduction To Compressive Sampling. Ieee Signal Proc Mag. 2008;25(2):21-30. doi:10.1109/msp.2007.914731

2. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnet Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391

3. Cai JF, Candes EJ, Shen Z. A Singular Value Thresholding Algorithm for Matrix Completion. Arxiv. 2008.

4. Otazo R, Candès E, Sodickson DK. Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnet Reson Med. 2015;73(3):1125-1136. doi:10.1002/mrm.25240

5. Cao Z, Gore JC, Grissom WA. Low‐rank plus sparse compressed sensing for accelerated proton resonance frequency shift MR temperature imaging. Magnet Reson Med. 2019;81(6):3555-3566. doi:10.1002/mrm.27666

6. Marques JP, Kober T, Krueger G, Zwaag W van der, Moortele PFV de, Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage. 2010;49(2):1271-1281. doi:10.1016/j.neuroimage.2009.10.002

7. Kvernby S, Warntjes MJB, Haraldsson H, Carlhäll CJ, Engvall J, Ebbers T. Simultaneous three-dimensional myocardial T1 and T2 mapping in one breath hold with 3D-QALAS. J Cardiov Magn Reson. 2014;16(1):102. doi:10.1186/s12968-014-0102-0

8. Bilgic B, Goyal VK, Adalsteinsson E. Multi‐contrast reconstruction with Bayesian compressed sensing. Magnet Reson Med. 2011;66(6):1601-1615. doi:10.1002/mrm.22956

9. Gong E, Huang F, Ying K, Wu W, Wang S, Yuan C. PROMISE: Parallel‐imaging and compressed‐sensing reconstruction of multicontrast imaging using SharablE information. Magnet Reson Med. 2015;73(2):523-535. doi:10.1002/mrm.25142

10. Lai Z, Zhang X, Guo D, et al. Joint sparse reconstruction of multi-contrast MRI images with graph based redundant wavelet transform. Bmc Med Imaging. 2018;18(1):7. doi:10.1186/s12880-018-0251-y

11. Bilgic B, Kim TH, Liao C, et al. Improving parallel imaging by jointly reconstructing multi‐contrast data. Magnet Reson Med. 2018;80(2):619-632. doi:10.1002/mrm.27076

12. Bustin A, Cruz GL da, Jaubert O, Lopez K, Botnar RM, Prieto C. High‐dimensionality undersampled patch‐based reconstruction (HD‐PROST) for accelerated multi‐contrast MRI. Magnet Reson Med. 2019;81(6):3705-3719. doi:10.1002/mrm.27694

13. Varela‐Mattatall G, Baron CA, Menon RS. Automatic determination of the regularization weighting for wavelet‐based compressed sensing MRI reconstructions. Magnet Reson Med. 2021;86(3):1403-1419. doi:10.1002/mrm.28812

14. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magnet Reson Med. 2014;71(3):990-1001. doi:10.1002/mrm.24751

15. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magnet Reson Med. 2007;57(6):1131-1139. doi:10.1002/mrm.21237

16. Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. Siam J Imaging Sci. 2009;2(1):183-202. doi:10.1137/080716542

17. Zibetti MVW, Helou ES, Regatte RR, Herman GT. Monotone FISTA With Variable Acceleration for Compressed Sensing Magnetic Resonance Imaging. Ieee Transactions Comput Imaging. 2018;5(1):109-119. doi:10.1109/tci.2018.2882681

18. Murphy M, Alley M, Demmel J, Keutzer K, Vasanawala S, Lustig M. Fast $\ell_1$-SPIRiT Compressed Sensing Parallel Imaging MRI: Scalable Parallel Implementation and Clinically Feasible Runtime. Ieee T Med Imaging. 2012;31(6):1250-1262. doi:10.1109/tmi.2012.2188039

Figures

Figure 1- Conventionally, the regularization weighting, $$$\lambda_i$$$ , needs to be determined for each contrast by analyzing the distribution of wavelet coefficients from the zero-filled reconstruction, and then apply compressed sensing reconstruction. In here, we propose to diagonalize contrasts, and apply the wavelet transform to the concatenated space, $$$\Omega X$$$, to determine a that allows multi-contrast reconstruction in a single reconstruction problem.

Figure 2- Zero-filled reconstructions from MEGRE, MP2RAGE and 3D-QALAS contrasts. Images include the undersampling pattern and acceleration factor used for reconstructions.

Figure 3- Comparison between the proposed concatenated compressed sensing (cCS) and standard single contrast compressed sensing (sCS) reconstructions for MEGRE contrasts. The reference had k-space samples out of the imposed elliptical pattern, which explains the slight difference around borders.

Figure 4- Comparison between the proposed concatenated compressed sensing (cCS) and standard single contrast compressed sensing (sCS) reconstructions for MP2RAGE contrasts. The reference had k-space samples out of the imposed elliptical pattern, which explains the slight difference around borders.

Figure 5- Comparison between the proposed concatenated compressed sensing (CS) and standard single contrast compressed sensing (sCS) for 3D-QALAS contrasts.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

4631

DOI: https://doi.org/10.58530/2023/4631