4630
K-space Based Motion Estimation for polar fMRI using Transfer learning
Faeze makhsousi1, Vahid Ghodrati2, Morteza Homayounfar1, sina ghaffarzadeh1, and abbas Nasiraei-Moghaddam3
1Biomedical Engineering, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran (Islamic Republic of), 2University of California, Los Angeles, Los Angeles, CA, United States, 3Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran (Islamic Republic of)
1Biomedical Engineering, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran (Islamic Republic of), 2University of California, Los Angeles, Los Angeles, CA, United States, 3Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran (Islamic Republic of)
Synopsis
Keywords: Motion Correction, Brain, Data Analysis
The motion of the head during functional MRI is an unavoidable issue that adversely affects brain mapping. Radial reading of the k-space reduces the problem to some extent but not completely. Residual motion, even at a partial pixel level, has a measurable effect on the spatial frequencies and so can be estimated directly from the k-space data. This work uses a transfer learning-based approach to estimate the head motion from radially acquired k-space information. Results showed a good agreement with the statistical parametric mapping (SPM) package.Introduction
Estimation and correction of the head rigid-body motion are necessary steps prior to the analysis of the functional Magnetic Resonance Imaging (fMRI), which usually takes place in the imaging domain. These steps are particularly important for high-resolution, high-specificity fMRI studies. This type of motion comprises of rotation and simple translation. Where the former results in an identical rotation in k-space, the latter induces a linear phase shift in the spatial frequency domain. Therefore, the k-space phase should be enough for extracting the head's gross motion in consecutive frames on MR images. It suggests that k-space data can be used for the estimation of the residual motion. This would be of special interest in the radial acquisition, which is known for its motion robustness through the oversampling of the k-space center.In this work, we presented a method benefiting from transfer learning to extract residual motion parameters directly from the acquired raw k-space data. This can be a perfect match to the polar fMRI that has been recently developed for high-resolution high-specificity fMRI [1].
Methods
A balanced steady-state free precession sequence, with the radial reading of k-space, was acquired from 28 normal volunteers on a 3T MRI scanner (Siemens, Trio Tim). All volunteers provided a written informed consent. Four successive 2D planes of the head were frequently imaged by a 12-channel head coil during a block-design task-based fMRI study as described in [1]. For each of the 28 normal participants, 70 measurements were performed using the following parameters: TR/TE = 6.12/3.06 ms, FOV = 224x224 mm2, number of Phase-Enc./Spokes = 112, Flip Angle = 30°, Pixel size = 2×2 mm2, slice thickness = 3 mm. K-space raw data was collected for all channels in addition to images that were reconstructed by the scanner through the re-gridding process. The SPM package was used to extract the ground truth motion parameters from each set of images considering the first listed image as the reference for that set. We randomly divided the acquired data into two sets: 1) a train set (25 subjects) and 2) a test set (3 subjects). Considering the fact that the subtraction of two frames could minimize the effect of the stationary objects, we subtracted all successive radial k-spaces from the first one[2] and then fed their phases to the proposed network to directly estimate the 3 translations and 3 rotation angles from radial k-space data.As shown in Fig.1, the proposed neural network contains the pre-trained EfficientNet [3] as the backbone followed by three dense layers with 1024, 1024, and 512 neurons. The LeakyRelu activation function and dropout between layers were also included in the network structure.
We used a single neuron with a Sigmoid activation function for the last layer of our motion estimation model. It is important to note that we trained 6 separate networks to estimate the motion parameters. We used the step-decay learning scheme with an initial learning rate of 10-3 which drops by 10 every 15 epochs. In total, we trained the network for 60 epochs. The model is implemented using the Tensorflow framework and is trained with Adam optimizer and Mean Square Error as a loss function and a batch size of 16 for 60 epochs on the NVIDIA Tesla P100 GPU.
To evaluate the network's performance, we reported R-square and the correlation between the actual induced motion and the one estimated by the network as well as the RMSE between the actual motion parameters and the estimated parameters by the proposed network.
Results
All datasets ( 1960 volumes) were analyzed by SPM and showed that the actual motion did not exceed 1.85 mm and 2.05° for translation and rotation, respectively. Fig. 2 depicts the network predictions for rotation angle and translation motion for the test datasets in comparison to those resulted from SPM. Correlations between our estimated results and those by SPM are greater than 83 percent for all parameters over all test volumes. The correlations as well as RMSE between two methods for all 6 motion parameters are summarized in Table 1. It shows that the in-plane motion is limited to 32 microns and in general, the model output nicely follows the pattern detected by SPM.Discussion
High-resolution/high-specificity fMRI studies are very sensitive to motion, since even the minor residual motions may result in significant errors in detecting active voxels. This study develops an effective supervised technique relying on a deep neural network and transfer learning to estimate fMRI motion directly from k-space. In contrast to the SPM package which is purely based on the image space, the proposed method used the rich information embedded in the k-space data to estimate the motion parameters. Although the technique was applied for motion correction in ssfp-based fMRI studies [1], it is not limited to this type of sequence.As a future direction, we will try to learn all six motion parameters in a single network. In addition, we will use more training and testing data to improve the performance of the network and to achieve a much more solid evaluation.
Acknowledgements
No acknowledgement found.References
1. Malekian V, Rastegar F, Shafieizargar B, Nasiraei-Moghaddam A. SSFP fMRI at 3 tesla: Efficiency of polar acquisition-reconstruction technique. Magnetic Resonance Imaging. 2020 Dec;74:171-180. DOI: 10.1016/j.mri.2020.09.005. PMID: 32898650.
2. Caparelli EC, Tomasi D, Arnold S, Chang L, Ernst T. k-Space based summary motion detection for functional magnetic resonance imaging. Neuroimage. 2003 Oct;20(2):1411-8. doi: 10.1016/S1053-8119(03)00339-2. PMID: 14568510.
3. Tan, M., & Le, Q. (2021, July). Efficientnetv2: Smaller models and faster training. In International Conference on Machine Learning (pp. 10096-10106). PMLR.
Figures
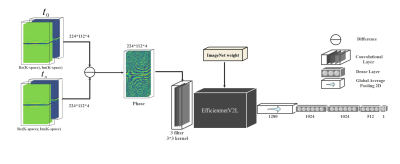
Fig 1. The proposed model
is trained to estimate motion parameters from the phase of radial k-space. The
input to the network is the
difference between the first volume of k-space acquired at time t0
as a reference volume and successive time points.
The last layers are modified to the regression layers that predict the motion
parameters
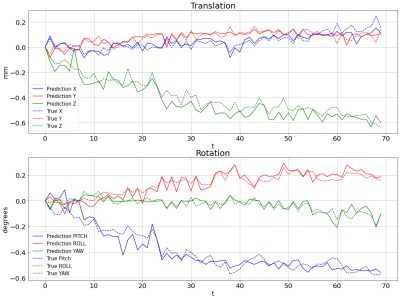
Fig 2: The average of the prediction of translation and
rotation motions over the test cases compared to the average of the motion
parameters extracted from SPM; (a), the prediction of three translations along
(x, y, z) axes; (b), the prediction of the three rotations around (x, y, z)
axes.
Table 1. The average values of R-square,
correlation and RMSE between estimated motion parameters with motion parameters
extracted from SPM for the test cases. RMSE for translation and rotation are in
mm and degree, respectively.
DOI: https://doi.org/10.58530/2023/4630