4626
Accelerated Calibrationless MR Parametric Mapping by a Space-Contrast-Coil-Domain Locally Low-Rank Tensor Constraint1Institute of Medical Imaging Technology, School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Department of Cardiovascular Medicine, Ruijin Hospital Lu Wan Branch, Shanghai Jiao Tong University School of Medicine, Shanghai, China
Synopsis
Keywords: Sparse & Low-Rank Models, Quantitative Imaging
Parametric mapping is routinely used in cardiac MR, yet its resolution is relatively low due to the single-shot acquisition. Most existing acceleration methods exploit the space-contrast-domain and coil-domain information redundancy separately e.g. by combining LLR and SENSE. Here we propose a novel calibrationless parametric mapping acceleration technique based on a Locally Low-Rank Tensor (LLRT) modeling of the signal in the space-contrast-coil domain, which exploits the information redundancy over all 3 dimensions jointly. In vivo studies show that the method generates more accurate reconstructions than the LLR-based algorithm. Moreover, a nonuniform LLRT penalty further improves the reconstruction quality by reducing blurring.Introduction
Parametric mapping1,2 represents a set of important tissue characterization techniques for cardiac MR. However, the resolution of cardiac parametric mapping is relatively low due to the single-shot acquisition. Existing acceleration methods include compressed sensing3 , Locally Low Rank (LLR)4, and parallel imaging5, which exploit information redundancy along the space, space-contrast, and coil domain, respectively. However, the space-contrast-domain redundancy and coil-domain redundancy are typically separately modeled, e.g. by combining LLR with SENSE6 or SPIRiT4. To our knowledge, whether a further redundancy exists in the space-coil domain and contrast-coil domain has not been investigated. Here we propose a novel calibrationless parametric mapping acceleration algorithm based on a joint Locally Low-Rank Tensor (LLRT) modeling of the signal in the space-contrast-coil domain. We show that the algorithm achieves more accurate reconstruction in 2D radial undersampled cardiac T1 mapping.Methods
Figure 1 shows the concept of the proposed method. The LLRT property of the multi-coil multi-contrast images is exploited by performing a 3-way Tucker decomposition of the signal in each spatial block of the image domain. The sparsity of the core tensor is enforced by minimizing the $$$l_1$$$ norm of the vectorized core tensor. The cost function is formulated as: $$\min _{\boldsymbol{x}} \frac{1}{2}\|\boldsymbol{y}-\boldsymbol{D} \boldsymbol{F} \boldsymbol{x}\|_{\mathrm{F}}^{2}+\alpha\|\boldsymbol{x}\|_{\text {LLRT }}$$where $$$y$$$ the measured k-space data, $$$D$$$ the density compensation matrix; $$$F$$$ the Fourier transform evaluated at the sampled k-space locations; $$$x$$$ the unknown image in the space-contrast-coil domain, $$$\alpha$$$ the weight of the LLRT regularization, and $$$\|\cdot\|_{\text {LLRT }}$$$ the LLRT constraint. We developed a reconstruction algorithm based on the Alternating Direction Method of Multipliers to solve the problem in Eq 1. Notice that since coil sensitivity maps are not needed in the reconstruction, the proposed method is calibrationless, which is potentially useful to reduce errors caused by inaccurate calibration.We developed two LLRT constraints, which respectively apply a uniform and a nonuniform penalty to the core tensor values. The use of nonuniform penalty is based on the observation that the core values do not monotonically decrease as the singular values do in singular value decomposition. For example, the core values corresponding to a heading principal component along certain dimension can be smaller than those corresponding to a set of tailing principal components. A uniform penalty may cause false removal of important principal components from the tensor, resulting in blurring or inaccurate reconstruction. To address the issue, the nonuniform LLRT penalty linearly varies its weight along the three dimensions based on indexes of the core value in the core tensor. The algorithms based on the uniform and nonuniform LLRT constraints are called “uLLRT” and “nLLRT”, respectively.
MOLLI cardiac T1 mapping with no undersampling or interleaved radial undersampling was performed in four healthy subjects (2 Male, age 23±1) with standard spine and torso coils in a 3T scanner (uMR790, United Imaging) after obtaining written informed consent. For the dataset without undersampling, radial-undersampled data were retrospectively generated by performing nonuniform FFT to the raw images. The proposed uLLRT and nLLRT reconstructions were compared with a previously developed LLR-SENSE algorithm6 with maximally 8-fold accelerations. Typical sequence parameters were: minimum TI=110-145ms, TI increment = 80ms, FOV=320mm×320mm, slice thickness=8mm, bandwidth=1400 Hz/pixel, TR=3.3ms, flip angle=70°.
Results
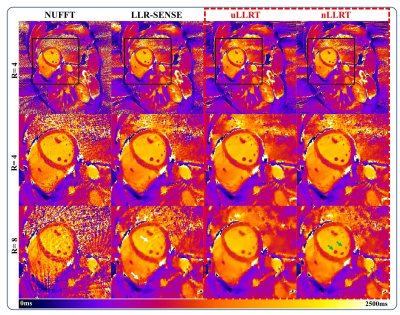
Figure 2 shows reconstruction results for the retrospectively undersampled cardiac T1 mapping in one subject. uLLRT showed reduced NRMSE compared with LLR-SENSE for all 3 acceleration rates. nLLRT showed a further reduction of NRMSE at R=8 compared with uLLRT, and less blurring which is evident from reconstruction of the papillary muscle (green arrows).Figure 3 shows the T1-map reconstruction of prospectively undersampled data at R=4 and 8 in one subject. At R=4, LLR-SENSE and the two LLRT algorithms all led to high-quality reconstructions, with LLRT reconstruction appearing less noisy. At R=8, both LLRT reconstructions were better than the LLR-SENSE reconstruction, which showed stronger aliasing artifacts highlighted by the white arrows. Furthermore, the nLLRT reconstruction was less blurred compared with the uLLRT reconstruction. The myocardium-blood boundary in the nLLRT reconstruction appeared sharper (green arrows).
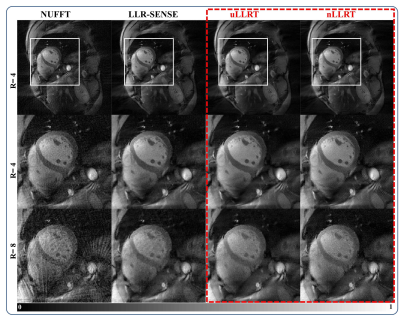
Figure 4 shows the first image with the minimal TI reconstructed from each method from the same subject shown in Figure 3. At R=8, both LLRT reconstructions led to reduced aliasing artifacts compared with LLR-SENSE. The raw images looked similar between uLLRT and nLLRT, with the latter still appearing slightly sharper.
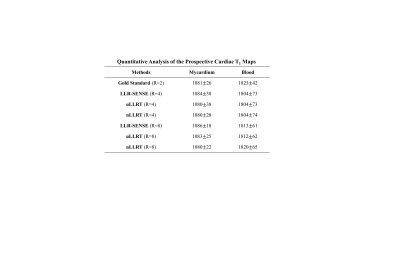
Table 1 shows the quantitative comparison of the average myocardial and blood T1 values between the gold standard (R=2 from parallel imaging) and the three methods (R=4 or 8). Notice that prospectively undersampled reconstruction had a higher resolution than the gold standard (1.25mm×1.25mm vs 1.67mm×1.67mm). Both myocardial and blood T1s are similar between the gold standard, LLR-SENSE, and the two LLRT reconstructions.
Discussion and Conclusions
In this work, we propose a novel acceleration method for parametric mapping using a space-contrast-coil-domain locally low-rank tensor constraint. The method does not need prior reconstruction of coil sensitivity maps or kernels, and exploit the information redundancy between all 3 dimensions for acceleration. The results show that the method achieves a better reconstruction compared with LLR-SENSE for radial undersampled cardiac T1 mapping. A nonuniform penalty on the LLRT core tensor can further improve the reconstruction quality by reducing blurring.Acknowledgements
No acknowledgement found.References
1. Han, P., et al. Electrocardiogram-less, free-breathing myocardial extracellular volume fraction mapping in small animals at high heart rates using motion-resolved cardiovascular magnetic reesonance multitasking: a feasibility study in a heart failure with preserved ejection fraction rat model. J Cardiovasc Magn R 23(2021).
2. Wang, X.Q., et al. Model-based myocardial T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH cardiovascular magnetic resonance. J Cardiovasc Magn R 21(2019).
3. Lustig, M., Donoho, D. & Pauly, J.M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 58, 1182-1195 (2007).
4. Zhang, T., Pauly, J.M. & Levesque, I.R. Accelerating Parameter Mapping with a Locally Low Rank Constraint. Magn Reson Med 73, 655-661 (2015).
5. Lustig, M. & Pauly, J.M. SPIRiT: Iterative Self-consistent Parallel Imaging Reconstruction From Arbitrary k-Space. Magn Reson Med 64, 457-471 (2010).
6. da Cruz, G.L., et al. Sparsity and locally low rank regularization for MR fingerprinting. Magn Reson Med 81, 3530-3543 (2019).
Figures
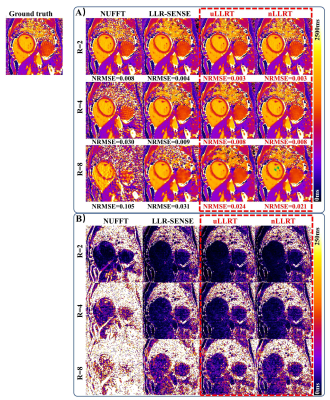
Figure 2. Results of the retrospective cardiac T1 mapping experiment. NRMSE is shown below each image. Panel A shows the T1 maps reconstructed by NUFFT, LLR-SENSE, uLLRT and nLLRT at 2, 4 and 8-fold accelerations. Panel B shows the difference between the reconstructed T1 maps and gold standard. Notice that both LLRT algorithms led to reduced NRMSE compared with LLR-SENSE. At R=8, nLLRT further improved the NRMSE and reduced blurring compared with uLLRT.