4625
New Theory and Faster Computations for Subspace-Based Sensitivity Map Estimation1University of Southern California, Los Angeles, CA, United States
Synopsis
Keywords: Parallel Imaging, Sparse & Low-Rank Models
Sensitivity map estimation is important in many multichannel MRI applications. Subspace-based sensitivity map estimation methods like ESPIRiT are popular and perform well, though can be computationally expensive and their theoretical principles can be nontrivial to understand. In this work, we derive a new theoretical framework for sensitivity map estimation from a structured low-rank modeling perspective. This results in an estimation approach that is equivalent to ESPIRiT, but with theory that may be more intuitive for some readers. In addition, we propose a set of computational acceleration techniques that enable substantial (~25-fold) improvements in computational time for subspace-based sensitivity map estimation.Introduction
Sensitivity maps can be useful for modeling multichannel MRI data1, and a variety of powerful sensitivity map estimation methods have been proposed over the years2-8. Among these, subspace-based estimation methods like ESPIRiT8 have become widely used because of their ease-of-use and excellent performance. However, the theoretical principles underlying subspace-based methods can be nontrivial to understand, and existing subspace-based algorithms can be computationally expensive (which can be especially burdensome when working with large datasets, as in modern machine learning). In this work, we provide new insights into subspace-based sensitivity map estimation by deriving a new nullspace-based method that is mathematically equivalent to ESPIRiT, but which is explained from a different (complementary) perspective that may be more intuitive for some readers. Specifically, our derivations are based on concepts from the structured low-rank modeling literature9,10. In addition to these novel theoretical contributions, we also propose a variety of different computational acceleration techniques. These techniques -- which we collectively call PISCO (Power iteration over simultaneous patches, Interpolation, ellipSoidal kernels, and FFT-based COnvolution) -- can be used with arbitrary subspace-based sensitivity map estimation methods (including both ESPIRiT and our new approach), and enable substantial speed improvements.Theory
Nullspace-Based MethodLet $$$s_\ell(n{\Delta}k)$$$ denote Nyquist-sampled k-space data for the $$$\ell$$$th channel, with a total of $$$L$$$ channels. The image reconstruction literature on structured low-rank modeling9,11-13 has established that it is possible to find a large number of multichannel finite-impulse response (FIR) filters such that $$\sum_{\ell}s_\ell(n{\Delta}k){\circledast}h^{(r)}_\ell(n{\Delta}k){\approx}0,$$ where $$$\circledast$$$ denotes convolution and $$$h^{(r)}_\ell(n{\Delta}k)$$$ is the $$$\ell$$$th channel of the $$$r$$$th FIR filter. This can be expressed in the image domain as $$\rho(x)\sum_{\ell}c_\ell(x)h_\ell^{(r)}(x){\approx}0,$$ where $$$\rho(x)$$$ is the underlying image, $$$c_\ell(x)$$$ is the sensitivity map for the $$$\ell$$$th channel, and $$$h_\ell^{(r)}(x)$$$ is the inverse transform of $$$h^{(r)}_\ell(n{\Delta}k)$$$. This expression implies that if we form an $$$R{\times}L$$$ matrix $$$\mathbf{H}(x)$$$ with $$$(r,\ell)$$$th entry equal to $$$h_\ell^{(r)}(x)$$$, then the $$$L{\times}1$$$ vector of sensitivity profiles $$$c_\ell(x)$$$ will be a nullspace vector of $$$\mathbf{H}(x)$$$ at spatial locations where $$$\rho(x){\neq}0$$$. Empirically, it is observed that $$$\mathbf{H}(x)$$$ only has a single nullspace vector within the image support. This allows sensitivity maps to be estimated by: (1) using calibration data to find the filters $$$h^{(r)}_\ell(n{\Delta}k)$$$,14 (2) calculating $$$\mathbf{H}(x)$$$, and (3) obtaining sensitivity maps from the nullspaces of $$$\mathbf{H}(x)$$$.
This approach can be shown to be mathematically equivalent to ESPIRiT8, although the derivations of the two approaches are very distinct and complementary.
PISCO
The PISCO approach is based on combining multiple acceleration techniques together. First, we observe that we can estimate the filters $$$h^{(r)}_\ell(n{\Delta}k)$$$ using efficient convolutional techniques, like similar approaches developed for structured low-rank image reconstruction15-17. We also use the fact that using ellipsoidal filter kernels offers substantial memory advantages over standard rectangular kernels18. We also observe that the smoothness of sensitivity maps allows us to save computation by estimating them at low resolution and then interpolating to higher resolution. Finally, we find the nullspace of $$$\mathbf{H}(x)$$$ for all voxels simultaneously by using the simple/efficient Power Iteration method19.
Methods
ESPIRiT and the nullspace-based approach were implemented in MATLAB. Performance was assessed using a 32-channel T2-weighted dataset as shown in Fig. 1. We estimated sensitivity maps using different amounts of calibration data. The accuracy of estimated sensitivity maps was evaluated by projecting high-resolution images onto the subspace spanned by the sensitivity maps8. Computation times were measured on a computer with an Intel Xeon E5-1603 2.8GHz quad core CPU.Results
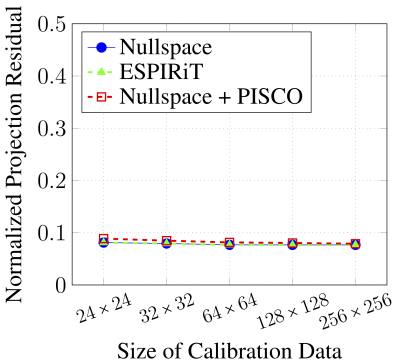
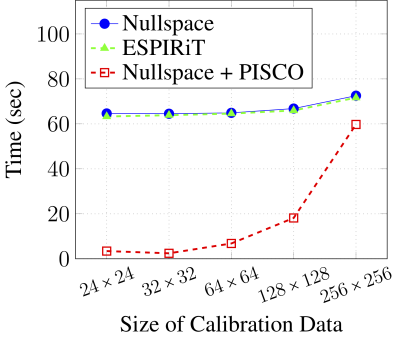
Figure 2 shows the eigenvalues of the matrices $$$\mathbf{H}(x)$$$. As expected, there is a unique nullspace vector at spatial locations where $$$\rho(x){\neq}0$$$. (The matrix does not have a nullspace when $$$\rho(x)=0$$$). Figure 3 shows that the accuracy of the nullspace-based approach is equivalent to that of ESPIRiT, and that combining the nullspace-based approach with PISCO does not compromise accuracy. Figure 4 shows representative sensitivity maps that were estimated from 24$$$\times$$$24 calibration data, demonstrating negligible visual differences. Figure 5 demonstrates that PISCO offers substantial computational accelerations over conventional implementations, enabling up to 25-fold acceleration. To make the comparisons as fair as possible, the times reported in Fig. 5 are all based on in-house MATLAB implementations. It is worth noting that the BART20 software package provides an efficient C-based implementation of ESPIRiT. While C-based implementations are generally expected to be much faster than MATLAB implementations, our PISCO-based MATLAB implementation is actually much faster than the C-based BART implementation. For example, with 24$$$\times$$$24 calibration data, our PISCO-based MATLAB implementation completed in 3.4 seconds, while the C-based BART implementation was slower at 18.9 seconds. It is expected that a C-based implementation of PISCO would be even faster.Discussion and Conclusions
We derived a new theoretical framework for subspace-based sensitivity map estimation based on principles from structured low-rank modeling. This leads to a nullspace-based sensitivity map estimation method that is mathematically equivalent to ESPIRiT, but which has a distinct justification that will potentially be more intuitive to some readers. In addition, we introduced the set of PISCO computational accelerations for subspace-based sensitivity map estimation that enable substantial reductions in computation time. While we only illustrated the combination of PISCO with the nullspace-based approach, the same principles can also be applied to other subspace-based estimation methods.Acknowledgements
This work was supported in part by NIH grants R01-MH116173 and NIH R01-NS074980 and the Ming Hsieh Institute for Research on Engineering-Medicine for Cancer.References
[1] Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. “The NMR phased array”. Magnetic Resonance in Medicine 16:192-225, 1990.
[2] Sodickson DK, Manning WJ. “Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays”. Magnetic Resonance in Medicine 38:591-603, 1997.
[3] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. “SENSE: sensitivity encoding for fast MRI”. Magnetic Resonance in Medicine 42:952-62, 1999.
[4] Walsh DO, Gmitro AF, Marcellin MW. “Adaptive reconstruction of phased array MR imagery”. Magnetic Resonance in Medicine 43:682-90, 2000.
[5] Bydder M, Larkman DJ, Hajnal JV. “Combination of signals from array coils using image‐based estimation of coil sensitivity profiles”. Magnetic Resonance in Medicine 47:539-48, 2002.
[6] Ying L, Sheng J. “Joint image reconstruction and sensitivity estimation in SENSE (JSENSE)”. Magnetic Resonance in Medicine 57:1196-202, 2007.
[7] Uecker M, Hohage T, Block KT, Frahm J. “Image reconstruction by regularized nonlinear inversion—joint estimation of coil sensitivities and image content”. Magnetic Resonance in Medicine 60:674-82, 2008.
[8] Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. “ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA”. Magnetic Resonance in Medicine 71:990-1001, 2014.
[9] Haldar JP, Setsompop K. "Linear Predictability in MRI Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging”. IEEE Signal Processing Magazine 37:69-82 2020.
[10] Jacob M, Mani MP, Ye JC. “Structured low-rank algorithms: Theory, magnetic resonance applications, and links to machine learning”. IEEE Signal Processing Magazine 37:54-68, 2020.
[11] Haldar JP. "Low-rank modeling of local-space neighborhoods (LORAKS) for constrained MRI”. IEEE Transactions on Medical Imaging 33:668-681, 2014.
[12] Haldar JP, Zhuo J. "P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data”. Magnetic Resonance in Medicine 75:1499-1514, 2015.
[13] Jin KH, Lee D, Ye JC. “A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix”. IEEE Transactions on Computational Imaging 2:480-95, 2016.
[14] Haldar JP. “Autocalibrated LORAKS for fast constrained MRI reconstruction”. Proc. IEEE International Symposium on Biomedical Imaging 2015, pp. 910-913.
[15] Ongie G, Jacob M. “A fast algorithm for convolutional structured low-rank matrix recovery”. IEEE Transactions on Computational Imaging 3:535-50, 2017.
[16] Kim TH, Bilgic B, Polak D, Setsompop K, Haldar JP. “Wave‐LORAKS: Combining wave encoding with structured low‐rank matrix modeling for more highly accelerated 3D imaging”. Magnetic Resonance in Medicine 81:1620-33, 2019.
[17] Zhao S, Potter LC, Ahmad R. “High‐dimensional fast convolutional framework (HICU) for calibrationless MRI”. Magnetic Resonance in Medicine 86:1212-25, 2021.
[18] Lobos RA, Haldar JP. “On the shape of convolution kernels in MRI reconstruction: Rectangles versus ellipsoids”. Magnetic Resonance in Medicine 87:2989-96, 2022.
[19] Golub GH, Van Loan CF. Matrix Computations, 3rd ed. London: The Johns Hopkins University Press, 1996.
[20] Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. “Berkeley advanced reconstruction toolbox”. Proc. Intl. Soc. Mag. Reson. Med. 2486, 2015.
Figures