Synopsis

Keywords: Pulse Sequence Design, Sparse & Low-Rank Models

T₂ mapping is an important biomarker for pre-clinical imaging to characterize the grows of metastasis but suffers from long acquisition time when performed in 3D. Undersampling of the k-space combined to advanced iterative reconstruction using the temporal redondancy of the data along the echo train could be beneficial to reach a reasonable scan time. This works demonstrates that a subspace-based reconstruction for T₂ mapping can be used to accelerate a 3D Multi-Echo Spin-Echo acquisition for in-vivo mouse brain metastasis quantification with an acceleration factor up to 10 while keeping an isotropic spatial resolution of 156µm.

Introduction

T₂ mapping is of great interest in neuro-imaging for multiple pathologies and in oncology, as T₂-mapping can be a biomarker for treatment response assessment and brain metastasis characterization [1]. In preclinical setting, T₂ mapping is usually retrieved from a Multi-Echo Spin-Echo acquisition (MESE). This sequence suffers from long acquisition time and is mostly performed with a 2D Multi-Slice protocol which limits the spatial resolution hence the ability to detect and characterize small metastasis. In this works, we developed an undersampled MESE sequence with a different mask for each echo and evaluated the impact of a subspace-based reconstruction [2,3] on the T₂ mapping accuracy and image quality when applied on a mouse model of brain metastasis.

Methods

Materials
Experiments were performed on a 7 T Bruker BioSpec system and a 4‐element (2 ×2)‐phased array surface reception coil. Acquisition were performed on MnCl₂ tubes (T2=10/30/111/152/366 ms) and on mice (N=3) with brain metastasis.

Sequence and protocols
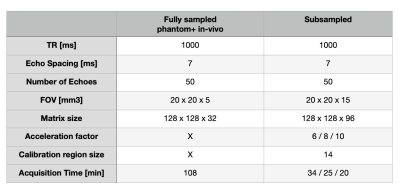
A custom MESE sequence was implemented in order to accelerate the acquisition. The cartesian encoding trajectory was modified to obtain (1) a variable density Poisson sampling mask along the ky‐kz plane, (2) which is variable across echoes and (3) to fully sampled the central part of k-space. The main parameters of the sequence are summarised in table 1.

Reconstruction
The k-spaces were extracted with MRIReco.jl toolbox [4] and the reconstruction steps were performed with the BART toolbox [5]. Images were reconstructed with a subspace-constrained approach [2,3] by minimizing the following equation :
$$\min_x \frac{1}{2}||y - E \Phi_K \alpha||^2_2 + \lambda||W(\alpha)||_1$$
where y is the k-space data, E is the encoding operator regrouping the FFT operator and the coil sensitvity operator, $$$\Phi_K$$$ is the orthonormal temporal basis cropped to the first K basis, $$$\alpha$$$ is the temporal basis coefficient and W corresponds to the Wavelet Operator. The temporal basis were composed of exponential curves with T₂ ranging linearly from 1 to 2000 ms with a 1 ms steps. The first echo was used to generate the coil sensitivity maps. Fully acquisitions were reconstructed with the same processing without the use of basis and with only 1 iteration.

T₂ maps were generated from the reconstructed images using a custom package (https://github.com/aTrotier/qMRI.jl) which fits the following equation that takes into account the noise level [6] :
$$S(t) = \sqrt{(M_0 \exp(-\frac{t}{T_2}))^2 + \sigma_g^2}$$

Results

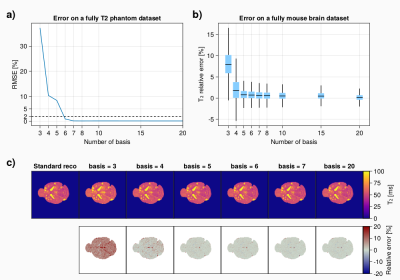
T₂ mapping accuracy
The number of basis required to obtain an accurate measurement of T₂ has been investigated by reconstructing fully-sampled acquisition on a phantom and mouse brain with metastasis.On phantom, the root median square error (RMSE) between the T₂ maps (Fig 1.a) reconstructed with and without the subspace pipeline suggest that a number of basis=6 is required to obtained a RMSE<5% over the large range of T₂ measured. Performing the same analysis in-vivo from a mouse brain with metastasis (Fig 1.b) shows that a number of basis=5 is enough to get almost all of the voxel error under 5% (Fig 1.c), the relative error maps are equivalent between basis=5 and basis=20. Basis=3 exhibits an offset error but it should be pointed out that basis=4 only shows differences in some pixels

Retrospective undersampling
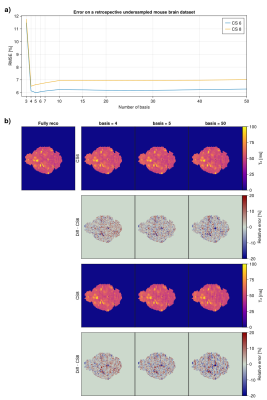
When performing a subspace-based reconstruction on undersampled acquisitions, the number of basis also impacts the quality of the reconstruction, hence the error on the T₂ maps. To assess that effect, a retrospective undersampled mouse brain dataset has been reconstructed with a number of basis from 3 to 50 and compared against the fully-sampled acquisition. For an acceleration factor of 6 or 8, the RMSE (Fig 2.a) shows a minimum value at a number of basis=4 or 5 respectively. For CS6, undersampling artefacts in the form of stripes are more pronounced with basis=50 than basis=4/5 (Fig 2.b).

Prospective undersampling
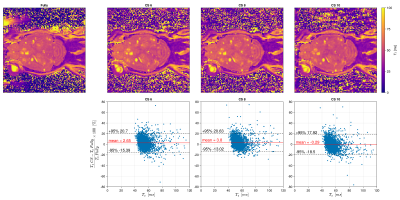
Prospective acquisitions with an acceleration factor of CS=6/8/10 have been reconstructed and compared to a fully sampled acquisition (Fig 3). Even with CS=10, the cerebellum structure can be easily depicted. Small metastasie of the order of few voxels are well identified on all CS accelerations. Bland-altman plots show an error<5%. Standard deviation for CS=6/8/10 is stable along the acceleration factor (respectively 9.2/8.6/9.3%)

Discussion

A number of basis equal to 5 gives the better compromise in-vitro and in-vivo between T₂ accuracy, acquisition time, smoothness of the maps and seems robust to prospective undersampling for the 3 acceleration factors investigated. Interestingly retrospective undersampling performed on one slice results in lower image quality in the form of stripes artefacts than the one acquired prospectively, this might be due to the difference in the acquisition protocols. On prospective acquisitions, the standard deviation is constant (approximatively 10%) for all acceleration factors, the increase of error expected might be hiden by the interscan motion between the fully-sampled and accelerated acquisitions.

Conclusion

Subspace-based reconstruction is suitable for 3D T2 mapping. Our analysis suggests that a number of basis equal to 5 is enough to get a good accuracy. This methods can be used to reach an acceleration factor up to 10 corresponding to a duration of 20 minutes for a 3D acquisition with 156µm on mouse brain with small metastasis.

Acknowledgements

This work was supported by the French National Research Agency (ANR-19-CE19-0014) and by the Inserm Cancer PCSI funding N°20CP093-00.