4623
In Vivo xSPEN Imaging with a Model-Based Reconstruction for Efficient Spatial Encoding in a Single-Sided Prostate MRI Scanner
Muller De Matos Gomes1, Meredith Sadinski1, Alek Nacev1, and William Allyn Grissom2
1Promaxo, Oakland, CA, United States, 2Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
1Promaxo, Oakland, CA, United States, 2Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
Keywords: New Trajectories & Spatial Encoding Methods, Image Reconstruction, Low-Field MRI, Spatiotemporal Encoding
Single-sided low-field MRI scanners can provide image guidance during interventions such as prostate biopsies without restricting surgical access, but efficient spatial encoding is a challenge. In this work we show how spatiotemporal encoding using the xSPEN method combined with a model-based image reconstruction enables swapping a conventionally phase encoded but large-matrix-size image dimension with a conventionally frequency encoded but small-matrix-size image dimension. The model-based reconstruction yields images free of distortions due to gradient non-linearity and shows overall improved in vivo male pelvic image quality.Introduction
Single-sided low-field MRI scanners can provide image guidance during interventions such as prostate biopsies without restricting surgical access. The Promaxo scanner in Figure 1 (Promaxo, Oakland, CA, USA) is such a system and has a built-in 58-73 mT z-gradient. Imaging on this scanner is performed using a multi-slab 3D sequence in which the large matrix dimensions (100s of voxels; x and y) are phase-encoded by the pulsed x and y gradients, while the small matrix dimension (10s of voxels; z) is frequency encoded by the fixed z gradient. This leads to clinically acceptable anatomic scan times less than 10 minutes. However, faster scans are desirable for localizers and intraoperative imaging but are fundamentally limited by the fact that the fastest spatial encoding mechanism (frequency encoding) is used to encode the smallest matrix dimension. We recently demonstrated how spatiotemporal encoding using the xSPEN technique can be applied to swap phase and frequency encoding dimensions [1] on this scanner. However, those scans suffered severe geometric distortions due to the lack of an xSPEN reconstruction that incorporates gradient non-linearity. Here we describe a model-based reconstruction method for these acquisitions that resolves these distortions and demonstrate it in phantom and in vivo imaging.Methods
Pulse Sequence and Imaging ExperimentsFigure 1b illustrates the scan geometry. On this scanner imaging is typically performed using frequency selective pulses that excite thick (2 cm) slabs that are subsequently frequency encoded using the built-in z-gradient, and phase-encoded using the pulsed x and y gradients. Here we implemented a multislice xSPEN acquisition that swaps the roles of the fixed z and pulsed y gradients, so that the time-efficient readout encodes the y dimension. The x dimension remained phase encoded. Figure 2 illustrates one shot of the xSPEN sequence, which uses WURST pulses for wideband adiabatic excitation (10 kHz bandwidth, 1.5 ms duration) and refocusing (20 kHz bandwidth, 1.65 ms (CHORUS) and 1.5 ms duration (echo train)). Gy trapezoids with opposite polarities were played during the first and second refocusing pulses for xSPEN encoding. The first refocusing pulse is 1.1x longer than the subsequent pulses to implement the CHORUS technique [2], wherein the first refocusing pulse compensates both the quadratic phase of the excitation and the first refocusing pulse, yielding a spin echo signal after the second refocusing pulse. Data were acquired with the sequence in an ACR phantom and a healthy male subject with IRB approval. The scans used TR 1.5 s, 4 averaged echoes per multi-echo ‘shot’, and 18 slices, for a total scan time of 15 minutes or 48 seconds per slice.
Signal Model and Image Reconstruction
Disregarding constant linear and zeroth order phase terms, the first and second WURST and Gy pulses establish a bilinear phase distribution across the Gy and z gradient dimensions, resulting in the xSPEN signal equation:
$$S(t)\propto\int_{\vec{x}}d\vec{x}\rho(\vec{x})\frac{2\pi{BW}_{ex}}{\gamma{G_z}(\vec{x})}sinc\left\{ \left(-C'(\vec{x})+t-T_a/2\right)\pi{BW}_{ex}\right\},$$
where $$$BWex$$$ is the excitation bandwidth, and $$$C'(x)$$$ is the bilinear xSPEN curvature. The sinc spatial encoding function in this equation sweeps the entire y-FOV each echo and is shown in Figure 3 for a central slice of the acquired in vivo volume. The equation was extended to include Gx phase encodings and was discretized to the acquired 75 time points per 1.5 ms-long xSPEN echo and the acquired 32 Gx phase encodes, and a system matrix was constructed using measured Gx and Gy gradient fields. The conjugate gradient algorithm implemented in SigPy [3] was run for 20 iterations with Tikhonov regularization to reconstruct images to 12 x 12 cm2 (ACR phantom)/18 x 18 cm2 (in vivo) image grids with a 64 x 64 matrix size.
Results
Figure 4 shows ACR phantom images reconstructed using a previously described naïve reconstruction in which the magnitude raw data were Fourier transformed in the xSPEN dimension and then reconstructed using a conventional inverse Fourier technique. The lack of non-linear gradient consideration in the forward Fourier transform resulted in severe geometric distortions which were alleviated by the direct model-based reconstruction. Figure 5 shows in vivo images reconstructed using the same two methods. The Fourier approach again produced geometric distortions relative to the model-based reconstruction, as well as vertical aliasing. In addition, the signal in the prostate was higher in the model-based reconstruction.Discussion
Future work on this acquisition will focus on reducing scan time while maximizing SNR. Presently the scan averages across the multiple echoes per train which share the same phase encoding; next we will apply differential phase encoding across echoes. SNR will be increased using a radial acquisition wherein the xSPEN and phase encoding [4] will both rotate between shots for a smaller FOV with higher resolution centered on the prostate, while maintaining the same time per readout to maximize signal averaging.Conclusion
xSPEN can be applied on a single-sided low-field MRI scanner with a built-in gradient field, to swap phase and frequency encoded axes so that the most time-efficient encoding mechanism can be leveraged for a large image matrix dimension. An analytic signal model was derived and implemented in a model-based image reconstruction that incorporated the scanner’s non-linear gradient fields, which yielded images free of distortions due to incomplete modeling of the xSPEN encoding process.Acknowledgements
No acknowledgement found.References
- M Gomes et al. Multiecho xSPEN for Single-Sided Low-Field MRI. ISMRM Low-Field MRI Workshop, 2022.
- J E Power et al. Increasing the quantitative bandwidth of NMR measurements. Chem. Commun., 52: 2916-2919, 2016.3.
- https://github.com/mikgroup/sigpy/
- Z Zhang et al. Phase-encoded xSPEN: A novel high-resolution volumetric alternative to RARE MRI. Magn Reson Med, 80:1492–1506, 2018.
Figures

Figure 1: (A) The single-sided prostate MRI scanner. The subject sits in lithotomy position and there is a hole in the magnet for surgical and biopsy access to the prostate. (B) The xSPEN imaging geometry. Slice-selection is performed along the magnet’s z-dimension, and the in-plane (x/y) dimensions are conventionally both phase-encoded. In this work, xSPEN is applied to swap the typically frequency encoded but small matrix dimension (z) with a typically phase-encoded but large matrix dimension (y), for faster imaging.
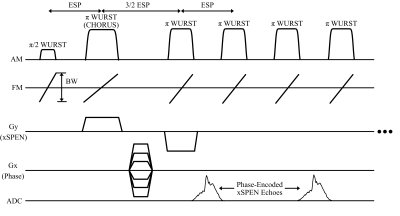
Figure 2: Phase-Encoded xSPEN imaging pulse sequence. Chirped WURST pulses are used throughout to excite and refocus the slice’s wide bandwidth. The first refocusing pulse is 1.1x longer than subsequent refocusing pulses to compensate both the subsequent pulse’s quadratic phase, and the excitation pulse’s quadratic phase, yielding a spin echo signal after the second refocusing pulse. This necessitates increasing the amplitude of the second Gy pulse to maintain the same amplitude-pulse duration product which sets the xSPEN bilinear curvature.
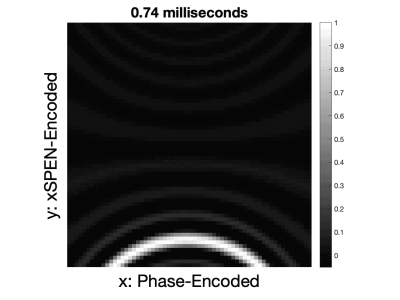
Figure 3: The xSPEN spatiotemporal encoding function as it moves along the y-direction during a 1.5 ms-long readout window in a central slice of the in vivo scan. The FOV here is 18 x 18 cm, and the x-dimension was phase encoded. The varying curvature is due to y-gradient non-linearity across the FOV.

Figure 4: Reconstructions of a center slice of a 10 cm-diameter ACR phantom. The left image was obtained via a Fourier reconstruction described previously [1]. The right image was obtained with the described model-based reconstruction which completely accounts for gradient non-linearity. The model-based reconstruction has significantly lower geometric distortions and more uniform signal inside the phantom.
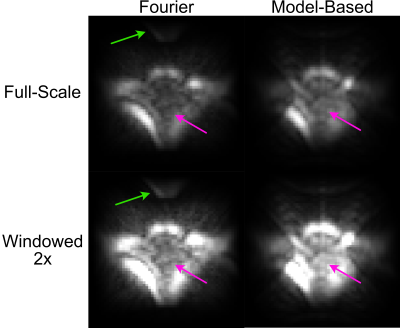
Figure 5: Reconstructions of a center slice of an in vivo prostate scan. The left image was obtained via a previously described Fourier reconstruction [1]. The right image was obtained with the model-based reconstruction which completely accounts for gradient non-linearity. The model-based reconstruction has higher signal in the prostate (purple arrow) while the Fourier reconstruction contains signal that aliased to the top of the image (green arrows) and is particularly visible in the 2x-windowed images in the bottom row.
DOI: https://doi.org/10.58530/2023/4623